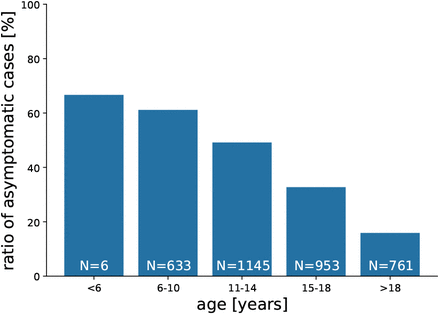Abstract
How to safely maintain schools open during a pandemic is still controversial. We aim to identify those measures that effectively control the spread of SARS-CoV-2 in schools. By control we mean that each source case infects less than one other person on average.
Here, we analyze Austrian data on 616 clusters involving 2,822 student-cases and 676 teacher-cases with the aim to calibrate an agent-based epidemiological model in terms of cluster size and transmission risk depending on age and clinical presentation. With this model, we quantify the impact of preventive measures such as room ventilation, reduction of class size, wearing of masks during lessons, and school entry testing by SARS-CoV2-antigen tests.
We find that 40% of all clusters involved no more than two cases, and 3% of the clusters only had more than 20 cases. The younger the students, the more likely we found asymptomatic cases and teachers as the source case of the in-school transmissions. Different school types require different combinations of measures to achieve control of the infection spreading: In primary schools, it is necessary to combine at least two of the afore-mentioned measures. In secondary schools, where contact networks of students and teachers become increasingly large and dense, a combination of three measures is needed. A sensitivity analysis indicated that the cluster size might increase up to three-fold in secondary schools for virus variants with an increased transmissibility by 50%, and that poorly executed or enforced mitigation measures might increase the cluster size by a factor of more than 30.
Our results suggest that school-type-specific combinations of measures, when strictly adhered to, allow for a controlled opening of schools even under sustained community transmission of SARS-CoV-2. However, large clusters might still occur on an infrequent, however, regular basis. It is shown explicitly that strict adherence to the measures is a necessary condition for successful control.
Main
Returning teachers and students to schools safely after lock-down periods during the COVID-19 pandemic requires a precise public health approach that is guided by evidence on the actual transmission dynamics in different types of schools, and a thorough evaluation of the effectiveness of different non-pharmaceutical interventions (NPIs) to prevent in-school-transmissions (1–4). Currently available evidence suggests a relatively low transmission of SARS-CoV-2 in schools (5–11), particularly among younger students (12–15). However, outbreaks with attack rates of up to 17% (16) have been reported particularly in secondary school settings and in regions with a high SARS-CoV-2 incidence in the community (17, 18). Strategies for safely re-opening schools therefore need to take the type and characteristics of a school and the epidemiological situation in its area into account.
Most countries are currently deploying a range of different NPIs to prevent transmissions in schools. Potential containment measures include wearing of masks (also inside class rooms), class size reductions through student cohorting, and room ventilation. With the emergence of new generations of antigen (AG) tests, at-home or self-testing is now also becoming feasible at scale and allows for novel screening strategies in schools to rapidly identify asymptomatic or presymptomatic cases of infection (19–21). Modelling studies suggest that the low sensitivity of AG tests, compared to PCR tests, can be offset by their short turnover time (the test result is available within minutes) and more frequent use (22).
To date there is limited evidence of how effective these measures or their combinations are to prevent transmissions in the different school types. Descriptions of clusters in schools are often limited to a handful of outbreaks (23–25) or do not reliably delineate in-school transmissions from out-school transmissions among school-aged children, which might have occurred in other settings like households (26). While sophisticated modelling approaches for the transmission dynamics in schools have been proposed (27–29), these models often lack the comprehensive and detailed information on a large number of school clusters that would be needed for a proper calibration and validation.
Here, we develop an agent-based model that is calibrated to Austrian data on school-clusters, in order to evaluate the effectiveness of combinations of NPIs in preventing transmission in five different school types: primary, lower secondary, upper secondary, secondary, with or without day care. A cluster is defined as a group of at least two cases of SARS-CoV-2 infection, which were epidemiologically linked as an infector (i.e. source case) and an infectee (i.e. successive case). A school cluster includes at least one infectee generated by in-school transmission. The source case of the in-school transmission(s), a teacher-source case or a student-source case, occurs in any other setting, such as household, work place, leisure activity, or in an unknown setting. For identifying the source case and successive cases, we used information on disease onset and possibly contagious interactions within 14 days prior to disease onset. These data derived from standardised case-interviews performed by the responsible public health authorities. For the model we included 616 clusters involving 2,822 student-cases and 676 teacher-cases that occurred between calendar weeks 36 and 45, in 2020. The model couples in-host viral dynamics with population dynamics taking place on contact networks determined by school type, number of classes, and average class size. These contact networks are time-dependent (students and teachers follow a weekday-specific schedule where contacts take place in classes, teacher facilities, during daycare, or between siblings in households) and multi-relational (transmission risks depend on intensity and type of contact). The viral dynamics allow for a more faithful representation of testing strategies. The probability of an exposed individual to transmit the disease, as well as the probability to be tested positive changes over the course of an infection and, additionally, depends on the presence of symptoms. The model is calibrated to actual Austrian cluster data to ensure that it reproduces realistic (i) cluster sizes, (ii) the ratio of infected teachers to infected students, (iii) the ratio of symptomatic to asymptomatic infected individuals, and (iv) the ratio of teacher-to-student source cases, and in addition, also the age-dependence of these observables.
Using the model, we study the effectiveness of four categories of NPIs and their combinations. These NPIs include (i) room ventilation, (ii) use of surgical masks of teachers and students during lessons, (iii) student cohorting, and (iv) screenings by use of entry AG tests for SARS-CoV-2 at different frequencies. As a reference scenario we consider a test-trace-isolate strategy in which students and teachers are PCR-tested as soon as they develop symptoms. We evaluate to which extent each of the aforementioned measures contributes separately to a reduction of cluster size with respect to the reference scenario. We then assess the combined effectiveness of NPI bundles and the sensitivity of our results with respect to the stringency of implementing these measures. We further investigate the impact of a more transmissible strain. Our aim is to quantify how many transmissions can be expected for the different scenarios in the different school types, in a way that is appropriate to derive evidence-based policies for keeping schools open at a controllable infection transmission risk.
Results
A. Cluster analysis
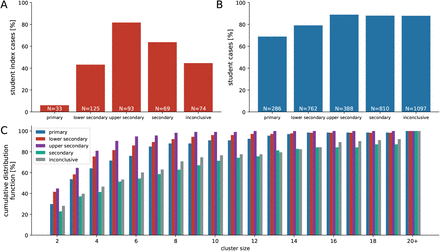
We identified 616 clusters including at least one in-school transmission. In total, these clusters involved 9,232 cases. Out of these, 2,822 were student-cases and 676 teacher-cases, of which 464 were source cases (introduced the virus into the school setting) and 3034 cases were generated by in-school transmission. In total, 286 cases were related to primary schools (69% students), 762 to lower secondary schools (79% students), 388 to the upper secondary schools (89% students) and 810 to the secondary schools (88% students), see also Figure 1 B. The portion of student-source cases was lowest in primary schools (6%), followed by lower secondary (43%), secondary (64%) and upper secondary (82%), see Figure 1 A. The average size (i.e. number of cluster cases) of clusters with a teacher as source case (5.7 cases) was larger than that of clusters with students as source (4.4 cases). The clinical presentation was clearly age-dependent. While 4 out of 6 students younger than 6 years old were asymptomatic, the proportion of asymptomatic cases dropped by increasing age from 61%, 49%, 33% and 16% for the age groups 6–10, 11–14, 15–18 and adults (including students and teachers), respectively. Figure 1 C shows the distribution of cluster size by different school types. Overall, cluster sizes of 2, 3–9, 10–19 and 20+ cases accounted for 40%, 49%, 8% and 3%, respectively.
Cluster data for transmissions in schools. The ratio of A student-to-teacher source cases is lower in school types with young children (primary, lower secondary) and higher in school types with older children (upper secondary, secondary). The same trend is seen in the proportion of students in clusters B. C The cumulative distribution function of cluster sizes shows a majority of clusters consisting of only a handful of cases, whereas clusters with 20 or more cases still do occur, particularly in (upper) secondary schools.
B. Model calibration
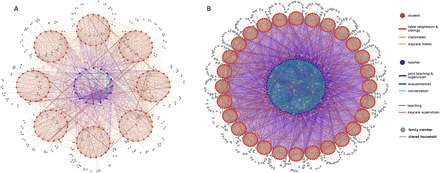
We depict two exemplary contact networks for the typical Austrian primary and secondary school types in Figure 2. There we observe that contact networks vary substantially between primary and secondary schools, the latter showing larger and denser networks. Increased network density is driven by teachers playing a more relevant role as link between classes in secondary schools due to differences in the structure of curricula. In secondary schools, teachers often change between class rooms during the day whereas in primary schools they typically supervise only one class. To reproduce the empirically observed cluster characteristics, we find a transmission risk for “intermediate contacts” (e.g., table neighbors in a school class, thick red lines in Figure 2) compared with household contacts by 15% lower and for “loose” contacts (e.g., shared classroom but not table neighbors, thin red lines) a transmission risk by 25% less. See also Table 3 for contact classifications. Students younger than 18 years old have a transmission risk that is reduced by 0.02(18−y)%, where y is age. We use this optimal parameter combination for all subsequent simulations to analyze the effect of different prevention strategies on characteristics of clusters in schools.
Contact networks of agents in schools. A representative Austrian primary school with afternoon daycare, including 8 classes with 19 students each, 16 teachers, and their respective family members. B Typical Austrian secondary school, including 28 classes with 24 students each, 70 teachers, and their respective family members. Contacts between students (red circles) are depicted in shades of red and include contacts between table neighbours, class mates, students in the same daycare supervision group and siblings. Contacts between teachers (blue circles) are depicted in shades of blue and include contacts between teachers that teach or supervise together, short conversations and acquaintances. Contacts between household members (grey circles) are depicted as grey lines. Contacts between teachers and students that arise during teaching or daycare supervision are depicted as purple and pink lines.
C. Effectiveness of measures
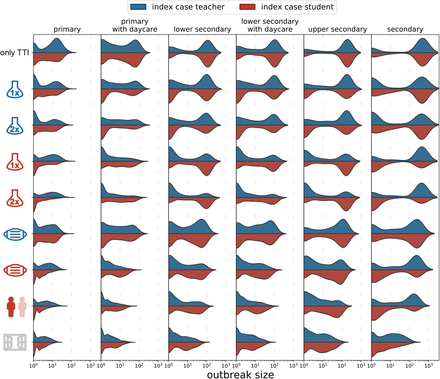
Results for the effectiveness of individual measures are shown in Figure 3 in terms of the distributions of cluster sizes with students or teachers as source cases. In Supplementary Information (SI) Table 1, we show the average cluster size along with the 75th and 90th percentile, and the reproduction number, R, of clusters with students and teachers as source cases, respectively. If R < 1, we consider a cluster in a given scenario as “controlled”. See Methods Section L for the calculation and interpretation of R.
Distributions of cluster sizes for different school types (columns) and measures (rows) with teachers (blue) or students (red) as the source cases. Results are shown for only test-trace-isolate (TTI) as baseline and TTI plus an individual measure (testing teachers/students once or twice a week, teachers or students wearing masks during the lessons, class size reductions, ventilation), respectively.
We consider a “no mitigation” scenario in which no preventive measures except diagnostic testing and screening in the event of a symptomatic case (see Methods Section J.3) are enacted, as reference. This assumption results in a bimodal distribution of the cluster size containing small clusters of ten or less cases and large cluster with up to hundred cases or more in secondary schools. Assuming average school sizes of 152, 144, 230 and 674 students for primary, lower secondary, upper secondary and secondary schools (30), on average we find 8 cases per cluster in primary schools (75th percentile: 20 cases, 90th percentile: 36), 57 (172, 192) cases in lower secondary schools and 282 (746, 806) cases per cluster in secondary schools, overall. For each school type the average reproduction number is larger than one, ranging from 1.8 (standard deviation 1.7) in primary schools, and 2.6 (SD 2.2) in lower secondary schools to 3.4 (SD 2.6) in secondary schools if the source is a student. Clusters with teachers as source case are typically larger and show higher reproduction numbers, ranging from 3.4 (SD 3.0) in primary, 6.5 (SD 5.5) in lower secondary to 8.6 (SD 7.9) in secondary schools.
Considering each measure separately, we see the largest reduction in cluster size for room ventilation. Room ventilation diminishes the size of student-source clusters to 2 (4, 6) cases on average in primary schools, to 5 (8, 22) cases in lower secondary schools and to 9 (13, 32) cases in secondary schools. For teachers as source cases, cluster sizes are reduced to 3 (6, 10) in primary schools, 8 (16, 34) in lower secondary and 16 (32, 66) in secondary schools.
Class size reductions have the second biggest impact, with 2 (4, 6) cases in primary, 9 (16, 46) in lower secondary and 34 (22, 220) in secondary schools for students as source cases. For clusters with teacher as the source case, the cluster sizes are reduced to 4 (8, 12) cases in primary, 17 (38, 68) cases in lower secondary and 81 (220, 278) in secondary schools.
If students wear masks, the cluster sizes are reduced to 2 (4, 8) cases in primary, 13 (26, 76) in lower secondary and 60 (180, 360) in secondary schools with students as source cases. Clusters with a teacher source case are up to twice as large as those that originate from students, on average. If only the teachers wear masks, cluster sizes with students as the source cases are reduced to 5 (14, 22) cases in primary, 24 (65, 108) in lower secondary, and 109 (344, 478) in secondary schools.
Screening by means of active case finding through AG testing reduce cluster sizes, but not as much as room ventilation, class size reductions or mouth-nose mask-usage. Testing students twice a week reduces the cluster size to 3 (4, 12) cases in primary, 41 (126, 168) in lower secondary and 107 (484, 680) in secondary schools when students are the source case and to 8 (20, 34) in primary, 49 (145, 178) in lower secondary, and 248 (659, 736) in secondary schools for teachers as source case. Testing teachers twice a week reduces cluster size, particularly for teacher-source clusters to 6 (14, 30) in primary, 30 (100, 160) in lower secondary and 161 (596, 702) in secondary schools. For students as source case, the cluster sizes are reduced to 6 (14, 24) in primary, 41 (126, 168) in lower secondary and 188 (638, 710) in secondary schools.
Except for the measures room ventilation, class size reduction, mask-usage among students and 2-times testing among students, the average reproduction number for student-source clusters remains above one in primary schools, in case of implementing a single measure. Control of SARS-CoV-2 spread in schools by means of R < 1 requires a combination of preventive measures.
D. Combination of measures
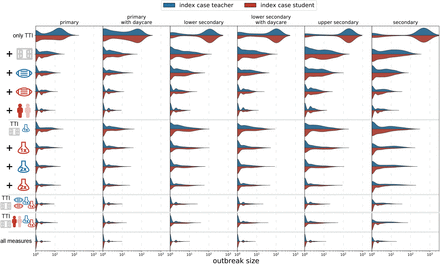
Results for selected combinations of preventive measures are shown in Figure 4 and Table 2.
Distribution of cluster sizes as in Figure 3 for combinations of measures. From top to bottom, we first consider only test-trace-isolate (TTI) (first row) plus ventilation (second row). We then evaluate the combination of TTI and ventilation with masks for teachers, masks for students, as well as class size reductions. Next, we evaluate the combination of TTI and ventilation with test screenings amongst teachers and students once or twice per week. Cluster sizes are even further reduced for measure combinations that combine ventilation and testing with masks or class size reductions. Finally, we evaluate the combination of all of the above measures.
We first consider combinations, in which we sequentially combine NPIs in the following order: room ventilation, mask usage by teachers, mask usage by students, and class size reduction. This roughly corresponds to an increasing complexity and cost of measure implementation in practice. In primary schools, R drops below one with room ventilation and mask usage by teachers with cluster sizes of 2 (4, 6) and 2 (2, 6) for student- and teacher-source cases, respectively. In primary schools with day care, also mask-usage by students is required to achieve R < 1 and to reduce the size of clusters with student-source case from 23 cases (73, 116) to 1 (2, 4). For all other school types (lower/upper secondary, with or without day care), in general also class size reduction is necessary to achieve R < 1. However, large clusters become increasingly rare even with room ventilation and mask-wearing only, with 10% of clusters resulting in 8 or more cases in (upper) secondary schools, and 6 or more cases in lower secondary schools, with or without day care.
When looking at combinations of measures including room ventilation together with different preventive test strategies in primary schools, ventilation and testing teachers once a week by AG tests achieves R < 1 for teachers and students as source case. In primary schools with day care, also testing students once per week is required to achieve R < 1. In lower secondary schools, clusters with a student-source case can be reduced to an average cluster size of 2 (4, 8) by testing students and teachers once a week. For teachers as the source case, testing students and teachers twice a week still results in R = 1.4 (SD 2.1) with an average cluster size of 3 (6, 12). Similar results hold for the other types of secondary schools. Controlling clusters which originate from students can be achieved through weekly testing for SARS-CoV-2 infection. However, 10% of clusters remain above 8 (lower secondary with day care) and 12 cases (upper secondary, secondary schools), respectively. Clusters originating from teachers show an average R > 1 for all analysed testing strategies in combination with room ventilation, e.g., cluster size of 6 (8, 26) cases in secondary schools with R = 2.0 (SD 2.9).
Room ventilation and weekly AG testing combined with mask-usage result in spread control of clusters with a teacher-source case in all school types. The average cluster size is below 2 in all school types and for each source case. Ten percent of clusters with teacher source case in secondary schools have more than 6 cases (4 in secondary, 2 in primary schools). Combining ventilation and testing with class size reduction shows a smaller size reduction compared to mask-usage, e.g., with an average cluster size of 4 (4, 12) and R = 1.5 (SD 2.2) for clusters with a teacher-source case in secondary schools. Combining all aforementioned NPIs results in R < 1 for all school types and both types of cluster source-case. In secondary schools, 10% of clusters occur with more than 2 cases despite the combination of the NPIs.
E. Sensitivity analysis and conservative estimates
The effectiveness of every preventive measure depends on the implementation in practice. To assess the varying efficiency of measures in practice, we systematically vary the parameters of the measures in the simulations and compare the resulting cluster sizes to the cluster sizes of the “baseline” scenarios shown in Figure 4. Regarding the efficiency of screening for SARS-CoV-2 infection among asymptomatic students and teachers by AG testing, we vary the sensitivity between 10% and 90%, the proportion of teachers and students participating voluntarily in testing between 10% and 90% of the agent population and the proportion of students staying at home when class sizes are reduced between 10% and 70% in each class. We vary the transmission risk reduction that can be achieved by room ventilation between 20% and 90% and the reduction associated with mask-usage between 30%, [10%] and 90% [70%] for exhaling [inhaling].
To illustrate the combination of the different efficiencies of the measures of interest, we assume a “worst case” scenario with conservative estimates for the parameters. Thus, we consider a sensitivity of 40% for the AG test (as compared to 100% in the optimal scenario, see also Methods Section J.3), a participation of teachers and students in AG testing of 50% (as compared to 100% in the optimal scenario). This small proportion of participating persons may reflect the phenomenon of increased “COVID skepticism” and the concerns voiced by parents about their children being tested at school1. Furthermore, we consider for class size reduction, that 30% of students stay at home (compared to the targeted 50%). In order to reflect the uncertainty of room ventilation on reduction of aerosols, we consider a transmission risk reduction of 20% (as compared to 64% in the optimal scenario), see for example Curtius et al. 2021 (31), Sun and Zhai (32), Lelieveld et al. 2020 (33). Finally, we consider mask-wearing to be associated with a transmission risk reduction of 40% and 20% for exhaling and inhaling, respectively (as compared to 50% and 30%, respectively, in case of optimal mask efficiency). In summary, these estimates represent informed guesses, as to date there are no reliable data available to assess these parameters.
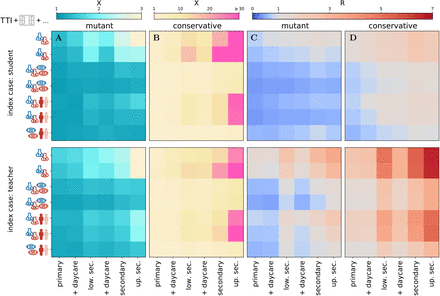
The results of this sensitivity analysis, in addition to the average number of transmissions of the source case R, are reported with the “fold-increase”, X, i.e., the factor by which the average cluster size of a given scenario is increased with respect to the average cluster size of the baseline scenario (given in SI Table 2). Results are shown in Figure 5 (columns B and D) for the same measure combinations that we assessed in Figure 4. We assess the varying efficiency of a single measure in the SI (Figure 1).
Fold increase of the average cluster size with respect to the results shown in Figure 4, X, in panels A and B. Panels C and D) show the respective change in R. The panels A and C show the situation for variant with a 50% increased transmissibility. Conservative estimates for the effectiveness of measure implementation are seen in panels B and D. Results are shown for student source cases (top) and teacher source cases (bottom) for each measure package (row) and school type (column).
In all scenarios, the reduced effectiveness of the preventive measures leads to an exponential increase of the cluster size. Therefore, we conclude that our simulated system is highly sensitive to the assumed differences in the efficiency of these measures. The extent of increase in the cluster sizes is comparable for student and teacher causing school clusters. In brief, our results show that preventive strategies that focus on testing only (next to ventilation, which is present in all strategies), while assuming conservative assumptions (proportion of participants and test sensitivity), is associated with the largest increase in cluster size, regardless of school type and school cluster source (teacher or student). We observe a more than 40-fold increase in the infection risk in upper secondary and secondary schools, an almost tenfold increase in lower secondary schools and a threefold increase in infection risk in primary schools. A preventive strategy that combines testing (2x) with class size reduction shows an increase of the average cluster size of two-times in primary schools, eight-times in lower secondary schools and 27-times in secondary schools for clusters with students as the source case. Preventive strategies that combine mask-wearing with either testing or reduced class sizes show smaller increases in infection risk ranging from 1.7-to 8-fold and 1.3-to 3.1-fold, respectively.
F. Variants with increased transmissibility
In Figure 5 (panels A and C), we illustrate the effectiveness of combinations of measures with varying performances considering a virus variant with a 50% increased transmissibility. This increase in transmissibility reflects the current estimates of the transmissibility increase of the currently most prevalent SARS-CoV-2 strain B.1.1.7 (34) with respect to the earlier dominant variant. Again, we find similar cluster size increases for both types of source cases. The preventive strategies that only combine room ventilation with testing show the largest increases of clusters with student source case in secondary schools being 3.0-fold (testing once a week) or 2.3-fold (twice a week) larger compared to the previous variant. Compared to the conservative estimates, the ranking in terms of risk increase has neither changed for the different combinations of measures (largest increases for preventive screening only and preventive screening combined with class size reductions), nor for the school types (smallest risk increase for primary schools, largest increase for upper secondary schools).
G. Online visualization
To allow the concerned parties (i.e., school administrative staff, parents, as well as students) to investigate the effect of measures on their specific school setting, we created an online simulation viewer2 as an interactive interface to our study results. The tool allows users to configure a school in terms of the school type (see SI Section 1), class size (i.e., average number of students), number of classrooms, and number of floors. Based on their configuration, users receive an overview of the effect of measures on their schools in terms of cluster size and resulting quarantine days (see Methods Figure 9). Individual measure configurations can then be selected to display an animation that illustrates a representative cluster development in the school over time (see Methods Figure 10).
Discussion
We analyzed Austrian data on 616 SARS-CoV-2 clusters with at least one in-school transmission. We used this data to calibrate a detailed agent-based epidemiological model that quantifies the effectiveness of combinations of preventive measures across different school types for student-source cases and teacher-source cases. Different types of schools require different preventive measures to control the spread of SARS-CoV-2. As any single measure (mask-wearing, room ventilation, school entry testing, class size reduction) is typically not enough to achieve control (R < 1), the school management needs to think in terms of smart combinations of measures to safely operate schools in the COVID-19 pandemic.
Current evidence suggests that schools mirror the infection dynamics observed in the general population (17, 18), though it seems that smaller children typically contribute less to virus spread (12–15). In line with these findings, we find that the setting-specific reproduction number for clusters with teachers as source case increases from around 3 for primary schools to more than 8 for secondary schools in a scenario with TTI only, whereas for students as source case the reproduction numbers range between 2 and 3. Secondary schools are therefore a riskier transmission setting, particularly if a contagious teacher is present. Keeping schools open in a controlled way in regions with sustained community transmission is therefore only feasible if stringent mitigation measures are put in place and are strictly adhered to.
We find two main reasons for the differences between primary and secondary schools. Even if we assume viral load in children to be comparable to adults, the less coughing, smaller lung volume, and the emission of aerosols from a lower height with suspension in the air for a shorter duration of time, suggest that transmission risk increases with age in children. Indeed, our calibrated model yields that the risk for transmission increases by about 25% upon contact with a six year old person compared to a contact with an 18 year old person. Further, and more importantly, secondary schools have contact networks of a completely different structure (see Figure 2 for a comparison between a primary and a secondary school). In Austria, the average secondary school has 28 classes with 24 students each and a total of 70 teachers, whereas primary schools have 8 classes with 19 students each and 16 teachers in total. Typically teachers in secondary schools often change between class rooms during a day, whereas primary school teachers typically supervise only one class. Hence, contact networks in secondary schools are both denser and larger than in primary schools, which together with the age dependence of the transmission rates, leads to the observed differences in cluster sizes.
In line with the cluster data, we also find that clusters with teachers as the source result, on average, in larger number of successive cases than clusters originated from students. There are multiple reasons for this increased transmission risk for infected teachers. First, teachers have to speak loudly facing all students for a substantial amount of time. Second, particularly in primary schools they contribute more to the spread due the age dependence of the transmission risk. Third, particularly in secondary schools they have a higher degree in the contact network, since teachers visit more classes per day as compared to primary schools. Mitigation measures that target teachers are therefore a necessary prerequisite to control the spread of SARS-CoV-2 in schools.
Here we analyzed four types of mitigation measures, namely (i) requirements to wear face masks during lessons, (ii) room ventilation, (iii) class size reduction, and (iv) screening for SARS-CoV-2 infection in asymptomatic students and teachers by means of antigen testing. We find that each of these measures by itself contributes to curbing the virus spread, but particularly in secondary schools or in schools with day care large clusters are still likely to occur regularly, unless several measures are combined. The most effective measures in terms of reducing cluster size is room ventilation, followed by class size reductions, mask-wearing, and entry testing. In primary schools, in general it is necessary to combine at least two of these measures to reduce the reproduction number below 1, whereas in (lower or upper) secondary schools and secondary schools it is necessary to combine at least three measures.
The effectiveness of each measure in terms of cluster size reduction depends on how well it can be implemented in practice. We found that linear decreases in measures’ efficiency (e.g., participation ratios in class size reductions or testing) translate into exponential increases in cluster sizes. Therefore, a more stringently and consistently implemented measure might outperform even a measure that would be more effective under ideal circumstances. Means and incentives to ensure the proper implementation of each measure in practice are the key to success. For instance, a negative SARS-CoV-2-test result could be made mandatory to be allowed to attend school, or class rooms could be equipped with CO2 sensors to ensure a proper room ventilation regime. Such “enforced” measures are to be preferred with respect to theoretically more effective measures that cannot be controlled, e.g., class size reductions if a substantial part of the students still visits the school (or a care facility) on each day of the week due to work obligations of the parents.
We are facing an increasing number of SARS-CoV-2-virus variants with increased transmissibility compared to the former types (34), which makes it necessary to constantly reevaluate mitigation measures. Here, we consider a virus variant with an increased tranmissibililty of 50% and find that for many combinations of measures, cluster sizes might increase by a factor of three in secondary schools, whereas the increase in primary schools are rather modest. Not diminishing the risk associated with more transmissible variants, it is still striking that the difference between a well and not-so-well implemented preventive strategy may be larger than the difference between the virus variant being 50% more transmissible or not. This further underscores the importance of relying on a mitigation strategy consisting of multiple prevention measures accompanied with means and incentives to ensure the proper implementation of these measures.
H. Limitations of the study
Our work is subject to several limitations, pertaining both to the observational cluster data our calibration relies on, as well as to simplifications employed in the model.
The issue of age-dependent transmission risk is currently controversially discussed (see for example Anastassopoulou et al. 2020 (35)). The transmission dynamics can be attributed to information bias, due to a higher share of asymptomatic cases in children – or to a mix of information bias and true decreased transmission risk among children. Our data clearly confirms that the probability for asymptomatic courses of the infection decreases with age (see Figure 8). TTI strategies are typically triggered by the occurrence of a symptomatic case. Cluster cases might have been missed because not all contacts of the cases have been tested for infection. Since adults with a SARS-CoV-2 infection are more likely to develop symptoms and therefore to be tested, source cases might have been identified over-proportionally among teachers than among students. This might result in missed instances of student-to-student and student-to-teacher transmissions. The data on which our calibration is based upon represents a time at which the social environment of confirmed positive cases was stringently tested by the Austrian authorities. Specifically, authorities tested both category 1 and category 2 contact persons without discriminating between symptomatic and asymptomatic presentation. Nevertheless, we recognize that due to an increasing strain on the testing and tracing resources in some periods, this protocol might have been modified to some extent to preferentially test symptomatic cases. It is not possible for us to assess to which extent this might have been the case and we recognize this as a limitation of our study. As a result, the (small) decrease of transmission risk for younger children that results from our calibration could be influenced by observational biases in the empirical data. Based on the aforementioned limitations our calibration results that children infected with SARS-CoV-2 are less contagious need to be interpreted with caution.
The agent-based model is limited with respect to a number of aspects concerning both the simulation itself as well as the underlying contact networks. Firstly, to limit computational cost, we chose a rather coarse time resolution for the simulation (1 day). This can lead to a simplified representation of the infection dynamics, especially in the early days of an infection, when viral load increases approximately exponentially. Nevertheless, since epidemiological parameters controlling infection dynamics are themselves drawn from distributions, the coarse time resolution should not lead to any artifacts, for example in interaction with timed measures (weekly screening). Secondly, we limit possible contacts between agents in the model to a set of the most frequent interactions arising in the school context between the predominant types of agents. We ignore other interactions and agent types, such as contacts between students in school busses or on hallways, or other personnel, such as janitors. These interactions are assumed to be less frequent and less relevant than the interactions represented in the model as schools go to great lengths to limit interactions between students of different classes. Furthermore, there is no available data on these contact types, which would render modelling them to guesswork. Lastly, we base many of our parameter choices, especially the estimates of the effectiveness of NPIs, on preliminary literature. With the sensitivity analysis of measure effectiveness included in this study, we try to cover different plausible scenarios. Nevertheless these estimates remain a source of uncertainty in the model.
Conclusion
In conclusion, we find that different types of schools require different combinations of preventive measures. The ideal mix of mitigation measures needs to be more stringent in secondary schools than in primary schools, and needs to preferentially focus on teachers as sources of infection. Even under strict prevention measures, larger clusters in schools will still occur at regular intervals when the incidence in the general population is high enough. However, in this work we have shown that keeping schools open during the COVID-19 pandemic a calculable risk can be achieved by a combination of stringently enforced measures.
Data and Methods
l. Empirical observations of SARS-CoV-2 clusters in Austrian schools
Clusters of Austrian SARS-CoV-2 cases are identified at the Agency for Health and Food Safety (AGES). Clusters of SARS-CoV-2 cases among Austrian residents are identified at the Agency for Health and Food Safety (AGES) in cooperation with the responsible public health authorities. A cluster is defined as a group of at least two cases of a confirmed SARS-CoV-2 infection, which are epidemiologically linked by means of an infector and infectee (i.e. successive case). A “school cluster” includes at least one case generated by in-school transmission. The source of a school cluster introduces the virus into the school setting, is either a teacher-case or a student-case, and is generated by out-school transmission, in settings such as household, work place, leisure activity, or in an unknown setting (referred to as teacher-source case or student-source case throughout the entire text, could be denoted as index case elsewhere).
As of December 22nd 2020, we identified 616 clusters with at least one school transmission with a starting date between calendar week 36 and 45, 2020. The starting date of a school cluster is defined as the date of laboratory diagnosis of its source case. The 616 clusters involved 9,232 cases. Out of these, 3498 were school cluster cases, including 2,822 student-cases and 676 teacher-cases. Out of the school cluster cases, 464 were source cases and 3034 cases were generated by in-school transmission. Each cluster was assigned to one of the school-types primary, lower secondary, upper secondary, secondary and inconclusive. Data on the exact school type was not available at the time of our analysis, therefore we assigned the clusters based on the age of students using the following algorithm:
primary: the age of all affected students is ≤ 10 years.
lower secondary: the age of all affected students is within the interval [10, 15] years.
upper secondary: the age of all affected students is ≥ 15 years.
secondary: the age of all affected students is ≥ 10 years.
inconclusive: otherwise.
n total, 286 cases were related to primary schools (69% students), 762 to lower secondary schools (79% students), 388 to the upper secondary schools (89% students) and 810 to the secondary schools (88% students), see also Figure 1 B. The share of student-source cases was lowest in primary schools (6%), followed by lower secondary (43%), secondary (64%) and upper secondary (82%), see Figure 1 A. The clinical presentation was clearly age-dependent. While 4 out of 6 students younger than 6 years old were asymptomatic, the proportion of asymptomatic cases dropped by increasing age from 61%, 49%, 33% and 16% for the age groups 6-–10, 11-–14, 15-–18 and adults (including students and teachers), respectively. Figure 1 C shows the distribution of cluster size among different school types. Overall, the amount of clusters with size 2, 3—9, 10-–19 and 20+ was 40%, 49%, 8% and 3%, respectively.
J. Agent-based simulation
J.1. Model
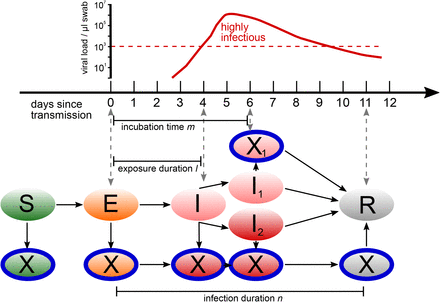
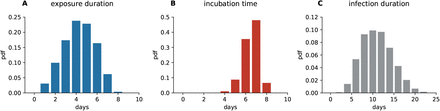
We simulate the infection dynamics in schools using an agent-based model (36). The model includes three types of agents, students, teachers, and their household members. The model couples in-host viral dynamics with population dynamics. Depending on the viral load over the course of an infection, each agent is in one of five states: susceptible (S), exposed (E), infectious (I), recovered (R) or quarantined (X) (see Figure 6). In addition, after the presymptomatic phase, agents can stay asymptomatic (I1) or develop symptoms (I2). Age also influences the transmission risk (see Section J.2 below). Agents remain in these states for variable time periods. Every agent has an individual exposure duration, l, incubation time (i.e., time until they may show symptoms), m, and infection duration, n (i.e., time from exposure until an agent ceases to be infectious), as depicted in Figure 6. For every agent, we draw values for l, m, and n from previously reported distributions of these epidemiological parameters for SARS-CoV-2. Exposure duration, l, is distributed according to a Weibull distribution with a mean of 5.0 ± 1.9 days (37–39). Incubation time, m, is distributed according to a Weibull distribution with a mean of 6.4 ± 0.8 days (40, 41), with the additional constraint of m ≥ l. Infection duration, n, is distributed according to a Weibull distribution with a mean of 10.9 ± 4.0 days (42, 43), with the additional constraint of n > l. Distributions are shown in Figure 7. Infections are introduced to the school setting through a single source case that can either be a student or a teacher. The source case starts in the exposed state on day 0 of the simulation. All other agents start in the susceptible state.
Agents in the epidemiological model can be in the states (ellipses) susceptible (S), exposed (E), infectious (I), infectious without symptoms (I1), infectious with symptoms (I2) and recovered (R). Possible state transitions are shown by arrows. In each of these states, agents can also be quarantined (X), preventing them from interacting with other agents. Transitions between states follow the development of the viral load in the host sketched above.
Distributions of parameters used in the agent based simulation. A exposure duration, l, B incubation time, m, and C infection duration, n.
Agents interact by means of networks of contacts specific to the school setting and the day of the week (see Section J.4 below). At every step (day) of the simulation, agents interact with other agents in the neighborhood of their day-specific contact network. Infected agents can transmit an infection to susceptible agents, unless one of them is quarantined. Quarantined agents are represented by isolated nodes in the contact network.
J.2. Transmission risk
During every interaction, an infected agent can transmit the infection to the agents they are in contact with (specified by the contact network, see Section J.4). Transmission is modelled as a Bernoulli trial with a probability of success, p. This probability is modified by several intervention measures and biological mechanisms qi, where i labels the measure or mechanism. Here, we consider eight such mechanisms (see Table 1 for details). This includes the modification of the transmission risk due to the type of contact between agents (represented by q1), due to the age of the transmitting and receiving agents (q2 and q3, respectively), the infection progression (q4), having or not having symptoms (q5), mask wearing of the transmitting and receiving agent (q6 and q7, respectively), and room ventilation (q8). Therefore, the probability of a successful transmission is given by the base transmission risk, β, of a contact and the combined effect of these eight interventions measures or biological mechanisms,
Mechanisms qi that modify the probability of a successful transmission, p, between agents. Values for the respective modifications are either calibrated using data of clusters that occurred in Austrian schools or taken from literature.
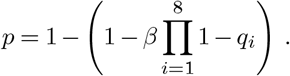 The base transmission risk β is calibrated with given empirical observations of actual clusters in the school setting (see Section K).
The base transmission risk β is calibrated with given empirical observations of actual clusters in the school setting (see Section K).
To model the reduction of transmission risk due to the type of contact between agents, we classify contacts into three categories. “Close” contacts are characterised by very long and physically very close interactions and occur only between members of the same household. “Intermediate” contacts are characterised by long and/or physically close interactions, for example between students sharing a table in the classroom. “Loose” contacts are characterised by short and more distant interactions, for example between teachers that have a short conversation in the coffee kitchen during a break. We model the reduction of the transmission risk, q1, for the contact types “intermediate” and “loose” as compared to the contact type “close”, which is calibrated given the risk of transmission in household settings (see Section K).
Infection dynamics of SARS-CoV-2 differs between children and adults (13, 14). There is still uncertainty concerning how individual biological or epidemiological factors impact the transmission of and susceptibility to an infection with SARS-CoV-2 in children. Susceptibility in children is believed to be inhibited due to a lower number of ACE2 receptors (44) that are necessary for the virus to enter cells. Transmission is believed to be inhibited due to the lower number of symptomatic cases in children (13) and their smaller lung volumes, which reduces the amount of virus-laden aerosols emitted by infected children (45). Yet, an accurate quantification of these effects still eludes us.
Here, to reduce the number of parameters that need to be calibrated we assume that both, reduced transmission and reduced susceptibility in children, contribute equally. We model both effects as a linear decrease of risk depending on the age of the student. The modification of the transmission risk due to the age of the transmitting agent q2 is modelled as a linear decrease of the infection risk with every year an agent is younger than 18,
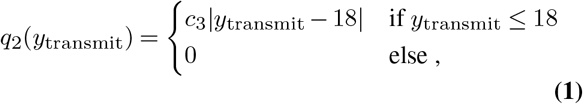 where ytransmit is the age of the transmitting agent and c3 is the slope of the linear relationship that is calibrated using empirical observations of clusters in the school setting (see Section K below). The modification of the transmission risk due to the age of the contracting agent q3 is also modelled as a linear decrease of the infection risk with every year an agent is younger than 18, using the same slope c3,
where ytransmit is the age of the transmitting agent and c3 is the slope of the linear relationship that is calibrated using empirical observations of clusters in the school setting (see Section K below). The modification of the transmission risk due to the age of the contracting agent q3 is also modelled as a linear decrease of the infection risk with every year an agent is younger than 18, using the same slope c3,
 where ycontract is the age of the contracting agent.
where ycontract is the age of the contracting agent.
The modification of transmission risk due to a changing viral load over the course of an infection, q4, is modelled as a trapezoid function that depends on the time an agent has already been exposed to the virus, t, given the exposure duration, l, incubation time, m, and infection duration, n, of the infected agent:
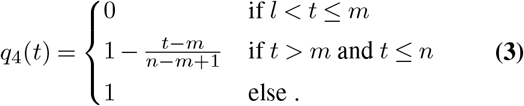 This means that the transmission risk is constant and high during the first few days after the exposure phase and until symptoms occur (in symptomatic agents), and then decreases linearly until the end of infectiousness is reached. This development is in line with recent investigations of the development of the viral load in patients infected with SARS-CoV2 (40, 42).
This means that the transmission risk is constant and high during the first few days after the exposure phase and until symptoms occur (in symptomatic agents), and then decreases linearly until the end of infectiousness is reached. This development is in line with recent investigations of the development of the viral load in patients infected with SARS-CoV2 (40, 42).
The reduction of the transmission risk due to not having symptoms q5 (46), wearing a mask q6 and q7 (47), and ventilating the room q8 (33), is modelled using literature values for the respective effects (see Table 1).
J.3. Testing and tracing
In all simulations, upon first developing symptoms, agents are immediately quarantined and tested with a PCR test that has a one-day result turnover time in the calibration scenario and a two-day result turnover time in every other scenario. This reflects the situation that during the time period from which our calibration data stems, testing and tracing was still sufficiently functional, while with increasing case numbers in late autumn 2020, the testing and tracing capacity reached its limits and delays increased. We gathered this information on typical test turnover times in our stakeholder interviews, described in M. In addition to testing of symptomatic agents (diagnostic testing), a positive diagnostic test result will initiate a test of all teachers and students in the school (background screen). Diagnostic testing, background screening and quarantining of contact persons (test–trace–isolate, TTI) occur in every scenario, even if no additional measures are implemented.
An additional preventive measure is screening testing, which intends to identify infected people who are asymptomatic and do not have known, suspected, or reported exposure to SARS-CoV-2. Screening tests can be performed in defined intervals. When screening tests occur once per week, it is performed every Monday, when twice a week then every Monday and Thursday. AG test for screening is the current practice in Austria. These tests have a same-day result turnover, reflecting the fact that results are usually available within minutes after the test.
The sensitivity of AG tests depends on the viral load of the swabs (22, 48). Therefore, the sensitivity of AG tests might depend on both, the clinical presentation of the disease, as well as the number of days a patient has been infected at the time of testing. The Austrian Agency for Health and Food Safety (AGES) validated the performance of AG test with the anterior nasal sampling (NS) and found a sensitivity of 40.7% among asymptomatic infected persons and of 75.9% in mildly symptomatic infected (49). The high sensitivity for mildly symptomatic patients is consistent with other studies that report sensitivity for symptomatic patients (50, 51). To date, there are no other reports for the sensitivity in asymptomatic patients and no study stratified the reported results by the time the patients had been infected. To account for the dependence of the sensitivity of AG tests on the viral load of the patients, we approximate the sensitivity by a step-function: in our model, the sensitivity of AG tests is 1.0 during a restricted time window between 6 and 11 days after exposure and 0 otherwise. We do not differentiate between agents with symptomatic and asymptomatic courses. Under the assumption that the likelihood of being tested within the scope of screening by use of AG tests is uniformly distributed over the entire course of the infection and with a mean infection duration of 10.9 days (42, 43), this results in an overall sensitivity of AG tests of 0.55 in our model. Therefore, the AG test sensitivity used in our model lies in between the sensitivities that were reported for asymptomatic (40.7%) and mildly symptomatic (75.9%) patients for the AG tests used in the school context in Austria (49).
PCR tests are very sensitive and require low numbers of virus copies in clinical samples to successfully detect an infection with SARS-CoV-2 (22). We model this by allowing PCR tests to detect infections starting four days after exposure and up until 11 days after exposure.
If an agent receives a positive test result (after the specified result turnover time of the respective test technology), their category 1 contacts (52) are traced and quarantined. In our simulations, for the calibration, category 1 contacts were those with “close” or “intermediate” links to the infected agents. This reflects the practice of Austrian schools to trace and quarantine these types of contacts in the time period used for calibration. For other simulation runs (i.e., non-calibration), category 1 contacts were defined as only those with “close” links to the infected agent. This reflects the changed practice in Austrian schools after the re-opening of schools in February 2021.
Tracing is considered to occur instantly and contact persons are quarantined without time delay, as soon as a positive test result returns. Quarantined agents will stay in quarantine for 10 days, corresponding to the recommendations of the Austrian authorities regarding the quarantine of contact persons (52). Quarantined agents stay in quarantine, even if they receive a negative test result during that time.
J.4. Contact networks
The contact networks for schools are modeled to reflect typical social interaction structures in Austrian schools (see SI section 1 for details), following interviews with school personnel to gather information on the daily life in Austrian schools during the pandemic (see Section M and SI Section 4). Schools are defined by the number of classes they have and the school type, which determines the age structure of their students. For every school type, we use the average number of classes and the average number of students per class as reported in the most recent Austrian school statistics (30). The number of teachers in a given school is determined based on the number of classes and the school type, given the number of teachers per class listed in the Austrian school statistics (30). Adjustments for daycare and extra language teachers in certain school types were made as they were pointed out to us in the stakeholder interviews (see also SI Section 1). The Austrian school statistics do not differentiate between schools with and without daycare. Therefore we assume that schools with and without daycare are not significantly different in the number of classes and the number of students per class. Nevertheless, the number of teachers in schools with daycare is slightly higher in primary and lower secondary schools. See Table 2 for the number of classes, students and teachers for every school type modelled in this work. Every student and teacher has a number of family members drawn from distributions of household sizes and a number of children corresponding to Austrian households (53). For students we additionally impose the condition on the distributions that each household has at least one child. If a student household has a second child (sibling) that is eligible (by age) to attend the same school, the sibling will also be assigned to an appropriate class in the school, if there is still room. This practice reflects the distribution practice of children to schools in Austria, were efforts are undertaken to enable siblings to attend the same school. Students, teachers and household members are nodes in the contact network. Two exemplary contact networks are shown in Figure 2.
Number of classes, students and teachers of typical schools of different school types in Austria. The number of teachers was determined based on the allocation formula per school type as well as interviews with teachers and principals.
Contacts (edges) between different agents in the contact network are derived from a variety of situations that create contacts between the involved agents in the school context. In addition, every contact is qualified by a contact strength that can be “close”, “intermediate” or “loose”. The possible contact types for different situations, the participating agent groups and the respective contact strengths are listed in Table 3.
Contacts that arise from different situations in the school context between different agent groups. Contacts are always bi-directional. Every contact is qualified by a contact strength (close, intermediate, loose), that condenses both the typical duration and physical proximity of participating parties.
All contacts that occur in households are considered “close”, reflecting the long hours and closeness that characterize contacts between household members. For students in the same class, we assume that all students have contacts of strength “loose” to all other students in the same class, reflecting aerosols that spread in the classroom and are inhaled by the students. Table neighbours are assumed to have contacts of strength “intermediate”, mirroring conversations between students that are physically close to each other, and a higher viral load through aerosols that are exhaled in close physical proximity. In addition to contacts during lessons, students also have contacts of strength “loose” to other students that are in the same daycare group for school types that offer day-care. This is an important factor since in practice (according to the stakeholder interviews), daycare groups are not composed of students from the same class but rather consist of an independent distribution of students to groups and therefore result in the mixing of students between classes. Mixing between classes is also caused by siblings, that attend different classes but have a (household) contact of strength “close”. We do not include other contacts between students of different classes (for example during lunch breaks or in hallways), since all schools we interviewed told us that they go to great lengths to prevent these contacts through a variety of measures. We also do not include social contacts between students of different classes, since schools informed us that most students have the vast majority of friends in the same class.
Teachers can have a variety of contacts with each other. Teachers regularly engage in conversations with colleagues at the workplace and often are close friends with some of their colleagues. Literature on these social networks among teachers is scarce but there is a study (54) that puts the network density score to “engage in conversation regularly” between teachers at 0.25 and to “socialize with outside school” at 0.06, which is consistent with the evidence gathered during the stakeholder interviews. To model these contacts, we randomly create a number of connections of strength “intermediate” (socialize) and “loose” (conversation) between teachers that reflects these network density scores. In addition, team teaching as well as joint supervision of daycare groups creates contacts between teachers that teach the same class at the same time or supervise the same daycare group. These contacts both are of strength “intermediate”, since in these situations teachers spend an extended period of time together, often while talking.
Lastly, teachers have contacts to students in the classes they teach and in the daycare supervision groups they supervise. We qualify these contacts as “intermediate”, since the situations they characterize are usually long (one lesson lasts for 45-60 minutes, daycare supervision lasts between 2 and 4 hours). Nevertheless, one could argue that these contacts should be only of strength “intermediate” if the transmission occurs from a teacher to a student and “loose” if transmissions from students to teachers are considered, since in these situations teachers do a much larger share of the talking than students and will produce more aerosols. We chose to disregard this additional complexity and recognize it as a limitation of our study.
Contacts in our contact network are dynamic and do not exist on every day of the week, reflecting the periodic organization of teaching in Austria. Students are usually at school from Mondays through Fridays and are at home on Saturdays and Sundays. To reflect this, on weekends only household contacts exist between agents. To implement the prevention measure of reduced class sizes, we remove all school-related contacts for a fraction of the students of every class on every second day.
K. Calibration and parameter choices
Some model parameters can be taken over from the existing literature (see Section J.2) or empirical observations of characteristics of infection spread in the school context in Austria (see Section I). For our model, that leaves a total of four free parameters that have to be calibrated to reproduce the observed dynamics of infection spread as closely as possible: (i) the base transmission risk of a household contact (“close”), β, (ii) the weight of contacts of strength “intermediate” as compared to a “close” contact, c1, (iii) the weight of contacts of strength “loose” as compared to a “close” contact, c2, and (iv) the linear age dependence of transmission risk and susceptibility, which we consider to have the same slope c3 and an intercept of 1 for agents aged 18 or older.
K.1. Household contacts
The cumulative risk of adult members of the same household to get infected over the course of the infection of an infected household member is currently estimated as 37.8% (55). We calibrate the base transmission risk, β, between adult agents in our model such that it reflects this cumulative transmission risk. For household transmissions between adults, the only relevant factors that modify the base transmission risk are the reduction due to the progression of the disease, q4(t), and the reduction in case of an asymptomatic course, q5. The values for both of these factors are taken from the literature (40, 42, 46). Therefore, for one contact on day t after the exposure, the probability of a successful transmission is given as
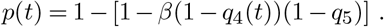 In our model, we draw the relevant epidemiological parameters (exposure duration, infection duration, symptomatic course) from corresponding distributions (37–43) individually for every agent. To calibrate β, we create pairs of agents and let one of them be infected. We then simulate the whole course of the infection (from day 0 to the end of the infection duration n) and perform a Bernoulli trial for the infection with a probability of success p(t) on every day t. We minimize the difference between the expected number of successful infections (37.8%) and the simulated number of successful infections by varying β. This results in an optimal value of β = 0.074 or an average risk of 7.4% per day for a household member to become infected. We note that the reduction of transmission risk and susceptibility due to the age of the transmitting and receiving agents is treated and calibrated separately. This is why we only calibrate the transmission risk between adults here and calibrate the age discount factor for transmission and susceptibility separately.
In our model, we draw the relevant epidemiological parameters (exposure duration, infection duration, symptomatic course) from corresponding distributions (37–43) individually for every agent. To calibrate β, we create pairs of agents and let one of them be infected. We then simulate the whole course of the infection (from day 0 to the end of the infection duration n) and perform a Bernoulli trial for the infection with a probability of success p(t) on every day t. We minimize the difference between the expected number of successful infections (37.8%) and the simulated number of successful infections by varying β. This results in an optimal value of β = 0.074 or an average risk of 7.4% per day for a household member to become infected. We note that the reduction of transmission risk and susceptibility due to the age of the transmitting and receiving agents is treated and calibrated separately. This is why we only calibrate the transmission risk between adults here and calibrate the age discount factor for transmission and susceptibility separately.
K.2. Cluster sizes and group distributions
For the calibration of the other three free parameters, we compare the distribution of cluster sizes and the distribution of the number of infected agents across the agent groups “student” and “teacher” between our simulation and empirically observed clusters in Austrian schools (see Section I).
During calibration, for the other simulation parameters we use settings that most closely match the situation in Austrian schools in the time period from which the empirical observations were taken (weeks 35-46, 2020). Source cases are drawn from the empirically observed distribution of source cases between teachers and students (see Figure 1 A). The age dependence of the probability of developing a symptomatic course of infection is matched to the empirically observed age-dependence (see Figure 8). Only diagnostic testing with PCR tests with a one-day turnover was in place, followed by a background screen in case of a positive result. There were no preventive screens and no follow-up tests after a background screen. Contacts of type “close” and “intermediate” were considered to be “category 1” contacts (52) and were quarantined for 10 days and remained isolated for the full quarantine duration, even in case of a negative test result during isolation. Teachers and students did not regularly wear masks during lessons. Teachers and students did wear masks in hallways and shared community areas and contacts between students of different classes were avoided. All students of a class were present every day i.e., no reduction of class sizes was employed.
Ratio of asymptomatic cases by age group. Age groups 6-10 years, 11-14 years and 15-18 years correspond to the usual age of students in primary, lower secondary, and upper secondary schools in Austria.
For the calibration, we match the cluster characteristics of our simulations with the cluster characteristics of empirically observed clusters in Austrian schools. Specifically, we optimize the sum of the χ2-distance between the empirically observed cluster size distributions and the cluster size distributions from simulations e1, and the χ2-distance between the distribution of infected to the agent groups teacher and student e2. Using the settings for prevention measures described above, to find optimal values for the free parameters, we first conduct a random search in the parameter grid spanned by the following ranges ([start:stop:step]): c1: [0:1:0.05] (intermediate contact weight), c2: [0:1:0.05] (loose contact weight), and c3: [0.0:0.1:0.02] (transmission risk age dependency), where we impose the additional constraint on parameter combinations that c1 > c2. We randomly chose 100 parameter combinations (c1, c2, c3) out of the 950 possible ones and simulate ensembles of 500 runs for each parameter combination and school type. Since the empirical data we compare our simulation results to does not differentiate between schools with and without daycare of a given school type, we assume that 50% of the schools of a given school type are schools with daycare. This approximates the percentage of schools with daycare in Austria (56). We therefore simulate ensembles for primary schools, primary schools with day-care, lower secondary schools, lower secondary schools with daycare, upper secondary schools (no daycare in this school type), secondary schools and secondary schools with day-care. We calculate the overall difference between the simulated and empirically observed cluster characteristics as
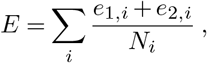 where Ni is the number of empirically observed clusters for school type i. After we identify the parameter combination that minimizes E in the random grid search, we perform a refined grid search around the current optimal parameter combination and repeat the optimization process as described above. We find that a parameter combination of c1 = 0.85, c2 = 0.75, c3 = 0.02 produces cluster characteristics that most closely match the empirically observed clusters. This means that contacts of strength “intermediate” have a transmission risk that is reduced by 15% as compared to household contacts and contacts of type “loose” have a transmission risk that is reduced by 25% as compared to house-hold contacts. Children that are younger than 18 years have a transmission risk that is reduced by 0.02(18 − y)%, where y is the age. We use this optimal parameter combination for all subsequent simulations to analyze the effect of different prevention strategies on cluster characteristics in schools.
where Ni is the number of empirically observed clusters for school type i. After we identify the parameter combination that minimizes E in the random grid search, we perform a refined grid search around the current optimal parameter combination and repeat the optimization process as described above. We find that a parameter combination of c1 = 0.85, c2 = 0.75, c3 = 0.02 produces cluster characteristics that most closely match the empirically observed clusters. This means that contacts of strength “intermediate” have a transmission risk that is reduced by 15% as compared to household contacts and contacts of type “loose” have a transmission risk that is reduced by 25% as compared to house-hold contacts. Children that are younger than 18 years have a transmission risk that is reduced by 0.02(18 − y)%, where y is the age. We use this optimal parameter combination for all subsequent simulations to analyze the effect of different prevention strategies on cluster characteristics in schools.
K.3. Ventilation
Using the COVID-19 transmission risk calculator (33, 57), we calculate the ventilation efficiency of a short and intensive ventilation of the classroom once per hour during one lesson for the teacher and student source case. According to the building regulation for schools in Austria (58), classrooms must have a minimum area of 1.6 m2 / student and a total minimum area of 502 in primary and lower secondary schools. Since the maximum class size we simulate (secondary schools) is 30 students (30*1.6 m2 = 48m2), we can assume all classrooms have a size of approximately 50 m2. The individual infection risk is independent of the number of people in the room. Mask wearing linearly reduces infection risk and is therefore modelled as a separate parameter that influences the infection risk.
To calculate the reduction of transmission risk for one ventilation / hour, we therefore use the following parameters for the teacher source case:
Speaking volume: 3 (loud talking is assumed during teaching)
Mask filter efficiency (exhale): 0
Mask filter efficiency (inhale): 0
Ratio of time speaking: 50% (teacher teaching a class)
Breathing volume [l/min]: 10 (adult)
Room area 50 m2 (building regulations (58))
Room height 3.2 m (building regulations (58))
Duration: 1 hour (one lesson)
Air exchange rate: 2 (corresponding to one ventilation / hour)
This results in an an individual infection risk of 1.9% per person in the room. Compared to the individual infection risk if of 5.3% for no room ventilation (air exchange rate of 0), this is a reduction of 64%.
For the student source case, we use very similar parameters, except for the speaking volume (2, normal talking), the ratio of time speaking (10%) and the breathing volume (7.5 l/min, child). This results in an individual infection risk of 0.2% if the room is ventilated once per hour and 0.55% for no ventilation. Therefore ventilation also reduced the infection risk by 64%.
L. Calculating the reproduction number
R. We use the reproduction number calculated from infection chains in our model to report and compare outcomes of different intervention scenarios. Since our model is agent-based, R is calculated as an individual-level measure (59) by counting the number of secondary infections a focal individual has caused. Since the number of agents in our model is rather small (𝒪 (103)), we expect the finite size of the model to significantly influence the number of secondary infections as the infection spreads through the system, since the pool of susceptible agents is not infinite and depletes with time. To minimize this effect, we calculate the reproduction number, R, of an ensemble of simulations as the average number of secondary infections caused by the source case only, disregarding the rest of the transmission chain. This approach is warranted since source cases are picked at random and no systematic biases are introduced by the local connectivity of the contact network of the source case.
While in this case R is not a model control parameter that determines whether the number of infected will grow or decline, as in the classical SIR model, it is still a useful indicator to assess how likely a wide spread of the infection through the system is. If R < 1, for the majority of cases the source case will only infect one or no other agents. This does not exclude the possibility for rare larger clusters, but they are much less likely as for settings for which R > 1.
M. Interviews with school personnel
We conducted semi-structured interviews with a total of eight teachers and principals of Austrian schools (1 primary, 3 lower secondary, 1 upper secondary, and 3 secondary). The aim of the interviews was to get an impression of daily life in Austrian schools during the pandemic. The gathered information was used in three ways: (i) to design the school type specific contact networks, (ii) to design the intervention measures and (iii) to assess potential problems with the implementation of intervention measures. Interviews were conducted over video chat. The questionnaire used to guide the interviews is provided in SI Section 4.
N. Online visualization
The online visualization aims to convey our simulation results to decision makers, as well as more general audiences, such as students and parents. Since we cannot assume our audience to be familiar with statistics or simulation, we designed our visualization in a way that allows us to guide a user through the supplied information in four sequential sections (I-IV). (I) We first provide a graphical overview of our simulation results for different measures and school types, similar to the one in Figure 4. We then provide general information on calibration data that could be of interest to the general public, such as the infectiousness of a person during the course of their infection. (II) Users who want to explore further can then investigate detailed results for a specific school by using an input mask to configure school type and size (number of classes, and class size). The number of teachers is automatically derived from the school type and size. (III) Once a school is configured, the user is supplied with two histograms detailing the cluster size and number of quarantine days for all combinations of measures (see Figure 9). The plots are interactive and can be re-sorted by measure in order to enable a better comparison of the individual measure effects. By default, we display the 0.9 percentile outcome of our simulations (“worst case”). Users also have the option to investigate the median and 0.1 percentile scenarios. If a user wants to see how an infection in a specific scenario (set of measures) plays out, they can select the respective histogram bar in order to switch to the cluster simulation view. (IV) The cluster simulation (see Figure 10) shows an animation of the simulated events that led to the results of the selected set of measures for the specified school. The animation illustrates the daily school routine of students and teachers (depicted as circles) within a schematic school floor-plan. The shape of a circle indicates the agent type (student or teacher). The color indicates the state of an agent (susceptible, exposed, infected, recovered). All sections of our visualization are accompanied by explanatory texts, in order to ensure users are informed about the functionality and the displayed information in each section. Users can switch between sections via the navigation menu on the top of the web page, and also share the results of their exploration by generating a URL that stores their school and measure selections.
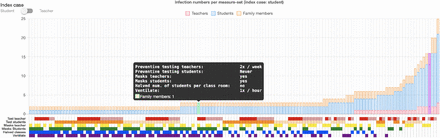
Overview of the online interactive simulation viewer displaying the effects of measure combinations on cluster size. Each bar represents one set of measures. Bars are separated into three stacks, representing the number of infected students, teachers, and family members. The bar representing the currently selected set of measures is highlighted in purple (right). A popup window displays the measure configuration of a bar on mouse-over. Below the chart, six rows of colored squares visually encode the set of measures that yielded the respective simulation result. A row (representing a measure) can be clicked, in order to re-sort the plot by the selected measure and thus enable a better comparison of the measure’s effects. The button on the top left corner allows a user to switch the results shown in the plot between simulations that had a student or a teacher as a source case.
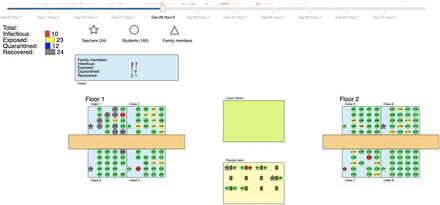
The “outbreak simulation view” in the online visualization displays the schedule of students and teachers over time, illustrated in a schematic view of the respective school. Agents (nodes) change their color according to their current infection state: susceptible (green), exposed (yellow), infectious (red), recovered (grey). Red bars on the timeline (top) indicate when infections occur. Outside of school-hours, agents spend their time at home (indicated by a single box on the top left) where infections with family members can occur. Family members are hidden from the animation, but their state is tracked as well, and displayed as a histogram on top of the home. A summary of the state of all agents is displayed on the top left corner below the time line.
Data Availability
The code for the agent based simulation model is openly available under an MIT license. Cluster data used to calibrate the model is available upon request.
Code availability
The code for the agent based simulation model is openly available (36) under an MIT license.
Data availability
Cluster data used to calibrate the model is available upon request.
Acknowledgments
JS and ST acknowledge financial support from the Austrian Science Promotion Agency FFG under 882184 and JL and PK from the Vienna Science and Technology Fund WWTF under MA16-045. PK and ST are grateful for support from the Medizinisch-Wissenschaftlichen Fonds des Bürgermeisters der Bundeshauptstadt Wien, no. CoVid004. We are greatly indebted to the Carinthian Department of Education and to numerous principals and teachers supporting this work. We thank Wolfgang Knecht for help with the visualization. The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC).