Abstract
Background Around 40% of school leavers in the UK attend university and individual universities generally host thousands of students each academic year. Bringing together these student communities during the COVID-19 pandemic may require strong interventions to control transmission. Prior modelling analysis of SARS-CoV-2 transmission within universities that use compartmental modelling approaches suggest that outbreaks are almost inevitable.
Methods We constructed a network-based model to capture the interactions of a student population in different settings (housing, social and study). For a single academic term of a representative campus-based university, we ran a susceptible-latent-infectious-recovered type epidemic process, parameterised according to available estimates for SARS-CoV-2. We investigated the impact of: adherence to (or effectiveness of) isolation and test and trace measures; single-room isolation of cases; supplementary mass testing.
Results Incorporating uncertainty in the asymptomatic fraction of cases and their associated infectivity, in the absence of interventions our model estimated that 69% (55% - 75%) of the student population could be infected during the autumn term. With full adherence to test, trace and isolate measures, we found lower cumulative infection estimates of 19% (5% - 39%). Irrespective of the adherence to isolation measures, on average a higher proportion of students resident on-campus became infected than off-campus. Room isolation generated minimal benefits. A one-off instance of mass testing would not drastically reduce the term-long case load, though if performed a couple of weeks before the end-of-term it could reduce the expected end-of-term prevalence. Regular testing, together with high adherence to isolation, test and trace measures, could reduce the proportion infected during the term by more than 50% compared to having no mass testing.
Conclusions Our findings suggest SARS-CoV-2 may readily transmit in a university setting if there is limited adherence to nonpharmaceutical interventions and/or there are delays in receiving test results. Following isolation guidance and effective contact tracing curbed transmission and reduced the expected time an adhering student would spend in isolation. Additionally, widespread adherence throughout the term suppresses the amount of unwitting asymptomatic transmission to family and community members in the students’ domicile regions after term ends.
Introduction
Globally, many countries have employed social distancing measures and nonpharmaceutical interventions (NPIs) to curb the spread of SARS-CoV-2 [1]. In the UK, the enaction of lockdown on 23rd March 2020 saw the closure of workplaces, pubs and restaurants, and the restriction of a range of leisure activities. The education sector was also impacted, with schools closed (with the exception of children of key workers) and higher education establishments, such as universities, delivering the end of the 2019/2020 academic year via online means.
In the summer months, the national implementation of strict measures transitioned to a localised approach, targeting regions experiencing the highest burden of transmission. As the number of SARS-CoV-2 confirmed hospitalised cases and deaths began to decline, many sectors of society cautiously reopened, with measures in place to reduce transmission. Universities began to develop plans to reopen, with several adopting a blended learning strategy of limited face-to-face teaching combined with online lectures. Higher education in the UK comprises a sizeable population of students, with over 2.3 million higher education students enrolled in the 2018/2019 academic year across over 160 higher education providers [2]. This results in a sizeable movement of students nationwide at the beginning and end of academic terms (in addition to international student travel). The migration of students would contribute to increased population mobility, which had already grown since the easement of lockdown measures occurred [3, 4], with an associated need for careful management in order to minimise the risk of seeding outbreaks in low prevalence locations.
As of 7th November 2020, the United Kingdom (UK) has reported in excess of one million cases and more than 48,000 COVID-19 deaths [5]. There is, however, a lower risk of severe case outcomes in typical student age groups compared with older sections of the population; a higher proportion of cases are expected to be asymptomatic [6], while hospitalisation and mortality rates are lower [7]. In particular, of 34, 374 COVID-19 associated deaths in hospitals reported in England by 6th November 2020, 235 (0.007%) were 20-39 years of age [8].
Nevertheless, the typical contact patterns of students means they could have significant potential of transmitting the virus within their social group, amplifying the risk of infection to staff members and those in the local community who may be more vulnerable. Contact studies indicate that students, and in general those aged 20 to 30, report higher numbers of social contacts in their everyday lives compared with other age-groups and occupations [9]. In addition, as a consequence of those of younger age being more likely to experience asymptomatic infection, there is the prospect of infected students returning home at the end of term in an asymptomatic state, heightening the risk of unwittingly transmitting to more vulnerable family members.
A small number of modelling analyses have already been carried out pertaining to transmission of SARS-CoV-2 within universities, and subsequent levels of COVID-19 disease [10]. These modelling studies have been predominately US-focused [11–15], potentially due to their earlier return. Paltiel et al. [11] modelled the effect of a variety of testing strategies on the number of infections that would arise among 5,000 students during an 80-day semester. Cashore et al. [12] and Lopman et al. [14] investigated the impact of testing, screening and isolation for Cornell’s Ithaca campus and Emory University in Atlanta, Georgia, respectively.
With regard to UK Higher Education institutions, the size and set-up of universities can differ markedly to US counterparts, influencing contact patterns and thus the spread of infection. Though the majority of prior work has not had access to realistic contact structures within the university setting, Brooks-Pollock et al. [16] have developed a stochastic transmission model based on realistic mixing patterns between students and applied to the University of Bristol. Other UK-centric work has included investigations into the expected number of cases that may be present at the outset of the autumn term in 2020 [17], and a working paper looking at how mathematical approaches may help inform the reopening of higher education spaces to students whilst minimising risk [18].
Many of the previous studies of SARS-CoV-2 outbreaks in a university setting have adopted compartmental modelling approaches, in which individual behaviour and interventions such as contact tracing cannot be readily captured. In this paper, we present an individual-level network-based model framework for transmission of SARS-CoV-2 amongst a student university population, which includes test, trace and isolation interventions. Contacts occur across household, study and social settings, underpinned by empirical data where possible. We find that maintaining strong adherence to isolation guidance and engagement in test and trace could both curb the amount of infection throughout the academic term and limit SARS-CoV-2 prevalence at the beginning of the winter break. Use of room isolation and a single mass testing instance may offer marginal benefits, though the underlying adherence to interventions remains crucial. These results show the possible impact of SARS-CoV-2 transmission intervention measures that may be enacted within a university population during the forthcoming academic year.
Methods
To enable a modelling analysis of the transmission of SARS-CoV-2 within a university population, we adopted a network approach to capture the interactions between students in different settings, upon which we ran an epidemic process. In this section we provide in some detail: (i) a description of the network model; (ii) the data sources used to parameterise the network contact structure; (iii) the model for SARS-CoV-2 transmission and COVID-19 disease progression; (iv) the simulation protocol employed to assess the scenarios of interest.
Network model description
We used a multi-layered network model to encapsulate identifiable groupings of contacts. Our model was comprised of four layers: (i) households, (ii) study groups/cohorts, (iii) organised societies and sports clubs, and (iv) dynamic social contacts.
Household contact layer
In our model we considered contact networks on campus and off campus separately. The network for on-campus accommodation contained a hierarchical structure, from the smallest scale to largest, of a household (typically based around a shared kitchen), floor, block, hall (comprised of multiple blocks). We constructed the on-campus accommodation units to match that of a representative campus based university. We assigned students resident off-campus to households with sizes sampled from an estimated student household size distribution (see Supporting Text S1: Off-campus student household size).
Within a household, irrespective of on-campus or off-campus location, we assumed each individual to have the potential to transmit infection to each other person within their household (i.e. a fully connected network). In addition, on any given day, on-campus students could randomly make contact with any other individual outside their direct household, though situated on the same floor or contained within the same accommodation block.
Study/cohort contact layer
We partitioned the student population into 84 cohorts based on department and stage of study: first year undergraduate, non-first year undergraduate, postgraduate (see Supporting Text S2: Cohort data). To generate the contacts made within each cohort, we used a configuration model [19] to allow the specification of a desired degree distribution.
Note that we assumed these cohort contacts occurred between study friendship groups outside of any face-to-face classes. In other words, we have presumed for teaching spaces the enforcement of COVID-secure measures sufficiently minimises the transmission risk to prevent the onward spread of infection within that setting.
Contacts in organised societies and sports clubs
A prominent aspect of the university experience is the presence of societies and sports clubs. For constructing contacts resulting from involvement in such groups, we applied a uniform probability of forming a contact with each other individual in the group, with that probability differing based on whether the group was a society or sports club. As simplifying assumptions, these links did not alter during the course of a simulation and we set each social group to meet three times per week with assigned members attending all sessions.
Dynamic social contacts
The final contact layer sought to capture random, dynamic, contacts made each day with any other individual in the student population. For each timestep, random connections were selected for each student according to a specified cohort-dependent distribution. We carried out the contact network generation using the ErdÖs-Rényi model [20], which assumes a Poisson distribution degree sequence.
Contact parameterisation
We characterised the network structure across the various contact layers by applying two differing approaches.
The first method was a data-driven approach, using data from the Social Contact Survey [9, 21]. The Social Contact Survey was a paper-based and online survey of 5,388 participants in the United Kingdom conducted in 2010. We extracted records provided by 347 students, with a total of 10,302 contacts. These data informed the network construction parameters for the cohort and dynamic social contact layers, with stratification according to the student’s level of study (undergraduate or postgraduate). We fit parameters for these contact distributions using maximum likelihood estimation via the fitdistrplus package in R.
The second method was a subjective approach, used when we did not have relevant empirical measures available to enable the parameterisation of the given contact layer. This was applied to the formulation of random contacts within on-campus accommodation blocks (though outside the direct household) and organised social club contacts. We provide a summary of the network parameterisation in Table 1.
Description of network contact parameters.
Cohort contacts
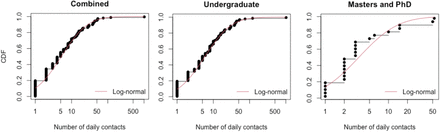
To estimate the number of contacts occurring with those in the same study cohort, we used the student contact survey records listed as occurring in the work or school setting. We kept entries specifying a duration of 60 minutes or more and that occurred more than once per week, assuming the retained contacts with these characteristics would be reflective of a university study cohort. We independently fit using maximum likelihood estimation lognormal distributions for undergraduates and postgraduates, using a mean and standard deviation parameterisation, acquiring distributions of Lognormal(1.646,1.590) and Lognormal(1.211,1.128), respectively (Fig. 1).
Black dots and lines depict the empirical data. The red solid line corresponds to the best-fit lognormal distribution.
Dynamic social contacts
For estimating a distribution for dynamic social contacts, we considered contacts reported within the Social Contact Survey occurring in all locations except home and all non-’first-time’ contacts. We limited valid contacts to those recorded as either involving touch or lasting longer than 10 minutes. Valid contacts also had to last less than 60 minutes, with a view that longer duration contacts would be captured by the cohort and society contact layers.
Overall, undergraduates and postgraduates had a very similar number of social contacts (daily medians of 5.19 and 4.9 respectively). We acquired lognormal distributions with mean 1.748, standard deviation 1.331 for undergraduates, and mean 1.223, standard deviation 1.125 for postgraduates (Fig. 2).
Black dots and lines depict the empirical data. The red solid line corresponds to the best-fit lognormal distribution.
Random on-campus accommodation contacts
Given the limited available data to be able to parameterise a degree distribution for those contacts, we took a pragmatic approach and assumed a low constant probability of contacts occurring in the broader accommodation unit. We additionally assumed these contact probabilities lessened for higher levels of accommodation hierarchy. Specifically, we attributed a higher chance of interacting with someone on the same floor (daily chance of contact of 10%) than someone on another floor within the same block (daily chance of contact of 5%). We assumed no random accommodation associated contacts with other students living in different blocks in the same hall.
Contacts in organised society and sports club activities
We also did not have available the necessary information to parameterise contacts within organised social groups using a data-driven approach. Therefore, we stress that the values stated here are subjective and alternative proposals would add to result variability.
We considered a community of 335 organised social groups, comprising 270 societies and 65 sports clubs. In the absence of a membership size distribution, we allowed a breadth of group sizes by randomly assigning each group a membership size of 10 to 100 (in increments of 10). We also subjectively chose a monotonically decreasing probability mass function for the number of organised social groups students actively participated in: 50% of students not in any group; 40% involved in a single group; 2.5% a piece in two, three, four or five groups.
Following group assignment, within each group we established contacts between students with a fixed probability of each link existing. These probabilities we set at 0.05 for societies and 0.1 for sports clubs. Accordingly, a student was likely to make more contacts in groups with large membership. For simplicity, we retained the same arrangement of contacts for each meeting.
Epidemiological model
Disease states
We ran a susceptible-latent-infectious-recovered (SEIR) type disease process on the network structure. Once infected, we assumed infectiousness could not start immediately (i.e. on the same day), with the earliest permitted moment being the following day. We assumed an Erlang-distributed incubation period, with shape parameter 6 and scale parameter 0.88 [22].
The distribution of infectiousness had a four day pre-symptomatic phase, followed by a seven day symptomatic phase. This gave a total of 11 days of infectivity and a minimum 12 day infection duration (for the full temporal profile, see Table 2). It was based on a Gamma(97.2,0.2689) distribution, with shape and scale parameterisation, shifted by 25.6 days [23, 24]. Following completion of the infectious period, the individual entered the recovered state.
Description of epidemiological parameters.
Asymptomatic transmission
Infected individuals could be either asymptomatic or symptomatic, with an ascribed probability determining the chance of each individual being asymptomatic. There remains uncertainty in the fraction of COVID-19 cases that are asymptomatic and how that statistic may vary with age, however community surveillance studies have been performed to help diminish this uncertainty. The REal-time Assessment of Community Transmission-1 (REACT-1) study found approximately 70% of swab-positive adults and 80% of swab-positive children were asymptomatic at the time of swab and in the week prior [25]. To reflect the uncertainty in this value, which includes a portion of the previously stated estimate being presymptomatic infected individuals who would later go on to display symptoms, and the proportion of people who tested positive and were non-symptomatic being lower in round 5 at 50% [26], in each simulation we sampled the asymptomatic case probability from a uniform distribution within the interval 0.5 and 0.8.
There is currently limited data available to provide a robust quantitative estimate of the relative infectiousness of asymptomatic and symptomatic individuals infected with SARS-CoV-2, though there are some indications that asymptomatic individuals could be considered to be less infectious than symptomatic individuals [27, 28]. Therefore, we set an asymptomatic individual to have a lower risk of transmitting infection compared to a symptomatic individual, with the current uncertainty reflected by sampling the value for the relative infectiousness of an asymptomatic in each simulation replicate from a Uniform(0.3,0.7) distribution. We applied the scaling consistently throughout the duration of infectiousness for asymptomatics, meaning there was no time dependence on the scaling term over the course of infectiousness.
Setting transmission risk
Attributing risk of transmission to any particular contact in a particular setting is complex. This is partly due to the huge heterogeneity in contact types, and partly due to the different scales of data: contact information is by its nature individual-based, whereas transmission rates are generally measured at the population level. Therefore, whilst we can attribute a relative risk to each contact type (home, social, study), there is an arbitrary scaling to translate these relative risks to an absolute growth rate of infection in the population.
For household transmission, we attributed a household secondary attack rate to each individual based on their household size. We sampled from a normal distribution whose mean value depended on the household size, based on estimates of adjusted household secondary attack rates from a UK based surveillance study [29]. The mean values used were: 0.48 for a household size of two, 0.40 for for a household size of three, 0.33 for a household size of four, 0.22 for a household size of five or above. The standard deviation of the normal distribution for households of size two or three was 0.06, and for households of four or above was 0.05.
For transmission risk in other settings, we performed a mapping from the Social Contact Survey [9] to obtain a relative transmission risk compared to the central estimate of adjusted secondary attack rate in the household setting against those aged 18-34 of 0.34 [29] (further details in Supporting Text S3: Parameterisation of contact risk). The relative magnitude of those means when compared to the household transmission risk were used to scale the standard deviation. Transmission risks were consistent across all non-household settings, with the exception being in student societies where we assigned a lower transmission risk to reflect the implementation of COVID-secure measures that would be required to permit these meetings to take place. We also reiterate that we attributed zero transmission risk to face-to-face study.
To calibrate the relative transmission risks to achieve an uncontrolled reproductive number, Rt, in the expected range of 3 − 4, we applied a universal scaling of 0.8 to all of the above rates (see Supporting Text S4: Non-intervention scenario calibration).
Isolation, test and trace
Testing and isolation measures
Upon symptom onset, students adhering to guidance enter isolation for ten days. At that moment, fellow household members of the symptomatic case that adhere to guidance enter self-isolation for 14 days [30]. Students that are symptomatic and that will engage with the test and trace process take a test upon symptom onset. We included a two day delay before receiving the test result.
Once isolation periods are begun they are seen out in full unless the test result was negative (false negative probability of 0.13 [31]). On occasions where a negative result was given, household members would be released from isolation, as long as no other symptomatic cases (that are confirmed positive or awaiting test result) were present in the household. The index case remained in self-isolation if they had independently been identified via contact tracing as a contact of a known infected; otherwise, that student also left self-isolation.
Forward contact tracing
Contacts of a confirmed case, and that were adhering to self-isolation guidance, spent up to 14 days in self-isolation [32]. We set the time required to be spent in self-isolation to elapse 14 days from the day the index case became symptomatic.
The modelled tracing scheme looked up contacts for an index case up to two days before onset of symptoms. We assumed that the probability of an individual being able to recall their ‘dynamic’ contacts diminishes with time, from 0.5 one day previously, reducing in increments of 0.1, such that the probability of successfully tracing a contact five days prior to the tracing occurring is 0.1. Once again, other assumptions could be explored and a wider range of assumptions, collectively, would generate more variation in the results. We give an overview of isolation, test and trace related parameters in Table 3.
Description of isolation, test and trace related parameters.
Simulation outline
We used this model framework to evaluate the transmission dynamics of SARS-CoV-2 amongst a university student population during the autumn term of the 2020/2021 academic year, and the potential impact of both adherence to the guidance and additional interventions.
We ran all simulations with an overall student population of 25,000, with 7,155 students resident on-campus and the remainder off-campus. Simulation time corresponded to 77 days, encompassing the length of welcome week plus the ten week academic autumn term.
We seeded the number of latent, asymptomatic and recovered individuals based on UK regional prevalence estimates for 26th September 2020 and student flow data (we provide further methodological details in Supporting Text S5: Initial seeding of infected and recovered individuals). We assumed there were no symptomatic infected (ill) students present at the beginning of each simulation replicate.
Our assessment comprised of three strands. First, we analysed how the strength of adherence to guidance on isolation and engagement with test and trace affected case burden and accumulated isolation time (total number of student isolation days over the term). Second, we considered adoption of a policy of strict room isolation for on-campus residents displaying COVID-like symptoms. Third, we analysed a collection of scenarios involving mass testing of students to study the impact on overall case load, the expected time spent in isolation per adhering student and the prevalence of infection at the conclusion of the autumn academic term.
We outline each of the three assessments in further detail below. Unless stated otherwise, for each parameter configuration we ran 1,000 simulations, amalgamating 50 batches of 20 replicates; each batch of 20 replicates was obtained using a distinct network realisation. We performed the model simulations in Julia v1.4 - 1.5.
Adherence to isolation, test and trace
We sampled adherence to isolation from zero compliance (value 0) to full compliance (value 1) in increments of 0.1. We assumed an identical adherence to isolation restrictions independent of the cause (presence of symptoms, household member displaying symptoms, identified as a close contact of an infected by contact tracing). Additionally, we assumed those that would engage with isolation measures would also engage with testing and tracing.
Use of room isolation
For those resident in on-campus accommodation and suffering from COVID-like symptoms, another applicable intervention may be to bolster household isolation by mandating quarantine of those individuals in en-suite rooms (with meals and essentials delivered). Those residing in accommodation with communal bathrooms would be re-housed. Those already living in en-suite accommodation would be isolated in their rooms.
We modelled this intervention by assuming those rehoused or put into room isolation had no contacts. We applied these measures on the same timestep the student reported being symptomatic.
Mass testing
We explored altering the timing and frequency mass testing was carried out: a single instance on day 21 (end of week 2 of the academic term); a single instance on day 63 (end of week 8 of the academic term); regular mass testing every two weeks (‘fortnightly’, on day 1, then day 14, day 28,…, day 70); regular mass testing on a weekly basis (on day 1, then day 7, day 14,…, day 70).
Additionally, we varied coverage amongst the eligible student population: all students, on-campus resident students only, off-campus resident students only. We carried out sensitivity to the underlying adherence to isolation measures by performing the analysis for adherence probabilities of 0.2 (low), 0.5 (moderate) and 0.8 (high), respectively.
We did not include with the mass testing procedure students that had previously reported infection and then subsequently received a positive test. We also assumed that all tests were performed on the same day, those latently infected (thus not yet infectious) would always return a negative test result, and contact tracing was performed rapidly such that those contacts who were both traceable and adhered to isolation guidance were isolated from the next timestep.
Results
Trade-offs between case load and isolation
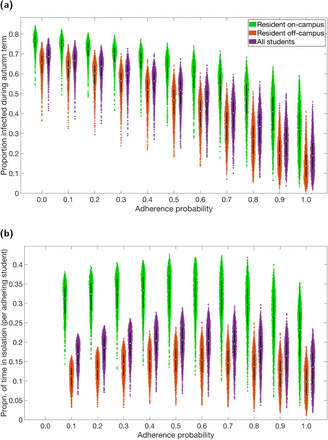
With high adherence to isolation measures and engagement with test and trace, a lower number of infections (the sum of both identified cases and undiagnosed infections) would be expected to arise during the course of the autumn term (Table S3). Specifically, with no interventions we estimated a median proportion of 0.69 (95% prediction interval: 0.55-0.75) of the entire student population to be infected during the autumn term. In contrast, with full adherence the median proportion infected was 0.19 (95% prediction interval: 0.049-0.39). Irrespective of the adherence level, we found that (on average) a higher proportion of students resident on-campus would become infected versus students resident off-campus (Fig. 3(a)).
Outputs summarised from 1,000 simulations (with 20 runs per network, for 50 network realisations) for various levels of adherence to NPIs. Over the duration of the autumn term, distributions relative to students resident on-campus only (green violin plots), students resident off-campus only (orange violin plots) and to the overall student population (purple violin plots) for (a) proportion infected, and (b) proportion of time adhering students spend in isolation. The white markers denote medians and solid black lines span the 25th to 75th percentiles. For percentile summary statistics, see Table S4. Maintenance of nonpharmaceutical interventions and effective contact tracing curbed transmission, with the expected time an adhering student would spend in isolation also reduced. On-campus residents were more likely to become infected and spend a greater proportion of time in isolation compared to students living off-campus.
In addition to strong adherence leading to suppression of case numbers, it also delivered benefits from the perspective of time spent in isolation. Out of those students that would adhere to isolation guidance, those resident on-campus were expected to spend a greater proportion of time in isolation compared to adhering students living off-campus. Further, we witnessed greater variability in the predicted time an adhering individual spent in isolation for those resident on-campus versus those resident off-campus (Fig. 3(b), Table S3).
Inspecting temporal patterns of infection prevalence and proportion of the student community in isolation demonstrated trade-offs between case numbers and the requirement for portions of the population to isolate (Fig. 4). Averaging across all simulation replicates, zero adherence led to the occurrence of a large outbreak that had subsided by the conclusion of the term, although no one entered isolation at any time. With half of the student population adhering to control measures, we observed a slower growth of the epidemic concurrent with a steady rise in the proportion of students entering isolation. Under complete adherence the expected prevalence of infection was kept low, although this generated an initial surge in the amount of students isolating that then stabilised in the latter weeks. With full adherence the number of students expected to be isolated at the end of term was also expected the be greater than if only half of the student community adhered to isolation and tracing guidance.
Outputs produced from 1,000 simulations (with 20 runs per network, for 50 network realisations) for three levels of adherence to nonpharmaceutical interventions: 0% (grey), 50% (blue), 100% (red). Solid lines depict the median profile and shaded regions the 50% prediction interval. Patterns of infection prevalence and proportion of the student community in isolation demonstrated trade-offs between case numbers and the need for portions of the population to isolate. (a) Proportion infected. (b) Proportion isolated.
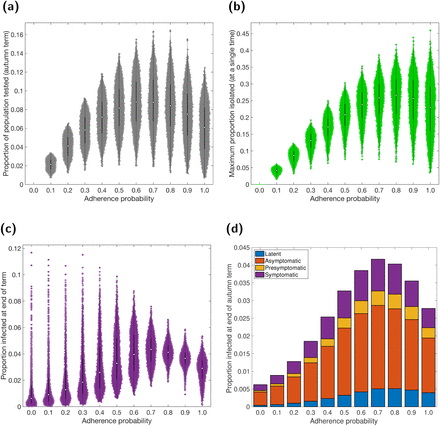
The effect of strong adherence in suppressing case numbers is reflected in the reduction in the amount of tests carried out on those that are infected with SARS-CoV-2, compared to moderate adherence (Fig. 5(a)). For an expected fraction of the population adhering surpassing 0.4, median estimates for the maximum proportion of students isolated at any given time were between 20-30% (Fig. 5(b)). Therefore, for high levels of adherence, the substantial decline in cases compensates for the greater number of individuals who adhere to the rules and isolate as a consequence of the cases identified.
Outputs summarised from 1,000 simulations (on 50 network realisations with 20 runs per network) for various levels of adherence to nonpharmaceutical interventions. White markers denote medians and solid black lines span the 25th to 75th percentiles. (a) Proportion of population infected by SARS-CoV-2 and tested. (b) Maximum proportion of students isolated at any single time. (c) Proportion of students infected at the end of the autumn term. (d) Under each level of adherence, median proportion of student population in latent (blue), asymptomatic (orange), presymptomatic (yellow), symptomatic (purple) infected states at the end of the autumn term. For percentile summary statistics, see Table S4.
Prevalence at the end of term may be as high as 12% of the population under no interventions, whilst for full adherence it is unlikely to be above 5%. The smaller central estimates for low adherences were a consequence of infection having swept through the majority of the student population during the prior weeks (Fig. 5(c), Table S4). Furthermore, in the situation where spread of infection had been subdued during the term due to moderate adherence to NPIs, the results display potential for there being a sizeable number of non-symptomatic infecteds (comprising latent, asymptomatic and presymptomatic) at the end of the term (approximately 3%, Fig. 5(d)). Given complete adherence to NPIs, central estimates for non-symptomatic infecteds at the conclusion of the academic term dropped to roughly 2%, substantially reducing the risk posed by students returning home for the winter break.
Minor gains associated with room isolation as an additional intervention
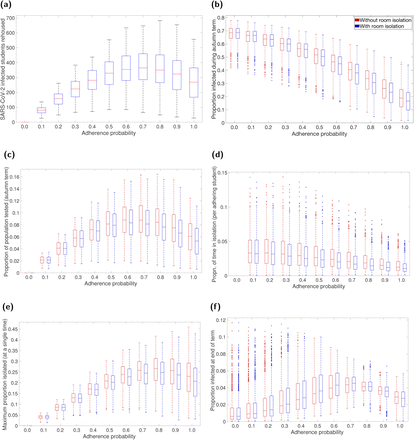
Isolation rooms, where on-campus students reporting symptoms and testing positive are rehoused to prevent further transmission to housemates, has been postulated as an additional measure of social distancing and control. For all tested adherence levels, we found median estimates for the number of on-campus SARS-CoV-2 infected students being rehoused were below 400. In addition, the majority of simulations returned counts less than 600 (Fig. 6(a)). For low adherence, despite the large number of symptomatic cases present in the student population, under-reporting results in fewer rehousing instances compared to situations where there is stronger adherence to NPIs. Similarly to observations for tests used and cumulative isolation time, with high adherence the curbing of spread of infection results in a reduction in the expected number of SARS-CoV-2 infected on-campus students being rehoused.
For specified adherence levels, we compare two scenarios: one without rehousing/room isolation as part of the management strategy (red boxplots), and one including rehousing/room isolation as part of the management strategy (blue boxplots). We ran 1,000 replicates for each scenario. (a) Maximum number of students rehoused at any one time for the additional isolation strategy. (b) Proportion infected. (c) Proportion of population infected by SARS-CoV-2 and tested. (d) Proportion of time adhering students spend in isolation. (e) Maximum proportion of students isolated at any single time. (f) Proportion of students infected at the end of the autumn term. For percentile summary statistics, see Table S4. The addition of a rehousing/room isolation control measure generally resulted in slight reductions in central estimates and a narrowing of distributional ranges across all measures.
When including room isolation as an extra intervention measure, in addition to social distancing, isolation guidance and contact tracing, we observe a slight reduction in the median for estimated case load over the autumn term (Fig. 6(b)). There was also a reduced probability of a large number of cases over the course of the autumn term. The number of tests administered on COVID-19 infected individuals was generally lower (Fig. 6(c)).
When considering the maximum number of students isolated at a single time and cumulative isolation days, central estimates and variability were also reduced when mandating room isolation for students experiencing COVID-like symptoms who were resident on-campus (Figs. 6(d) and 6(e)).
Identifying a preferred mass testing strategy dictated by the objective
Our investigation of the utility of mass testing during the course of the academic term involved three variables: (i) the timing and frequency of mass testing that was carried out: a single instance on day 21 (end of week 2 of the academic term); a single instance on day 63 (end of week 8 of the academic term); regular mass testing on a fortnightly basis (on day 1, then day 14, day 28,…, day 70); or regular mass testing on a weekly basis (on day 1, then day 7, day 14,…, day 70); (ii) the coverage amongst the eligible student population: all students; on-campus resident students only; or off-campus resident students only; (iii) underlying adherence to isolation and contact tracing (tested values of 0.2 (low) 0.5 (moderate) and 0.8 (high), respectively).
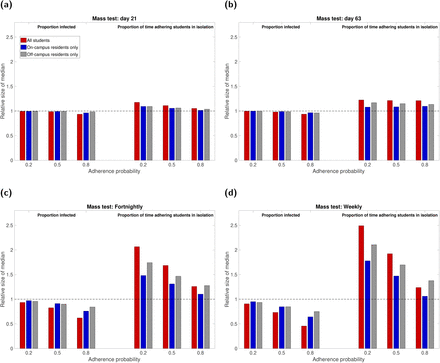
We compared the considered mass testing options to a baseline scenario that had identical parameters with the exception of no mass testing being performed. More intense testing (greater coverage) and earlier testing on average led to a smaller outbreak. However, intense testing resulted in a greater amount of time spent in isolation for those students adhering to isolation measures (Fig. 7). These relationships remain contingent on the proportion of students arriving infected.
Mass testing was either not used (baseline scenario), a single instance took place at the end of week two or week eight of the academic term (corresponding to simulation day numbers 21 and 63, respectively), or regular mass testing was performed on a fortnightly or weekly basis. We present in each panel outputs from 1000 simulations for mass testing covering all eligible students (red), on-campus only (blue), off-campus only (grey). The left hand side of each panel corresponds to the relative proportion (compared to the baseline scenario) of the student population infected over the duration of the autumn academic term under low, moderate and high adherence. In a similar way, the right hand side of each panel presents data on the relative time adhering students spend in isolation. The one-off mass testing was performed on: (a) day 21; (b) day 63. Frequent mass testing was performed (c) fortnightly; (d) weekly. Full estimates are given in Table S5.
In more detail, for the single instance mass testing options and for the high adherence setting, an early mass test (day 21) covering all students resulted in the lowest relative median estimate (0.94) for the proportion infected and caused only a minor increase in the time each adhering student would be estimated to be isolated (1.05, see Fig. 7(a) and Table S5). In contrast, a late date mass test (day 63) of all students, combined with a low adherence to isolation measures, led to a similar minor drop in the proportion infected but a greater increase in the time spent in isolation for those students that do adhere to isolation measures (1.21, see Fig. 7(b) and Table S5).
Given low adherence circumstances, regular testing (either weekly or fortnightly) amplified the characteristic that adhering students are likely to be in isolation for a greater portion of term-time (Figs. 7(c) and 7(d), Table S5). In particular, having weekly mass testing compared to no mass testing led to a doubling in the expected median time that adhering students spent in isolation (in the case of all students being mass tested each round). In a similar manner to the one-off mass test strategies, we found testing that covered all students (combined with high adherence to other control measures) returned the lowest relative median estimate (0.62 and 0.46 for fortnightly and weekly testing, respectively) in the proportion of the student population infected over the course of the academic term. Targeting testing at students resident off-campus only was comparably less effective (proportional size of median estimates across adherence settings ranged from 0.75-0.96).
Across the mass test scenarios there was a large amount of variability in the proportion of infected students at the end of term (Figs. 8(a) to 8(c), Table S6). With the exception of the early single instance mass test strategy, we saw the greatest reductions in median outcomes when mass testing rounds covered all students and adherence to other intervention measures was high (Figs. 8(d) to 8(f), Table S7). The top-performing strategy of weekly mass testing involving all students and high adherence to other control measures resulted in an end of term prevalence roughly two-thirds of the size of the estimated end of term prevalence in the absence of no-mass testing. On the other hand, given low and moderate adherence to other control measures, we would not anticipate reductions in the expected proportion of students infected at the end of term unless carrying out a one-off mass test instance ahead of the final two weeks of the academic term.
Mass testing was either not used (baseline scenario), a single instance took place at the end of week two or week eight of the academic term (corresponding to simulation day numbers 21 and 63, respectively), or regular mass testing was performed on a fortnightly or weekly basis. In each panel, we summarise outputs from 1000 simulations for mass testing covering all eligible students (red), on-campus only (blue), off-campus only (grey). Panels (a-c) compare the distributions of end of term infection prevalence with no mass testing (black) with outcomes for the various mass testing strategies. Panels (d-f) show the average scale of end of term infection prevalence for the given mass testing strategy relative to the scenario where no one-off mass testing event took place. The dashed line signifies parity between the scenarios. We used the following underlying probabilities of adhering to isolation measures: (a,d) 0.2; (b,e) 0.5; (c,f) 0.8. For a listing of values, see Tables S6-S7. End of term prevalence was minimised with a single one-off mass testing instance a fortnight before the term ended.
Overall, at low, moderate and high adherence levels to other SARS-CoV-2 transmission control measures, having a single mass test event towards the end of the academic term increased the likelihood of there being fewer infected students at the end of term compared to the baseline scenario. Regular mass testing, combined with the vast majority of people adhering to other NPIs, was also likely to perform well (Fig. S7, Table S7). Inspection of temporal profiles reveals how, compared to the one-off use of mass testing, regular mass testing flattens the infection curve, whilst simultaneously causing both more individuals to enter isolation and a chance of there being a relatively higher infection prevalence at the conclusion of the academic term (Figs. S8-S10).
Discussion
In this paper, we have described the construction and application of a network model to characterise the transmission of SARS-CoV-2 amongst a student population in a UK campus-based university. Our findings suggest SARS-CoV-2 could readily transmit amongst a student population within a university setting over the course of a single academic term. Maintaining nonpharmaceutical interventions and effective contact tracing curbed transmission, while also reducing the expected time an adhering student would spend in isolation.
Our findings demonstrate the efficacy of isolation and tracing measures in controlling the spread of SARS-CoV-2 if they are broadly adhered to. Reducing the quantity and riskiness of contacts breaks chains of transmission, with the projected potency in the use of nonpharmaceutical interventions to control spread of SARS-CoV-2 at a national scale previously documented [33–35].
Irrespective of adherence probability, we predicted that a higher proportion of the on-campus population would typically be infected compared to those living off-campus. In general, household sizes within on-campus halls of residence are larger than those living in households off-campus. As a consequence, a higher level of mixing is expected, with an associated increased risk of infection; halls of residence have been identified as environments conducive to the transmission of other respiratory illnesses [36]. This outcome reinforces the importance of monitoring the situation in halls of residence, in agreement with prior studies [16].
We also analysed what impact separating on-campus residents who were confirmed infected from household members (for the duration of the infected individual’s isolation period) could have as a potential extra barrier to disease spread. Though we saw marginal improvements compared to not including the intervention, practicalities of the strategy and the outlay on required resources may prohibit it as an implementable option. In particular, there would need to be the spare housing capacity with suitable facilities to accommodate those confirmed infecteds that are living in households with communal bathrooms, and a safe way of moving infectious individuals to the new rooms.
Whilst we found the absolute impacts of running a single mass test across the student population on particular epidemiological measures to be small, it does illustrate the importance the stated objective can have on what is ascertained as the preferred strategy. Based on our modelling framework, if one was looking to minimise the proportion of students infected, then earlier testing with large coverage would be selected. However, an additional concern is the potential risks of asymptomatic students returning home for the winter break and unwittingly spreading infection to their domiciled community. Given an objective of minimising the prevalence of infection at the end of term, then performing the mass test later in the term would be preferable.
Our findings from computational simulations of frequent mass testing strategies are in agreement with prior modelling works indicating that mass testing of students would need to take place at regular intervals, such as fortnightly or weekly, to suppress SARS-CoV-2 transmission [11, 16]. There have been calls that, before universities allow students to return home, community transmission must first be curbed and frequent testing subsequently provided [37]. As an additional aid to help track and monitor the spread of COVID-19 in their student and staff communities, several universities have set up public-facing data dashboards in both the USA [38] and the UK [39].
Where possible, we have taken a data-driven approach to parameterise the system and instruct heterogeneities we expect to be present, such as in student contact patterns. Nevertheless, this work has made simplifying assumptions and our results therefore have limitations. Student numbers and estimates of regional movements between term-time and out-of-term time addresses were taken from pre-pandemic academic years; these movements may not accurately reflect the situation for the 2020/2021 academic year during the COVID-19 pandemic. Additionally, we assumed there would be no students beginning term with COVID-like symptoms, and there was no transmission to students from the wider community. Relaxation of either of these assumptions is likely to generate a larger outbreak throughout the term.
When constructing the contact networks, for simplicity we assumed each student maintained consistent contacts throughout the entire term with others in their household, and selected others from their cohort and the organised societies and sports clubs they were members of. While the assumption for households may reasonably hold, given shared use of communal spaces, one would expect less rigidity in the study and organised social group related contacts. We also used a fixed distribution for drawing random daily social contacts throughout the term, whereas in reality it may be expected the distribution of such contacts to vary temporally. A set of distributions could instead be used to capture these temporal heterogeneities, were the necessary data available to initially discern the amount of time periods warranting a distinct distribution and then subsequently parameterise each distribution. Finally, the level of transmission through this network is contingent on the behaviour of students and their compliance with social distancing measures. We have assumed an uncontrolled reproduction number in the range 2-4 (dependent on the proportion of students that are asymptomatic and the relative transmission rate from asymptomatic infections); unfortunately, the precise value can only be estimated once students return and any emerging outbreak can be measured. In the event of student populations at universities suffering outbreaks, there is scope for the network model framework presented here to be used for real-time parameter estimation. Larger values of R are likely to result in a higher number of cases and greater pressure being exerted on test and trace services earlier in the term.
Multiple refinements of the model structure are still possible and may yield a better understanding of the outbreak impact on the broader university community. We have not included university staff members, or infection to and from the local community. Students with asymptomatic infection interacting with elder individuals in non-COVID secure environments may result in silent transmission of SARS-CoV-2 into more vulnerable groups at risk of severe outcomes from COVID-19. Similarly, given the observed rise with age of the likelihood of severe health outcomes due to COVID-19 disease [7], in the event of widespread community transmission staff and surrounding communities would be likely to experience higher levels of morbidity than students. Another aspect we have not included here is the presence of other respiratory infections. Such an extension would permit the study of test capacity requirements when levels of cough and fever are high due to non-COVID-19 causes, especially of concern in the winter period; were such a scenario to arise it would apply significant stress to the national test and trace system [40].
In the context of the COVID-19 pandemic the movement of students to attend universities, creating large communities of predominately young adults, poses specific challenges in controlling transmission. Infectious disease models may be a useful part of the public health decision-making process, determining the most appropriate interventions to be applied in a university setting. Our work highlights a network modelling approach to capture heterogeneities in contact structure that are particular to the university student population and its projected impact on transmission of SARS-CoV-2. This model suggests that encouraging student adherence with test-trace-and-isolate rules (as well as good social-distancing, mask-use and hygiene practices) is likely to lead to the greatest reduction in cases both during and at the end of term; mass testing is also found to produce strong benefits in terms of reducing infection, generally leading to a greater number of cases being found and isolated.
Author contributions
Conceptualisation
Michael J. Tildesley; Louise Dyson; Matt J. Keeling; Edward M. Hill; Benjamin D. Atkins.
Data curation
Edward M. Hill; Benjamin D. Atkins; Matt J. Keeling; Louise Dyson; Michael J. Tildesley.
Formal analysis
Edward M. Hill; Benjamin D. Atkins.
Funding acquisition
Michael J. Tildesley; Louise Dyson; Matt J. Keeling.
Investigation
Edward M. Hill; Benjamin D. Atkins.
Methodology
Edward M. Hill; Benjamin D. Atkins; Matt J. Keeling; Louise Dyson; Michael J. Tildesley.
Software
Edward M. Hill; Benjamin D. Atkins; Louise Dyson; Michael J. Tildesley.
Supervision
Louise Dyson; Michael J. Tildesley.
Validation
Edward M. Hill; Benjamin D. Atkins; Louise Dyson; Michael J. Tildesley.
Visualisation
Edward M. Hill; Benjamin D. Atkins.
Writing - original draft
Edward M. Hill.
Writing - review & editing
Edward M. Hill; Benjamin D. Atkins; Matt J. Keeling; Louise Dyson; Michael J. Tildesley.
Financial disclosure
This work has been supported by the Engineering and Physical Sciences Research Council through the MathSys CDT [grant number EP/S022244/1] and by the Medical Research Council through the COVID-19 Rapid Response Rolling Call [grant number MR/V009761/1]. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data availability
Summary data that were used to perform the study are publicly available or stated within the main manuscript and Supporting Information.
Code for the study is available at: https://github.com/EdMHill/covid19 uni network model.
Competing interests
All authors declare that they have no competing interests.
Supporting information items
Supporting Text S1: Off-campus student household size
Estimation of an off-campus student household size distribution from the Social Contact Survey data.
Supporting Text S2: Cohort data
Outline of data underpinning the partitioning of the student population into different study cohorts.
Supporting Text S3: Parameterisation of contact risk
Summary of the use of contact survey data to estimate the relative transmission risk across contacts between students occurring in household versus non-household settings.
Supporting Text S4: Non-intervention scenario calibration
Overview of simulation outputs in the absence of any interventions.
Supporting Text S5: Initial seeding of infected and recovered individuals
Description of the method applied to estimate the expected number of students in each COVID-19 disease state at the beginning of the 2020/2021 academic year.
Additional tables
Summary statistics to support the displayed figures.
Additional figures
Supplementary mass testing scenario results.
Footnotes
We found errors in the calibration process using the no intervention scenario that had led to a lower early Rt than intended. We have addressed that issue and updated the results. We have also extended the ranges of the Uniform distributions for the asymptomatic variables.