Summary
Background The unprecedented rapid development of vaccines against the SARS-CoV-2 virus creates in itself a new challenge for governments and health authorities: the effective vaccination of large numbers of people in a short time and, possibly, with shortage of vaccine doses. To whom vaccinate first and in what sequence, if any at all, to avoid the most fatalities remains an open question.
Methods A compartmental model considering age-related groups was developed to evaluate and compare vaccine distribution strategies in terms of the total avoidable fatalities. Population groups are established based on relevant differences in mortality (due to e.g. their age) and risk-related traits (such as their behaviour and number of daily person-to-person interactions). Vaccination distribution strategies were evaluated for different vaccine effectiveness levels and population coverage in a case study for Spain.
Findings Our results unambiguously show that planning vaccination by priority groups can achieve dramatic reductions in total fatalities compared to no prioritisation. Our results also indicate that the best strategy for vaccine distributions appears to be to prioritise groups with the highest number of daily person-to-person interactions. This is due to the importance of the avoided subsequent infections inflicted on the rest of the population by those in those groups.
Interpretation These results are in direct contradiction with several published guidelines for COVID-19 vaccination and therefore highlight the importance of conducting an open comprehensive and thorough analysis of this problem leaving behind possible preconceptions.
Introduction
COVID-19 has inflicted great stress worldwide with more than 45 million cases and over one million deaths globally at the end of October, 2020. (1,2). The pandemic is not near its end and the disease will probably not go away, becoming endemic in many regions throughout the world. In this scenario, the development of adequate vaccines is an alternative for primary prevention of the disease, so far implemented through hygiene, massive testing and isolation, social distancing, and quarantine.
Vaccines, of different types, are products of biotechnological processes which serve two functions: to protect the individual from contracting the disease and to stop the transmission of the disease (3). The development and approval of vaccines is long, taking on average several years (4). This was the rule until now: an unprecedented global effort from pharma and academia, supported by government and private organizations, has made possible that one or more COVID-19 vaccines may become available during early 2021 (5). Given the tremendous speed with which COVID-19 vaccines are being approved and trials implemented, it is highly probable that one or more vaccines will become available soon.
With more than 320 candidates and 76 trials now underway (15 in phase I; 25 in phase I/II; 4 in phase II; 2 in phase II/III; and 13 in phase III), registered at ClinicalTrials.gov, the next problems to sort out will probably be mass production of the vaccine and how to allocate the available vaccines to potential users (6,7).
The WHO issued a draft statement on September 9th, 2020, addressing issues related to the fair allocation of vaccines for countries around the world. Available doses of COVID-19 vaccines worldwide are proposed to be managed centrally and equitably by the COVAX Access Mechanism, a coalition of member countries together with the ACT-Accelerator Collaboration (WHO; the Bill & Melinda Gates Foundation; Gavi, the Vaccine Alliance; the Global Fund; the Coalition for Epidemic Preparedness Innovations -CEPI; and Welcome Trust) (8) to allow fair allocation of available vaccines. The COVAX initiative (8) proposes vaccine doses for each country to cover 3% to 20% of the population proportionally to each country. There are however some small, high income countries that may be capable of securing vaccine doses for their entire population at early stages too.
Despite the estimated and unprecedented fast production of vaccines, the number of vaccines initially available will be insufficient, due to the fact that the vast majority of the population worldwide is still susceptible to the infection. There is no doubt that vaccine uptake will be an important driver (9) however, intra-country capacity for adequate vaccine distribution will be essential and will most likely impact the final amount of deaths related to COVID-19 (10). Some of the important drivers for vaccine allocation seem to rise from ethical principles (11,12). For instance, these ethical principles may point towards first, reducing premature deaths; then, reducing economic and social serious deprivations and last, focus on return to functional populations and societies (13). However, as disputed the order and scope of these principles may be, the immediate need of decreasing COVID-19 deaths (direct and indirect) that may be avoidable, should be the first priority.
Decisions based on empirical observations are a luxury not always possible during a pandemic and mathematical modelling provides a tool to guide immediate decisions. Although several epidemic models for the COVID-19 outbreak have been developed to forecast the extent of the pandemic or the impact of interventions for different regions (14–21), any predictive mathematical model has limitations, which are inherent to the model itself but also to the quality of the input data. Models can lead to great predictive failures (22) however they can also serve as valuable tools to better understand nontrivial underlying interactions in complex processes and to comparatively evaluate public health strategies.
Best vaccine distribution strategies help decrease the number of fatalities by protecting the groups at risk directly (via vaccination of the individuals that belong to those groups of risk) and indirectly (via vaccination of individuals that are most in contact with those at risk) (23). Vaccination itself changes the characteristics of the population in real-time, changing the probability of death of different groups as time elapses throughout the vaccination campaigns. Considering this, a fixed approach (e.g. vaccinating a particular population group) during a prolonged amount of time as opposed to a dynamic changing adaptive approach, might not produce the best possible results in averting the highest potential number of preventable deaths by vaccination. Dynamic models can be used to inform which group should be vaccinated and at which moment of the vaccination campaign while accounting for the changing characteristics of the population due to the vaccination itself.
If we consider that vaccination has the indirect benefit of decreasing transmission, thereby reducing the infection risk also to those who have not been vaccinated, optimum strategies for vaccine allocation can become counterintuitive and complex. Existing past studies for influenza have already shown how targeting the vaccination of lower-risk and high-transmission groups first may achieve superior results (24).
To date only a limited number of preprint studies have focused on the model-based evaluation of vaccination strategies for SARS-CoV-2 (25–27). In this work, a new COVID-19 SEIR-type model, segregated by population groups, based on that by (19), is applied to evaluate and compare vaccine distribution strategies in terms of what group prioritisation should be followed for vaccine distribution. Although slightly different optimisation goals are possible, the minimum total final fatalities after the vaccination campaign and outbreak is the pursued goal. Several example scenarios using demographic and epidemiological data from Spain are evaluated.
Research in context
Evidence before this study
We have searched in PubMed, Google and medRxiv for publications and preprints. Search terms used were (“Vaccine”) AND (“COVID-19” OR “SARS-CoV-2”) AND (“model”). Publications using epidemic models that target vaccination strategies are somehow scarce. The search returned a paper in PLOS One (addressing the H1-N1 outbreak), one in Nonlinear Science and Numerical Simulation that we considered not applicable to this case. The search also returned a article in Science that addressed vaccination in previous pandemics. That work stated that the 1957 outbreak was similar than COVID-19 as it affected mostly elders. The optimal vaccine distribution for that outbreak appeared to prioritise first schoolchildren and adults from 30-39 years old in order to decrease the number of fatalities. A publication from Infectious Disease Modelling evaluated the application of a vaccine but did not consider age distribution and the transmission factor between groups. Four medRxiv preprints attempted to address the issue of the vaccination strategies for COVID-19, with diverging outcomes between studies. One of those studies evaluated the vaccine effectiveness required to mitigate substantially the pandemic and also its allocation as a function of the effectiveness. An alternative work indicated that adults over 60 years old should be targeted first in case that vaccines do not block transmission. The third work stated that it was a better strategy to vaccinate elders first. The fourth preprint considered that in function of the immunity at the time in the population, vaccination that targets transmissions can be more effective if there is sufficient natural immunity in the population.
Added value of this study
This study is one of the first to apply an epidemic model of the COVID-19 disease segregated by age-related population groups to evaluate and compare vaccine distribution strategies. The alternative strategies compared included priorities by mortality, by number of interactions and a combination of both as well as no priority at all. We evaluate two different vaccine deployment scenarios: one limited by the logistics of the vaccination rate assuming no shortage of vaccine doses and the other limited available vaccine doses. In the majority of the numerous scenarios simulated for different vaccine effectiveness, population coverage and doses available, significant reductions of fatalities are predicted if the population groups with the most interactions are targeted first. Counterintuitively, a vaccine distribution strategy to vaccinate first the groups by highest mortality and lower interactions leads to higher number of fatalities. All these results assume that the vaccine is able to both protect the individual and to block the transmission of the virus.
Implications of all the available evidence
The evidence found suggests that, in contrary to conventional wisdom, that vaccinating those with the most interactions first instead of those with the highest mortality is more effective in order to avoid more fatalities (including those among the most vulnerable). Further work to confirm vaccine effectiveness against transmission as well as more accurate contacts matrix via contact tracing applications or surveys will increase the confidence on these results.
Dynamic COVID-19 vaccination model
Based on our previous work (19) a model was developed specifically for the optimum vaccine allocation problem at hand. A complete description of the model is provided in the Supplementary Information, Section I.
The model allocates individuals in the population in compartments by population groups and by infection or disease severity stage. In order to minimise uncertainty and to ensure maximum utilisation of information (either available or measurable) the population groups are defined based on meaningful differences both epidemiological (in severity and mortality) and of behaviour or activity traits that affect their risk of infection. These later could include traits such as their number and type (with which other groups) of daily contacts, their level of self awareness and protection attitudes. The population groups segregation can be related to their age but also to any other arbitrary classification based on these epidemiological and behavioural differences. Groups such as front line workers, individuals with a very high risk of mortality etc could be grouped separately. The most suitable groups definition may differ and be country or region specific however group-specific reliable data will always be required and that poses limitations to the number and types of groups.
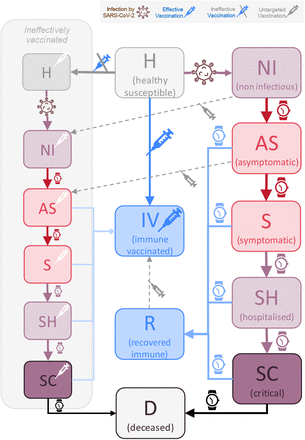
Individuals in the population are allocated to only one group that they never abandon while they can transition through infection and disease severity stages. Figure 1 provides an overview of these different stages and transitions, disease severity progression and vaccination govern the transitions of individuals between disease stages. The rates of infection are calculated as shown in Figure 2. Vaccination causes individuals to transition either to vaccinated immune or to ineffectively vaccinated non-immune stages. Most parameters involved on the disease transitions are either already available from recent clinical and/or epidemiological information (see Supplementary Information section III). All other parameters are also mechanistic and can be interpreted, behaviour related parameters can be surveyed for among the target populations or communities. A complete reproducible description of the equations, variables and parameters of the model is provided in the Supplementary Information sections I-V.
Schematic representation of the model compartments in terms of infection and disease severity stages. Infection can only occur by contact of healthy susceptible individuals with infectious either asymptomatic or symptomatic individuals (red boxes). Individuals spend in each stage an average amount of time depending on their transition path towards recovery or increased severity. Vaccination, if effective, avoids infection and transmission and places individuals at immune vaccinated stage. Ineffective vaccination maintains individuals in their disease stage although accounted separately as already vaccinated.
The rate of infection of heathy susceptible individuals from a group i (see also Eq. S1.4) is the sum of the infections by asymptomatic and symptomatic individuals from all other j groups.
Model limitations and assumptions
Although the model was specifically developed for the optimum vaccination problem at hand, it shares many of the fundamental characteristics of compartment SEIR-type models as well as their limitations. As for the case of our earlier model (19), this type of models consider all individuals located in a common single domain or closed community. Since no geographical clustering or separation, neither any form of migration in or out of the community are captured, large cities with ample use of public transportation remain the best described by this and other SEIR-type disease propagation models.
In these models, variables and parameters refer to representative averages for each compartment stage and population group. These characteristics may limit the model representation of non-linear relevant phenomena that may occur in the real-world that could be better described by agent-based models. Examples of these include phenomena such as the so-called super spread events or other location specific phenomena that cannot be described by SEIR-type models. Any quantitative application of this model and any other model for prediction purposes in public health must always be accompanied by a critical discussion against these limitations (28).
In addition to the above, other specific assumptions in this model, that are of special relevance to the vaccination problem at hand, include:
✓ All ever-infected individuals that recover become fully immune, irrespective of their severity path, and cannot be infected or infectious again. Reinfections are not modelled in this work.
✓ The vaccine effectiveness is considered the same both against infection and transmission. This can be revised in future model versions as specific information on effectiveness against transmission becomes available for the upcoming vaccines.
✓ No differences are considered in immunity, or any other epidemiological aspect, between individuals ineffectively vaccinated and those never vaccinated.
✓ Recovered individuals (aware or not) as well as infected and asymptomatic unaware individuals are equally eligible for vaccination as those healthy susceptible.
✓ If multiple groups are called for vaccination simultaneously, their rates of vaccination are proportional to the groups relative sizes in terms of their eligible unvaccinated individuals. The total vaccination rate will match the logistic rate limit set by the capacity of the health system or by the availability of vaccine doses.
R-based projected avoidable deaths (RbPAD) method for vaccine distribution
A plethora of optimisation methods can be attempted to find the best possible vaccination strategies. A computationally inexpensive, model independent method was developed in this work specifically for the vaccine distribution problem.
The R-based Projected Avoidable Deaths (RbPAD) method, fully described in the Supplementary Information section VI, is based on the estimation at each moment of the projected avoidable deaths (PAD) per vaccination in each group using the R number and the group’s own mortality. The method allocates priority dynamically to the group i with the highest PAD number per vaccination. The PAD are calculated as function of three elements, namely (i) the risk of infection in that group (as the ratio of the present rate of infections and the number of individuals in the group); (ii) the mortality per infection in the group (fd_nii) (from epidemiological data) and (iii) the mortalities of the projected secondary and subsequent infections avoided that a vaccinated group member would have inflicted on the entire population (obtained via estimated R matrix).
Evaluation of vaccine distribution strategies: Case for Spain
Although the model is capable of evaluating complex combined scenarios simultaneously involving interventions (such as isolation of specific groups) and vaccine distribution strategies, only the later are evaluated here. Five different strategies for vaccine distribution by population groups are compared for a case using population demographics and epidemiological data from Spain, namely:
No group prioritisation: all population in all groups is called for vaccination in equal terms.
Priority to the groups with the highest mortality per infection (from highest to lowest). Groups are called one by one and only once (single call) until coverage for each group is reached.
Priority to the groups with the highest number of interactions (daily contacts) (from highest to lowest). Groups are called one by one and only once (single call) until coverage is reached.
R-based projected avoidable deaths (RbPAD) criteria. Groups can be called multiple times with flexibility partial group vaccination in each call.
The best of all the possible sequences of groups priority. All possible permutation of the groups are evaluated assuming single calls i.e. they are called one by one and only once. This approach requires intensive computation (9! = 362,880 simulations)
Model implementation for Spain
In the example evaluated for Spain, population groups were defined by (age-related) activity as namely: preschool children (ages 0-4); school children (ages 5-14); higher school and university young (ages 15-24), young workers (ages 25-49); mature workers (ages 50-59); senior workers (ages 60-64); early retired (ages 65-69); retired (ages 70-79); elderly (ages 80+). This definition of groups is partly arbitrary but based on the criteria of meaningful differences in mortality and behaviour that impact the problem at hand.
In the model individuals never leave the (age-related) population group to which they belong and, at a given time, they sit on one of the possible infection stages. These stages are defined in terms of infectiousness and severity of symptoms analogously as in (19), namely: healthy susceptible (H); infected non-symptomatic non-infectious (NI); asymptomatic infectious (AS); symptomatic infectious (S); in need of hospitalisation (SH); in need of critical care (SC); recovered immune (R) and deceased (D), in addition, those effectively vaccinated become vaccinated immune (IV). Individuals ineffectively vaccinated (i.e. the vaccine does not immunise them against infection, severity or transmission) maintain their current stage and they are simply accounted separately as already vaccinated (see Figure 1).
Two types of vaccine distribution scenarios are presented, namely (i) distribution limited by the logistic rate of vaccination (no shortage of doses) and (ii) vaccination limited by available doses. The parameters shown in Table S3.1 and Tables S5.1-2 were used. The example scenario was selected with following initial conditions and assumptions:
▪ No initially immune individuals.
▪ No initially vaccinated individuals nor fatalities.
▪ Initial case incidence is set as of 0.1% for NI and S and 0.3% for AS respect to the entire population, equivalent to 500 active cases per 100,000 population)
▪ All other individuals initially considered as healthy susceptible (H).
▪ A total population of 47,026,208 as for Spain in 2019 is considered.
▪ Constant rate of vaccination of 1% of the population per day until campaign ends.
▪ Different vaccine effectiveness and maximum population coverage values are evaluated.
Distribution under limited logistic rate of vaccination (no shortage of doses)
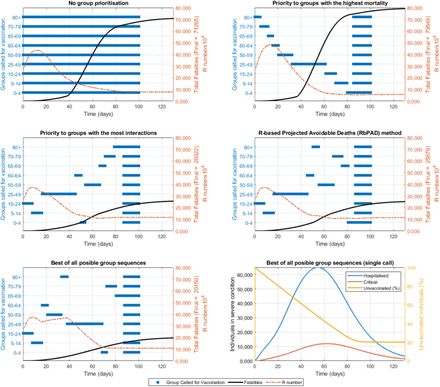
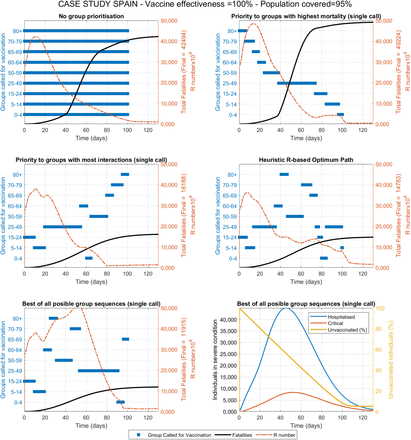
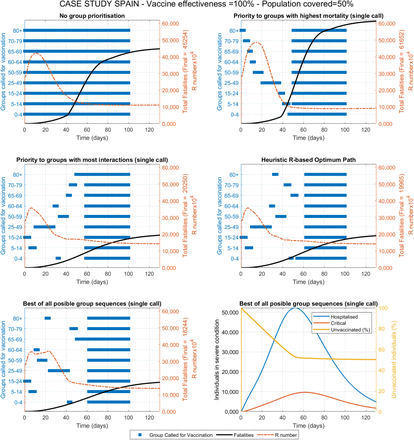
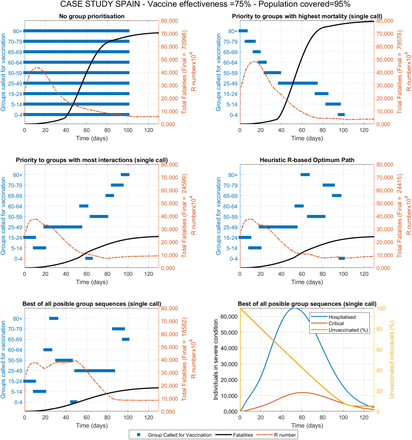
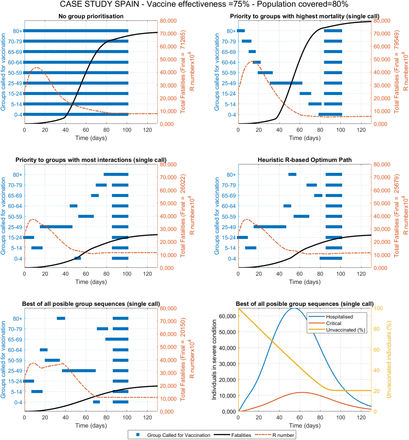
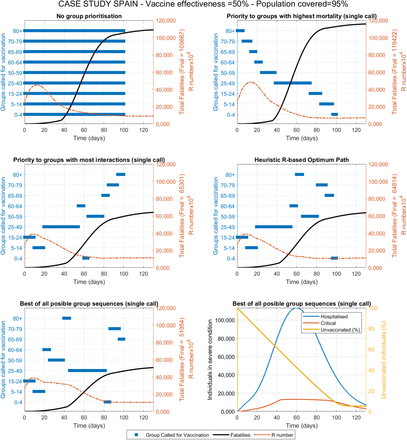
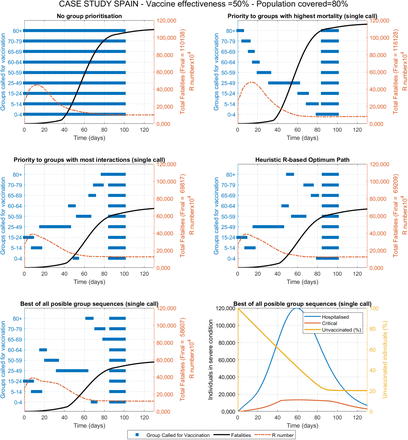
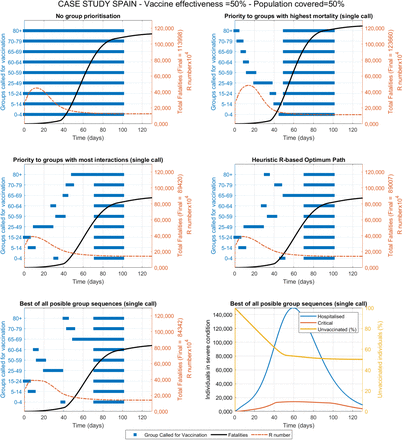
The first scenario evaluates the vaccine distribution as fast as logistically possible considering that sufficient doses are available. This could represent the case of small countries that may have access to sufficient doses for their entire population in early stages. Figure 3 shows the results obtained under each of the five strategies, in terms of proposed sequence of priority groups for vaccination as well as the progression in total fatalities and the R number with time. A value of vaccine effectiveness of 75% and a maximum population coverage of 80% is used as reference. Vaccines effectiveness is defined as the proportion of vaccinated individuals who become immune and non-transmitters. Population coverage is defined as the maximum percentage of the population that can be reached and accepts the vaccine. A summary of the results obtained for nine combinations of these two parameters is presented in Table 1.
Performance results of different strategies for vaccine distribution at different vaccine effectiveness and coverage of the population.
Compared vaccination strategies under no limitation of available doses. Active groups called for vaccination, fatalities and R value over time are shown for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness is 75% and population coverage is 80%. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive RbPAD strategy is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
The different strategies proposed lead to very significantly different outcomes in terms of fatalities respect to the base case of no group prioritisation. If a strategy based on priority to the groups with the highest mortality is followed, the predicted total number of fatalities appears to increase moderately (∼12% higher). On the contrary, if priority is established to those groups with the most interactions (from highest to lowest), dramatic reductions in fatalities (∼63% lower) are predicted (Table 1). If the optimum strategy is further refined using the RbPAD method, which would require of no model for its practical implementation, additional smaller improvements appear to be achieved. Intensive computational evaluation of all possible permutations of the nine groups (for single group calls) provided the best result (∼72% lower number of fatalities). The differences between the strategies by most interactions, RbPAD and all possible permutations differ very little suggesting that it is the number of daily interactions that individuals from each have what contributes the most to the results. This trend of differences between the strategies remains consistent for the three different vaccine effectiveness and population coverage values (Table 1). The detailed simulation results for of these different scenarios are presented in the Supplementary Information section VII in Figures S7.1-9.
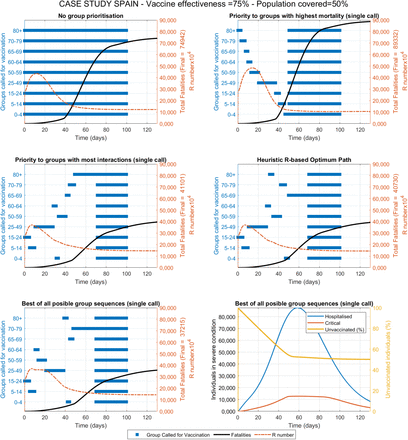
Distribution under limited availability of vaccine doses
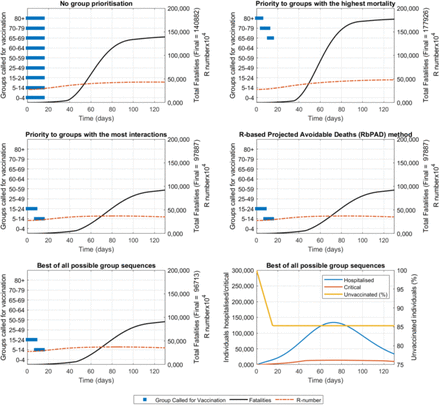
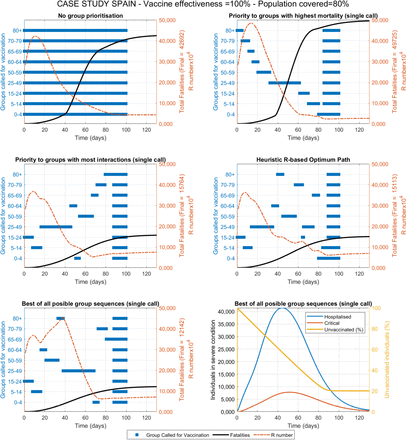
The second scenario evaluates the vaccine fast distribution considering vaccine shortage. This is the case expected for most countries including those partaking in the COVAX Access Mechanism. Figure 4 shows the results obtained for each of the five vaccine distribution strategies, for a vaccine effectiveness of 75% and assuming vaccine doses available for only 15% of the population. A summary of the results obtained for twelve combinations of these two parameters is presented in Table 2.
Performance results of different strategies for vaccine distribution at different vaccine effectiveness and availability of doses.
Compared vaccination strategies under limited available doses to 15% of the total population. Active groups called for vaccination, fatalities and R value over time are shown for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness is 75% and population coverage is 80%. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive RbPAD strategy is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
The results under vaccine shortage are equivalent to those under no shortage and indicate that, for different effectiveness and availabilities of the vaccine, again the vaccine distribution first to those groups with the most interactions provides the largest reductions in fatalities. Under this scenario of vaccine shortage the RbPAD method performed slightly worse in some cases that a pure allocation my number of interactions (Table 2). The RbPAD method uses the R number to project subsequent avoided infections which may be a less accurate predictor in some of these cases.
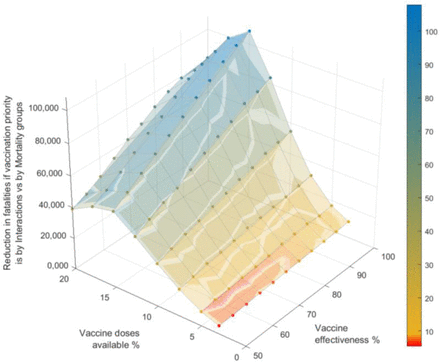
Figure 5 displays the differences in total final fatalities between a vaccination under a groups interactions criteria vs. a groups mortality criteria for different vaccine availability and vaccine effectiveness numbers. For vaccine availabilities over 5% the potential for avoided fatalities becomes already very significant when vaccine distribution is prioritised to the most interactive groups.
Effect of different vaccine availability and effectiveness values on the number of avoidable fatalities if the vaccination is distributed with priority to those from highest to lowest daily interactions respect to if it is distributed by highest to lowest mortality. Numbers are for the case study example presented for Spain (47M population).
The above results for both scenarios, without and with vaccine doses limitation, strongly indicate that, independently from the availability of a calibrated model and of high-end computational resources, the strategy to prioritise population groups with the most interactions (or a similar, more refined, sequence as proposed by the RbPAD method) can achieve enormous reductions in total fatalities at the end of the vaccination campaign. In all cases vaccine distribution to the highest mortality (oldest) groups first, leads to increases in total fatalities respect to even doing no prioritisation at all.
Impact of the behavioural parameters
The main epidemiological model parameters involve the fractions of individuals progressing in severity and recovering, as well as the average times in each disease stage. These have been taken from literature good estimations based on latest data that becomes more and more accurate as we learn more about the SARS-CoV2 virus. Their values can be updated as new information comes in but their degree of uncertainty is relatively small.
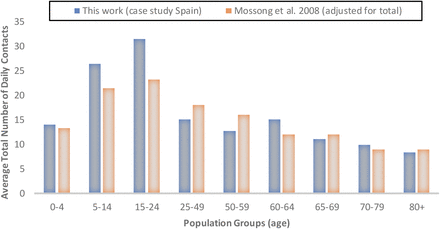
The model uses also behavioural parameters in order to simulate infection rates, two types of these parameters have great impact on the model results. The first type are the number of daily contacts (ni) that individuals in each group have with the other groups. This is defined using a contacts matrix such as the one in the example for Spain shown Table S5.1 in the Supplementary Information. The values used do not differ substantially from those reported in literature on social contacts (30) (see Figure S5.1).
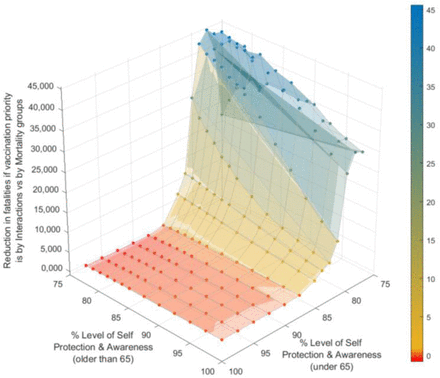
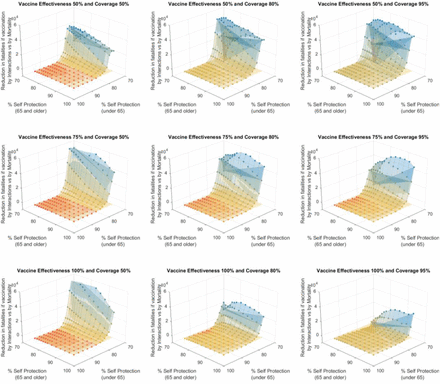
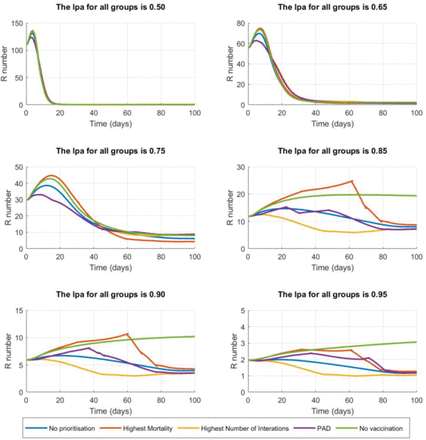
The second important type of behavioural parameters are the levels of self protection and awareness (lpa), used in this model to estimate the likelihood of infection when a contact between a susceptible and an infectious individual takes place. These parameters, in this model, are a simple one-number description incorporating habits such as the use of mask, social distancing, general attitude and awareness to protect oneself and others and therefore these are the parameters with the largest uncertainty. Although the values provided have been estimated such that the model calculated R values across the simulations correspond to values that have been reported (see Supplementary Information section IX), the uncertainty in these lpa parameters remains very high. In order to reduce this uncertainty and its propagation to the vaccination strategy results, a sensitivity analysis of the impact of different levels of self protection and awareness (lpa) between those under and over 65 years of age was conducted. For the case of vaccination without shortage of dosages, Figure 6 displays the differences in total final fatalities between a vaccination strategy with priority by groups interactions criteria vs. by groups mortality criteria for different levels of self protection and awareness for the younger and older than 65. Full results for the different vaccine effectiveness and coverage values are shown in Figure S8.1 in the Supplementary information.
Impact of the different levels of self protection and awareness (for those under 65 and those over 65 years of age) on the number of possible fatalities that can be avoided if the vaccination is distributed with priority to those from highest to lowest daily interactions respect to if it is distributed by highest to lowest mortality. Numbers are for the case study example presented for Spain (47M population), no shortage of vaccine doses vaccine effectiveness of 75% and population coverage of 80%.
These results clearly show a very significant and asymmetric potential gain in terms of avoided fatalities if the most interactive groups are vaccinated first for low levels of self protection and awareness (e.g. PPE use and distancing compliance) by the younger (and more interactive) groups. On the other hand, only minor gains could be attained by vaccinating those with highest mortalities and low interactions first and only under at very high levels of awareness and PPE compliance.
Conclusions
The dynamic deterministic model developed, describing individuals in (age-related) population groups and disease stages, can be applied to the evaluation of vaccination strategies. The model results appear to describe expected trends and allow for mechanistic interpretations to draw hypotheses and conclusions that can inform public health policy.
Our simulation results, based on the model developed, strongly indicate that a planned vaccine distribution, following prioritised sequences of population groups, can achieve enormous reductions is the total final number of fatalities. Based on the results, group prioritisation criteria based on mortality is not recommended. Both for vaccination scenarios without and with vaccine doses shortage, a prioritisation of the groups with the highest number of daily interactions (person-to-person contacts) appears to lead to great reductions in the final number of fatalities. The model-independent R-based projected avoidable deaths (RbPAD) method developed in this work achieves moderate further improvements on the final number of fatalities in most cases. Both these strategies’ fatality reductions do not differ much from that achieved by the best among all possible group priority sequence (after model-based computationally-intensive evaluation of all possibilities). These results contradict directly recently published recommendations and suggest that a thorough model-based analyses and reconsiderations of vaccine distribution strategies against the SARS-CoV-2 may be required.
Contributors
JR conceived, developed the model, designed the experiments and supervised the study, JR and MP analysed the model results. JR and MP did the computational analysis and prepared all figures. JMA, JR and MP collected, processed, analysed and contributed data. JR, MP and JMA drafted the original Article. All authors contributed to the editing of the Article. All authors read and approved the final Article.
Supplementary information
Supplementary Section I. Dynamic COVID-19 model for vaccination
The definition of the model dynamic (state) variables is shown in Table S1.1. Each variable corresponds to the number of individuals in that stage in a vector per (age-related) population group (9 activity groups as defined above). Under this structure, each dynamic variable is a vector of dimension 1×9, and the total number of states is a matrix of dimensions 15×9 (15 stages and 9 population groups). Vector variables and parameters are represented in bold font and scalar ones in regular font across all the manuscript.
Model dynamic variables accounting for the number of individuals in each infection stage and group.
Rates of transition between infection stages
The progression of individuals across stages, as illustrated in Figure 1, includes the impact of vaccination bringing individuals directly into an immune stage or, if ineffectively vaccinated, remaining in their current stage. The transitions between stages are governed by the rates of infection, disease transition and vaccination shown in Table S1.2. All the rates are in vectors with each element corresponding to the rate for each age-related population group.
The average rates of transition between stages are defined as per the latest epidemiological and clinical data and they can be updated as knowledge of the disease increases and treatments improve. These parameters include the proportion of individuals that transition to a more severe stage or recover (Table S1.3) and the average times reported at each stage before transition or recovery (Table S1.4).
Rates of infection and transition between states in vectors per population group.
Fractions of individuals progressing through each severity stage per population group.
Clinical average times in each infection stage in vectors per population group.
The rates of transition between stages (in number of individuals per day) are described in Eqs. A1.a-e. All rates are vectors per age group of dimensions (1×9). Note that the point operators between vectors indicate an element-by-element vector operation.





The rates of individuals fully recovering and becoming immune from the different infected stages (in number of individuals per day) are described in Eqs S1.2.a-e. (all rates in vectors per age group).





The rate of transition from critical to deceased is the sum of that of those in critical condition receiving intensive care (rd_scic) plus that of those without available care (rd_scnc) as per Eqs. A3.a-c. All critical individuals not receiving intensive care (Nsc_ncc) are assumed to become fatalities after a time (td_nc). A description of the critical care model allocation (in case the ICU capacity limits is reached) is provided below.
 where
where


Allocation of critical care capacity if exceeded
The impact of available critical care capacity is modelled by a specific function to allocate critically ill individuals as per the available ICU. The function allocates critically ill individuals in two possible groups, namely those admitted to ICU (Nsc_ic) and those not admitted to ICU due to lack of capacity or for medical or humanitarian reasons (Nsc_ncc). At each simulation time point the allocation function is computed for the total Nsc per age group.
The function allocates ICU resources with priority to populations groups with higher ICU survival rate (fr_sc) until the maximum number of intensive care units is reached leaving any remaining individuals without care, in this way Nsc_ic and Nsc_ncc are computed.
As the COVID-19 outbreak has progressed, data indicate that not all patients in critical condition have been admitted into intensive care units (ICU). Data show that many individuals with very poor prognosis, particularly those of oldest age may have never been referred to ICU due to capacity limitations or other medical humanitarian reasons. Data from Spain (29) show that for individuals over 70, only a fraction of the reported fatalities previously hospitalised was ever admitted to ICU and this may not be only due to ICU lack of capacity. In order to maintain consistency with the reported data (29) the parameters of fd_sc and fsc_sh have been estimated such that the product of fd_sc * fsc_sh (fatality ratios over hospitalised individuals) is consistent with reported numbers for all ages irrespective of reported ICU admissions.
Rates of infection
The infection of healthy susceptible individuals (H and HV) is modelled as occurring only via their interaction with infectious either asymptomatic (AS) or symptomatic (S) individuals. Hospitalised (SH) and critical (SC) individuals are assumed not available for contacts neither are those deceased (D). Immune individuals after recovery (IR) or effective vaccination (IV) are also not infectious but contribute to the interactive pool of individuals towards herd immunity.
Two rates of infection of healthy susceptible individuals (in number of infections per day) are defined, one from each one of the two possible infecting groups (AS and S). However, in order to serve the goal of determining the optimal sequence of vaccination through population groups, the rates of infection have been expanded into terms for each population group.
The rate of infection of each (age-related) population group i results from the product of the number of healthy susceptible (H) individuals in the group (Nh i) times the sum of the rates of infection from contacts with each one of all the groups. This, for each group, is the product of the average number of daily contacts with individuals of that group (nih i,j) times the fraction of those in that group which are infectious (AS or S) times the likelihood of contagion to occur (modelled as function of the use of protection measures e.g. PPE by individuals in i and j groups) (see Eqs S1.4.a-b).


For each (age-related) group, the average number of daily contacts an individual in a group i has with individuals from each one of the groups j (nii,j) are the most important parameters required as an input as they describe the level of social interactivity. These inputs allow for the description of specific key activities in a given group as well as for a complete customisation to the specifics of any community or country. Previous estimations and recent data from contact tracing applications and modelling makes the use of these information possible and reliable in terms of these parameters (30,31). Examples on how these parameters reflect interventions is the opening of schools, which would involve high numbers of daily contacts between children in schools age groups, similarly for secondary school or universities but not necessarily with the other groups. This mapping of contacts is provided via a contacts matrix, in which only the part above the diagonal can be provided as direct input while the part below the diagonal is automatically calculated for consistency between groups based on their relative population sizes. Table S3b shows an example of values arbitrarily assigned and using the demographics of Spain 2019 (32). Interventions such as the degree of social isolation as described by (19) remain possible to simulate by modification of these matrix of average daily contacts even at a more detailed level since specific values for group-to-group number of daily contacts can be defined.
The second term impacting the rate of infection of a group i is, for each j group with which contacts exist, the proportion of individuals that are infectious (i.e. AS and S) and still interacting (f iasj and fisj). This can be directly computed at every time step from the dynamic variables (Eq. S1.5). This computation incorporates the impact of the awareness of infection after positive testing (19) via a reduction factor of social interaction for those infected-aware (due to positive testing) or of infected-suspicious individuals. For untested individuals in a group j showing symptoms (S), a precautionary self or imposed partial quarantine is captured by the parameter (rfi sj). For tested individuals, the awareness of infection after a positive result is assumed to lead to a full quarantine and removes those individuals from regular interaction with others. The fractions of infectious AS and S individuals that remain in interaction with others (fias and fis) are calculated as per Eqs S1.5.a-b. Hospitalised, critical and deceased are considered excluded from the pool of interacting individuals.
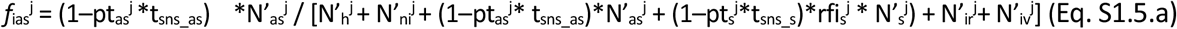
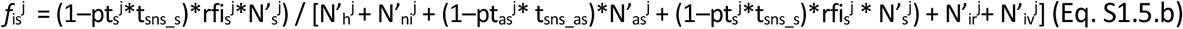 where, N’xj means the sum in stage x of both those not vaccinated and those ineffectively vaccinated (N’Xj = Nxj + Nxvj) in population group j; ptasj is the proportion of randomly tested non-symptomatic individuals and ptsj is the proportion of symptomatic individuals tested. The parameters tsns_as and tsns_s refer to the sensitivity of the tests for individuals in AS and S stages respectively. The differences are justified since e.g. for non-symptomatic individuals, only RT-qPCR tests are typically assumed adequate while, for symptomatic S individuals, both RT-qPCR and serological tests are used.
where, N’xj means the sum in stage x of both those not vaccinated and those ineffectively vaccinated (N’Xj = Nxj + Nxvj) in population group j; ptasj is the proportion of randomly tested non-symptomatic individuals and ptsj is the proportion of symptomatic individuals tested. The parameters tsns_as and tsns_s refer to the sensitivity of the tests for individuals in AS and S stages respectively. The differences are justified since e.g. for non-symptomatic individuals, only RT-qPCR tests are typically assumed adequate while, for symptomatic S individuals, both RT-qPCR and serological tests are used.
The third term impacting the rate of infection within group i, is the likelihood of infection per contact with an infectious (AS or S) individual of the group j. This is an element that could be directly provided in the form of matrix of likelihood of infection between groups (pi_as and pi_s) without further modelling. If the effect of specific interventions if of interest, the likelihood of infection can be further modelled in more detail as per below.
In this example likelihood of infection between groups is presented modelled as per Eq. S1.6a-b based on the level of PPE use and awareness displayed by the two interacting (19) (see Eqs. A6) together with a newly proposed degree of infectiousness for AS and S. The parameters infas and infs reflect the degree of infectiousness between 0 and 1. This degree of infectiousness is considered potentially relevant in view not only on possible differences in viral load between AS and S individuals but also of ongoing research regarding specific population groups (e.g. children) which could display different levels of infectiousness to others. The level of protection and awareness of healthy susceptible individuals in the group i is described by the parameter lpahi as they interact with infectious AS and S individuals of group j with lpaasj and lpasj respectively. The values of the parameters can vary between 0 and 1, with 1 corresponding to the use of comprehensive protective measures and zero to the most careless opposite situation. Different values are assigned for the different activity and age-related population groups. (e.g. for primary school children and elderly).
In this way, for individuals in group i, the likelihood of infection per interaction with individuals of the group j (AS and S respectively) is calculated as per Eqs S1.6.a-b.


Table S1.5 shows the definitions and units of key variables and parameter used in the calculation of the rate of infection.
Behaviour-related variables and parameters affecting the rate of infection.
Rate of vaccination
Once an effective vaccination against the SARS-CoV-2 virus becomes available, its mass deployment will take place, at any given moment, at a specific vaccination rate. This rate will be limited either by the availability of vaccine doses or by the system’s capacity to deliver them.
The recipients of the vaccine within the population groups will be all those individuals, either non tested or having tested (truly or falsely) negative or having recovered, that display no symptoms. This will include the vaccinations to the target healthy individuals (H) but also to untargeted individuals such as the non infectious (NI), those unaware (untested or with false negative test) that are asymptomatic infectious (AS) and those that have recovered from the infection (aware or not) (R).
A total capacity vaccination rate is defined (rvT), in number of individuals that can be vaccinated per day. The vaccination rates of individuals in each of the four possible stages suitable for vaccination, are defined as per Eqs S1.7.a-d in vectors for each (age-related) population group. The rate is proportional to the individuals in each stage and in each group among those suitable and called for vaccination.
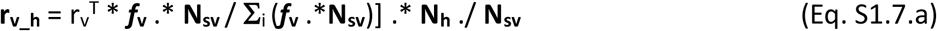
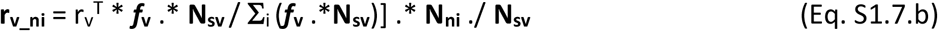
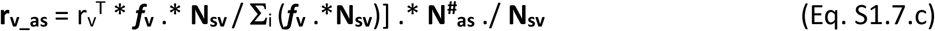
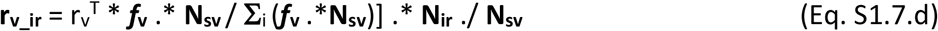 where fv is a vector of zeros with one only on the groups currently called for vaccination in a specific moment. N#as refers to untested AS individuals therefore unaware of their infection and susceptible of receiving vaccination N#as = (1-ptas.* tsns_as).*Nas.
where fv is a vector of zeros with one only on the groups currently called for vaccination in a specific moment. N#as refers to untested AS individuals therefore unaware of their infection and susceptible of receiving vaccination N#as = (1-ptas.* tsns_as).*Nas.
In a given population group that no distinction is assumed possible between individuals in the vaccination suitable stages without symptoms. Therefore, in a population group i, the total number of undistinguishable individuals suitable for vaccination (N SVi) is given by Eq. S1.7.d.
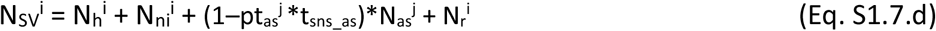
With the above definition, the problem of determining the optimum plan for vaccine application is reduced to the determination, at any given moment in time, of the optimum values of f vi for each population group, until the vaccination campaign is completed.
Dynamic transition equations
The dynamic variation on the number of unvaccinated individuals in each stage over time in vectors of (age-related) population groups is governed by the population balance equations Eqs S1.8.a-g.

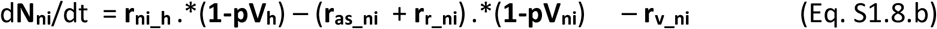
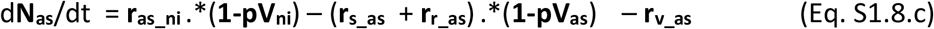
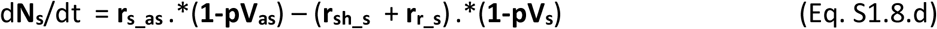
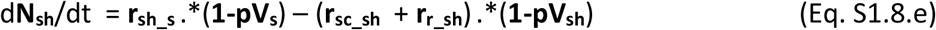

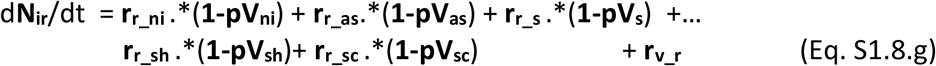
The vaccines once commercialised will likely display a given effectiveness (eV) per population group, which will lead to a proportion of ineffective vaccinations. Those ineffectively vaccinated individuals will not acquire immunity and therefore remain susceptible to infection and to all stages of severity. These must however be accounted for separately as they should not be vaccinated again. The population balances for all vaccinated individuals in their possible stages are presented in Eqs S1.8.h-n.

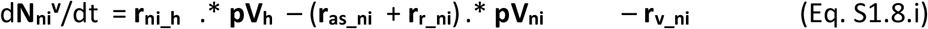
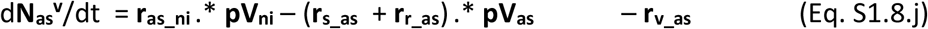
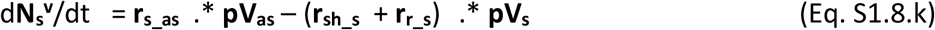
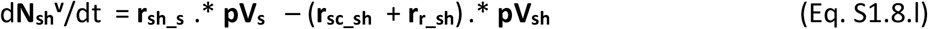
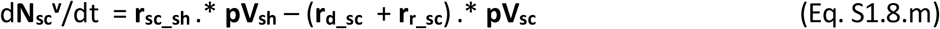
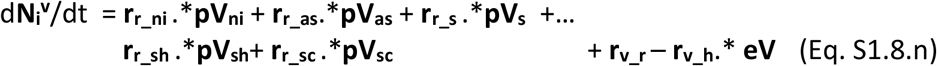
Finally the balance of fatalities is shown in Eq. S1.8.o.
 where pV# is the proportion of individuals in stage # (vector for each population group) that have received a vaccine dose (effective or not).
where pV# is the proportion of individuals in stage # (vector for each population group) that have received a vaccine dose (effective or not).
Source code
The model source code in Matlab® and the Excel files containing all inputs and parameters are available on demand.
Supplementary section II. Computation of the dynamic reproduction number (R)
The reproduction number describes the potential infections of susceptible individuals from infected individuals (33). Since the model generates a deterministic set of values for its outputs at any given time, an instantaneous deterministic computation of the reproduction number (R) is possible. Multiple parameters and variables influence the R such as the duration of the infectious stages; the likelihoods of infection per contact as well as the percentages of individuals transitioning between stages.
The dynamic reproduction number (R) is computed over time according to Eq. S2.1 from the current values of the model state variables. The computation of R assumes that infectious individuals can only infect others while they are in asymptomatic (AS) and symptomatic (S) stages. Although it has been speculated that post-symptomatic recovered individuals may be infectious for some period of time, this has not been considered at this time given the insufficient data. Hospitalised and critical individuals are assumed not able to infect others in the general population as they are in controlled settings. The provided dynamic output of the reproduction number R provides additional information that can be used for decision making.
The computation of the R number is conducted considering that infected individuals can take only three possible infectious paths, namely: (i) Recovery after a period as asymtomatic (AS → R); (ii) Recovery after periods as asymptomatic and symptomatic (AS → S → R) and (iii) Hospitalisation after periods as asymptomatic and symptomatic (AS → S → SH). These paths are made of combinations of four possible infectious stage intervals in which infected individuals spend time and can infect others at their corresponding infection rate (see Table S2.1).
Possible infectious stages intervals for the R number computation.
The dynamic computation of R results from adding the total infection contributions of the four stage intervals as shown in Eq. S2.1.
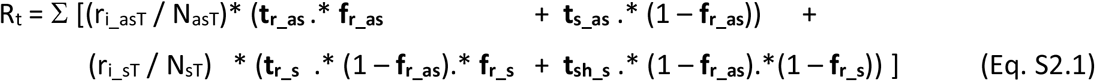 in which, the population group weighted average rates of infection by AS and S are given as per Eqs. S2.2a-b.
in which, the population group weighted average rates of infection by AS and S are given as per Eqs. S2.2a-b.
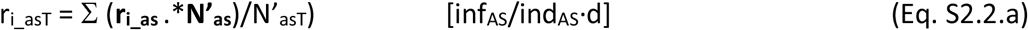
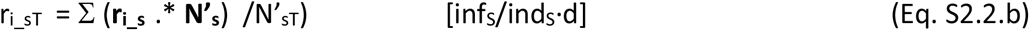 where, N’xj means the sum in stage x of both those unvaccinated and those ineffectively vaccinated (N’X = Nx + Nxv) for all population groups.
where, N’xj means the sum in stage x of both those unvaccinated and those ineffectively vaccinated (N’X = Nx + Nxv) for all population groups.
Supplementary section III. Epidemiological and clinical parameters per age group
Epidemiological and clinical parameters per (age-related) population group used.
Supplementary section IV. Data sources for the epidemiological and clinical parameters
Data sources and level of confidence assigned to the epidemiological and clinical parameters from Table S3.1 for the COVID-19 outbreak case study.
Supplementary section V. Behavioural parameters per age group: COVID-19 case study
Estimated average number of daily interpersonal contacts per individual in each population group (row) with individuals from all the groups (columns) used.
Behavioural and other infectivity relevant parameter as selected for the case study
Estimations of daily contacts per age group used in this work for the case study for Spain compared with those by Mossong et al. (2008) adjusted for average 16.4 contacts per day.
Supplementary section VI. R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation
A strategy based on the estimation the projected avoidable deaths (PAD) by vaccination in each group was developed. The strategy does not require a model to be applied and it establishes the vaccination priority at any given time on the group with the highest PAD by vaccination. The avoided deaths are accounted from two sources and not from the group’s own mortality only, but also from that of those the projected secondary and subsequent infections on the entire population avoided by the vaccination in the group. These are estimated and accounted for using the dynamic reproduction number (R) which can be estimated real time by health system data.
Under the RbPAD strategy, priority is directed at any given moment to the vaccination of the group i with the highest number of projected avoidable deaths per vaccination (see Eq. 1). This is calculated as a function of three elements, namely (i) the risk of infection in that group (as the ratio of the present rate of infections and the number of individuals in the group); (ii) the mortality per infection in the group (fd_nii) (from epidemiological data) and (iii) the mortalities of the projected secondary and subsequent infections avoided that a vaccinated group member would have inflicted on the entire population.
If the R number is used as the estimator of infection propagation at a given moment, the last term of projected secondary infections can be estimated if group-specific detailed information about the ongoing R number is available such that a matrix of R numbers between groups (RM) can be built. This matrix is then projected to any number of infection cycles (n) by powering the matrix to n.
All three terms can in principle be measured or estimated from actual data directly collected by the health systems in a given community. Although the RbPAD strategy is demonstrated below on the dynamic model, its practical implementation does not require or rely on any model, partly decoupling the outcome sequence of priority groups from possible model shortcomings and uncertainties.
The calculation of the projected avoidable deaths for all population groups (PADv), in terms of the model variables, is presented in Eq. 1 (see also Appendix). Eq. 1 was used to evaluate the RbPAD method against the alternatives for the case study example for Spain. A value of three infection cycles for projected propagation (n=3) was used.
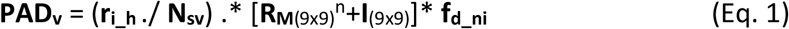 where I(9×9) is the identity matrix of the indicated size to account for each group’s own mortalities.
where I(9×9) is the identity matrix of the indicated size to account for each group’s own mortalities.
The RbPAD methods was applied in conjunction the dynamic model and it is computationally inexpensive as it is evaluated in one single model simulation that follows the defined optimum path. There is no requirement for repeated model simulations to evaluate the objective function for changes in vaccination sequence. The computational low cost allows for its use in conjunction with sensitivity and Monte Carlo simulations to address uncertainty in model parameters. This also allows for the RbPAD method to be deployed together with the model on low cost web-based platforms, making a vaccination optimisation method available globally at no cost.
Supplementary section VII. Comparative evaluation of vaccine distribution strategies under limited logistic rate of vaccination (no shortage of doses)
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluations of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group. Results for vaccine effectiveness values of 100%, 75% and 50% are shwon in Figures S7.1-3, Figures S7.4-6 and Figures S7.7-9 respectively.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Compared vaccination strategies showing active groups called for vaccination, fatalities and R value over time for the case study with data and demographics from Spain. Constant vaccination rate is set at 1% of the total population per day, vaccine effectiveness and population coverage as shown. The best result was obtained after (computationally intensive) evaluation of all possible group sequences (assuming only one single call per group). The computationally inexpensive R-based projected avoidable deaths method is evaluated for weekly cycles and allows for multiple partial calls to any specific group.
Supplementary section VIII. Impact of the behavioural parameters of level of self protection and awareness
Impact of the different levels of self protection and awareness (for those under 65 and for those over 65 years of age) on the number of fatalities that can be avoided if the vaccination is distributed with priority to groups from the highest to the lowest daily interactions vs. from the highest to the lowest mortality. Numbers are for the case study example for Spain presented.
Supplementary section IX. Impact of lpa parameters of R values
For the example case presented above using data from Spain, the estimated behavioural parameters regarding levels of self protection and awareness as shown in Table S5.2 were used. These values were arbitrarily selected and therefore remain of low confidence. An analysis was conducted of their magnitude such that they lead to typical R values observed. See Figure S9.1.
Magnitude estimation of beavioural lpa parameters based on typically observed R values.
Supplementary section X. Sensitivity of the daily number of interactions per group (ni)
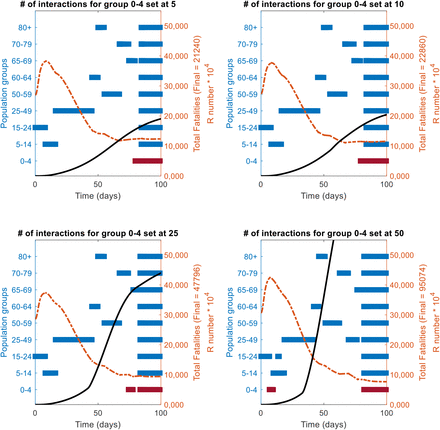
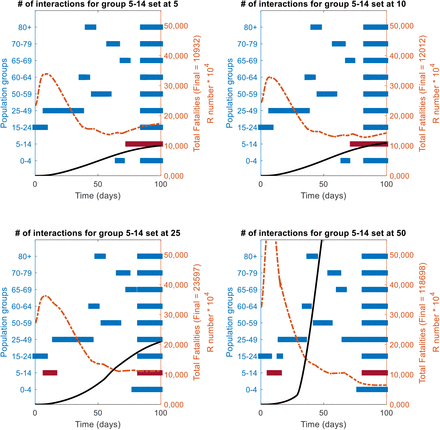
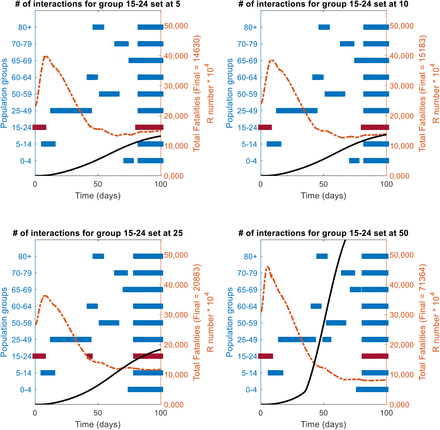
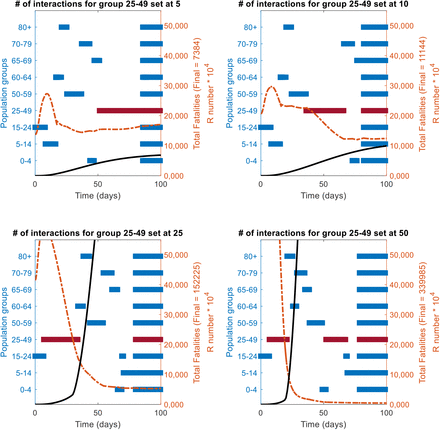
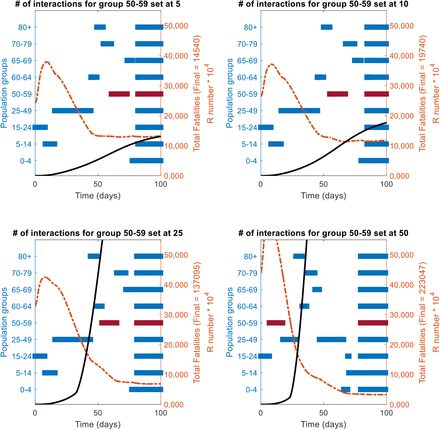
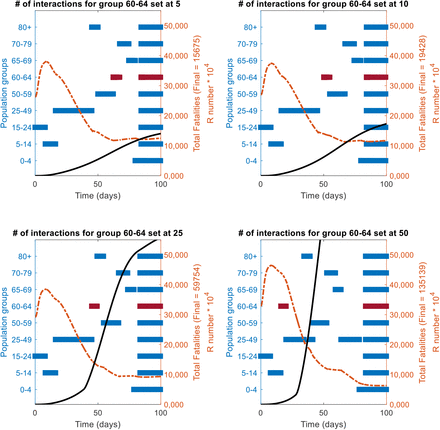
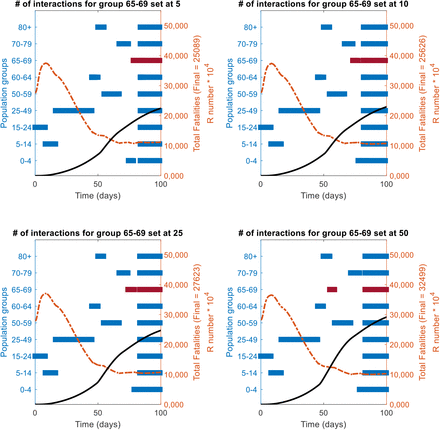
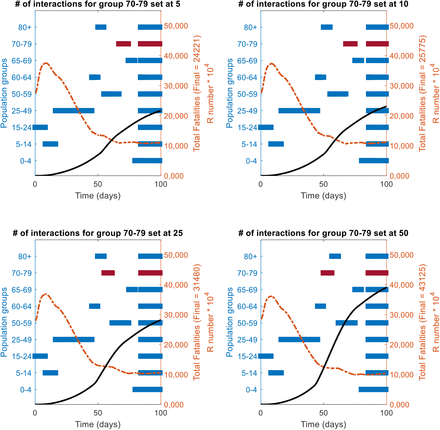
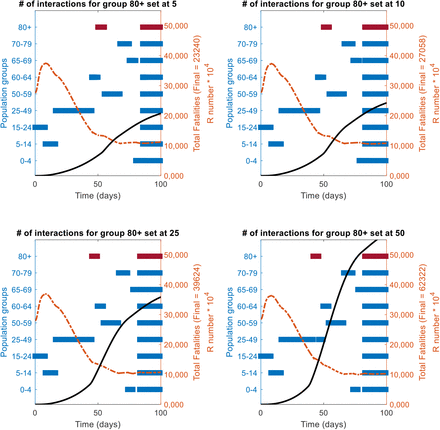
A sensitivity analysis of the changes in the priority position (as per the RbPAD method) funcion of the number of daily interactions/contacts by each population age group is shown. The reference case of vaccine effectiveness of 75% population coverage of 80% is used. The values of 5, 10, 25 and 50 contacts per day were evaluated for each group, while the rest of the groups were kept at their reference state.
In all cases it the more interactions a group has (highlighted in dark red), the further it moves up in priority queu to an early call for vaccination.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Impact of the number of interactions for the group in red bar on their position in the priority queue as per the R-based projected avoidable deaths (RbPAD) method for vaccination prioritisation.
Acknowledgements
Khalifa University (Grant 8474000317 CRPA-2020-SEHA) and the Government of Abu Dhabi for the funding and support provided.
Footnotes
New sections have been added as well as the results for vaccination under scarcity of vaccines.