Abstract
Measures of incidence are essential for investigating etiology. For congenital diseases and disorders of early childhood, birth year cohort prevalence serves the purpose of incidence. There is uncertainty and controversy regarding the birth prevalence trend of childhood disorders such as autism and intellectual disability because changing diagnostic factors can affect the rate and timing of diagnosis and confound the true prevalence trend. The etiology of many developmental disorders is unknown, and it is important to investigate. This paper presents a novel method, Time-to-Event Prevalence Estimation (TTEPE), to accurately estimate the time trend in birth prevalence of childhood disorders correctly adjusted for changing diagnostic factors. There is no known existing method that meets this need. TTEPE is based on established time-to- event (survival) analysis techniques. Input data are rates of initial diagnosis for each birth year cohort by age or, equivalently, diagnostic year. Diagnostic factors form diagnostic pressure, i.e., the probability of diagnosing cases, which is a function of diagnostic year. Changes in diagnostic criteria may also change the effective prevalence at known times. A discrete survival model predicts the rate of initial diagnoses as a function of birth year, diagnostic year, and age. Diagnosable symptoms may develop with age, affecting the age of diagnosis, so TTEPE incorporates eligibility for diagnosis. Parameter estimation forms a non-linear regression using general-purpose optimization software. A simulation study validates the method and shows that it produces accurate estimates of the parameters describing birth prevalence trends and diagnostic pressure trends. The paper states the assumptions underlying the analysis and explores optional additional analyses and potential deviations from assumptions. TTEPE is a robust method for estimating trends in true case birth prevalence controlled for diagnostic factors and changes in diagnostic criteria under certain specified assumptions.
Introduction
In epidemiology, incidence—the rate of new cases—is a fundamentally important metric for estimating causal associations of time-varying risk factors with rates of a disorder [1,2]. Incidence has multiple forms; the most relevant for the present purpose is incidence proportion, which is the proportion of people who develop the disorder (become new cases) during a specified time interval [2]. Incidence is different from prevalence, which is the proportion of a defined population with the disorder at a defined time, typically a calendar year. Prevalence is rarely of direct interest in studying etiology [2]. For some disorders, including congenital diseases and developmental disorders such as autism and intellectual disability, birth year cohort prevalence is used instead of incidence [2,3]. A birth year cohort is the set of all individuals born in a given year. For disorders that are present or predetermined from birth, the time of onset of the disorder is not well defined—it is often before birth—and diagnosis may occur later if at all. Synonyms for birth year cohort prevalence include birth year prevalence, birth cohort prevalence, or birth prevalence. Frequently, articles use “incidence” to mean the occurrence of new diagnoses (incident diagnoses) rather than the occurrence of new cases of the disorder, which are typically unobservable apart from diagnoses. While this usage is understandable because observations inherently represent diagnosis and identification, the difference can be critically important when there is uncertainty about the rate and timing of diagnosing or identifying cases. A case is an individual who has the disorder, regardless of whether they currently exhibit diagnosable symptoms. Serious developmental disorders such as autism and intellectual disability are important topics of study because they cause a significant reduction in quality of life across the lifespan [4] for affected individuals and their families, and they affect large numbers of people.
Studies of time trends in birth year prevalence or incidence are subject to biases resulting from changes in diagnostic factors and diagnostic criteria [2]. Investigators can estimate incidence and birth prevalence directly from data on diagnoses. But concerns that diagnostic factors and diagnostic criteria may have affected the data can lead to a lack of confidence in the validity of direct estimates. Diagnostic factors are those that influence the probability of diagnosing or identifying cases with the specified disorder. Examples include awareness, outreach efforts, screening, diagnostic practice, diagnostic substitution or accretion, waiting times for evaluation, diagnostic criteria, social factors, policies, and financial incentives for diagnosis. Changes in diagnostic criteria can also have the additional effect of changing the effective birth prevalence by including or excluding as cases some portion of the population compared to prior criteria, with the changes occurring when the new criteria take effect.
Consider, for example, this question. If reported birth prevalence increased over time, was this caused by changes in birth prevalence (of cases), the probability of diagnosing cases, diagnostic criteria affecting prevalence, or some combination of these factors? It is challenging to disentangle these effects, and there is no known existing method capable of doing so correctly.
Literature Review
There are many studies on the prevalence of developmental disorders. Yet, very few of them directly address birth year prevalence trends and very few address methods of adjustment for diagnostic factors. The series of reports from the US Centers for Disease Control and Prevention’s (CDC) Autism and Developmental Disabilities Monitoring Network (ADDM) [5-13] estimate the prevalence of autism among children who were eight years old at each even-numbered year 2000 through 2016. Each report describes the prevalence of a single-year birth cohort born eight years before the respective study year. The ADDM prevalence estimates comprise all individuals whom the researchers determined met case criteria, regardless of whether they had been diagnosed. The series of reports represents the trend in birth year prevalence, but the reports describe the findings as simply “prevalence” and do not discuss birth year prevalence or similar names. The ADDM reports suggest that the observed increases in (birth year) prevalence may result from various factors, including changing composition of study sites and geographic coverage, improved awareness, and changes in diagnostic practice and availability of services. However, they do not suggest methods to quantify such effects or to adjust for them. Croen [14] examined birth year prevalence trends in autism and mental retardation in California for birth years 1987 to 1994. They concluded that the data and methods available were insufficient to determine how much of the observed increase reflected an increase in true birth prevalence. Hansen {15} recommends using the cumulative incidence of diagnoses of childhood psychiatric disorders for each 1-year birth cohort as a measure of risk. Cumulative incidence is the sum of new diagnoses, as proportions of the cohort, up to a specified age. It is a measure of diagnoses. Therefore it is expected to be less than the birth year prevalence of cases since, at any given age, there are typically some cases that have not yet been diagnosed. They do not suggest an analytical method to estimate or adjust for the effects of diagnostic factors. Nevison [16] presents California Department of Developmental Services data showing a sharp rise in birth year prevalence of autism over several decades but does not discuss methods to adjust for the effects of diagnostic factors.
Elsabbagh [17] states that investigating time trends in prevalence or incidence requires holding diagnostic factors such as case definition and case ascertainment “under strict control over time” but does not suggest a method for doing so. Campbell {18} reviews prevalence estimates and describes an ongoing controversy about them. They emphasize the distinction between prevalence and incidence but do not mention birth year prevalence. They summarized the CDC ADDM estimates and stated that one cannot infer incidence from the ADDM prevalence estimates. However, they did not mention that the ADDM estimates are birth year prevalence, which serves the purpose of incidence for disorders of early childhood. Campbell indicates that analyses should control for certain diagnostic factors, but they do not suggest a method for doing so. Baxter [4] examined prevalence and incidence but did not mention birth year prevalence and did not indicate whether their use of “incidence” refers to incident diagnoses or incidence of the disorder. Later sections of this paper show why the distinction is crucial. Baxter adjusted for covariates that they assumed introduced bias, including dichotomous variables representing the most recent diagnostic criteria. Such variables inherently represent the time each set of criteria took effect. However, Schisterman [19] shows that controlling for variables on a causal path from the input (time, in this case) to the outcome (prevalence or incident diagnoses) constitutes inappropriate adjustment and biases the estimate of the primary effect (i.e., of time on prevalence or incident diagnoses) towards zero. Similarly, Rothman [2] states that controlling for intermediate variables typically causes a bias towards finding no effect.
For an example of the problem with adjusting for time-varying covariates, consider analyzing a dataset providing observed (diagnosed) prevalence information over a range of years where diagnostic criteria changed at a specific year within that range. An analysis such as one described in Baxter {4} or implied in Elsabbagh [17] might compare prevalence estimates before and after the change in criteria with the goal of correctly adjusting for the effect of the change. Individuals born after or shortly before the change are naturally diagnosed after the change using the revised criteria. In contrast, those born earlier are more likely to be diagnosed using the prior criteria. If there had been no increase in actual birth year prevalence, an increase in diagnosed prevalence would implicate the change in criteria. On the other hand, if there had been an increase in case prevalence with increasing birth year, that would produce an increase in the diagnosed prevalence measured after vs. before the change even if the change in criteria had no effect. The true value of the trend in birth year case prevalence is unknown. This type of analysis is inherently incapable of distinguishing between birth year prevalence trends and changes in criteria or other diagnostic factors. The results could appear to confirm any a priori assumption regarding those trends.
Keyes [20] used age-period-cohort analysis to attempt to disentangle the effects of birth year (cohort) from diagnostic year (period) and concluded that cohort effects best explain observed California data. They also argued that cohort effects represent diagnostic factors, without noting that birth year prevalence is inherently a cohort effect. Spiers [21], in a letter regarding Keyes, pointed out that the method used is extremely sensitive to the constraints specified and could as easily have concluded that period, i.e., diagnostic year, effects best explain the data. Spiers also disputed Keyes’ interpretation of cohort effects. King [22] implicitly used an age-period-cohort analysis, assuming that period effects are dominant and controlling for birth year, thereby minimizing any potential finding of a cohort effect. There is extensive literature on the problems using age-period-cohort analysis to separate the birth year (cohort) effects from diagnostic year (period) effects. The root of the problem is the collinearity, i.e., cohort + age = period, which violates a basic assumption of regression and causes the model to be unidentified. That is, there is a range of possible parameter set values such that estimation could produce any arbitrary one of them. One can constrain the analysis to make it identified; however, the constraint imposes an assumption on the solution. Rodgers [23] states that a constraint of the type used in Keyes “in fact [it] is exquisitely precise and has effects that are multiplied so that even a slight inconsistency between the constraint and reality, or small measurement errors, can have very large effects on estimates.” O’Brien [24], in a book devoted to this topic, states, regarding the relationships of age, period and cohort to the dependent variable, “There is no way to decide except by making an assumption about the relationship between these three variables.” MacInnis [25] showed that the effect of the set of diagnostic factors is represented by the years of first diagnoses, formulates the problem as one of separating birth year from diagnostic year, and shows that age-period-cohort approaches are not suitable for such analyses. In particular, implicit assumptions to make the model estimable cause the resulting estimates to conform to the assumptions, forming circular logic. For example, one can constrain the age term in a regression based on estimates of the age term, as in Keyes [20], but estimating the age term involves making unverifiable assumptions that then appear in the results.
Campbell [18] and McKenzie [26] both point out that various factors could potentially affect the rate of diagnoses without affecting the true case rate.
Schisterman [19] recommends “clearly stating a causal question to be addressed, depicting the possible data generating mechanisms using causal diagrams, and measuring indicated confounders.” This paper directly addresses these issues.
Overview
This work aims to develop and specify a method to estimate birth year trends in case prevalence, correctly adjusted for trends in the set of diagnostic factors and changes in diagnostic criteria. Armed with such a tool, researchers can quantify the effects of the set of variable causal factors separately from the effects of diagnostic factors. Where covariates are available, investigators can estimate associations of birth prevalence with various population characteristics or exposures that may be causal or explanatory.
This paper presents a novel statistical method called time-to-event prevalence estimation (TTEPE). TTEPE solves the problems of prior methods of analysis by utilizing the survival principle. Within each cohort, as cases are diagnosed, fewer cases remain subject to initial diagnosis, which naturally causes a reduction in rates of diagnosis with increasing age. Modeling the age distribution directly rather than using it as a regression term avoids the collinearity problem of age-period-cohort analysis and avoids assuming an age distribution. TTEPE also utilizes the principle that the effect of diagnostic factors presents as diagnoses, such that the year of each initial diagnosis provides important information. TTEPE uses a time-to-event survival method to model the rates of initial diagnoses for all ages and birth cohorts under study. Finding the parameter set that results in the best fit to the observed data estimates the trend in birth year case prevalence adjusted for changes in the set of diagnostic factors and diagnostic criteria. This paper presents the derivation of the analytical method from first principles and states all the underlying assumptions. A simulation study shows that the method effectively separates and quantifies the birth year prevalence trend from the trend in the effects of diagnostic factors, producing accurate estimates.
Method of time-to-event prevalence estimation (TTEPE)
Background
Comparison of prevalence estimates across multiple studies is generally not suitable for informing trends in either birth prevalence or incidence [2]. Different prevalence estimates may use different mixes of birth years and ages, and there are numerous other possible differences between prevalence studies [27]. Many combinations of trends in birth prevalence and diagnostic factors could potentially explain observed prevalence trends. The Literature Review section briefly describes the problems with existing methods, including age-period-cohort analyses and adjusting directly for diagnostic factors and criteria.
Analysis of the cumulative incidence to a consistent age of diagnoses in each birth cohort comes closer to estimating the trend in true birth prevalence, but results are still ambiguous. Some cases may not have been diagnosed by any specified age, and the proportion of cases who were not diagnosed by a specified age may be different for different birth years. Many combinations of trends in birth prevalence and diagnostic factors can produce similar trends in cumulative incidence.
Ambiguity in estimation
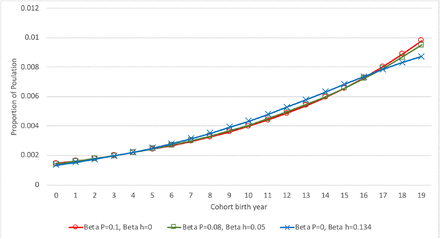
To motivate the development of TTEPE, first consider the ambiguity inherent in analyzing birth prevalence trends using cumulative incidence. How should one interpret a dataset that produces any one of the cumulative incidence curves illustrated in Fig 1; The figure represents synthetic data; some real-world data may be similar. Observed data might produce a curve resembling any one of the curves in the figure. An exponential curve with a coefficient of 0.1 fits all three plotted lines reasonably well. Does this represent a true increase in birth prevalence with a coefficient of 0.1? Does it result from an exponential increase in the effects of diagnostic factors, called diagnostic pressure, with no increase in birth prevalence? Perhaps a combination of both? The three similar cumulative incidence curves represent quite different possible explanations. The information shown in Fig 1 is not sufficient to decide which explanation most closely represents reality.
Example of cumulative incidence under three models. βP is the coefficient for birth prevalence; βH is the coefficient for diagnostic pressure. Red line with circles represents βP = 0.1, βH = 0; green line with squares represents βP = 0.08, βH = 0.05; blue line with crosses represents βP = 0, βH = 0.134.
Fig 1 illustrates a hypothetical example of cumulative incidence of diagnoses to age ten over 20 consecutive cohorts using synthetic data. The legend lists the parameter sets for the three cases. βP is the exponential coefficient of birth year prevalence, and βh is the exponential coefficient of diagnostic pressure by diagnostic year. In the case where βP = 0.1 and βH = 0, birth prevalence increases at e0.1 − 1= 10.5% per year while the diagnostic pressure is constant over time. Where βP = 0 and βH = 0.134, birth prevalence is constant while diagnostic pressure increases e0.134 − 1= 14.3% per year. Where βP = 0.08 and βH= 0.05, birth prevalence increases at 8.3% per year and diagnostic pressure increases at 5.1% per year. The data generating process producing these data uses a survival process as detailed below. An Excel spreadsheet to generate all plots in this paper is available at OSF [28]. The variable h represents diagnostic pressure, the effect of diagnostic factors. The values and trends of cumulative incidence do not provide enough information to discern the relative contributions of the trends in birth prevalence and diagnostic pressure. While the three cumulative incidence curves appear similar, the age distributions of diagnoses are strikingly different for different parameter sets, as Fig 2 illustrates.
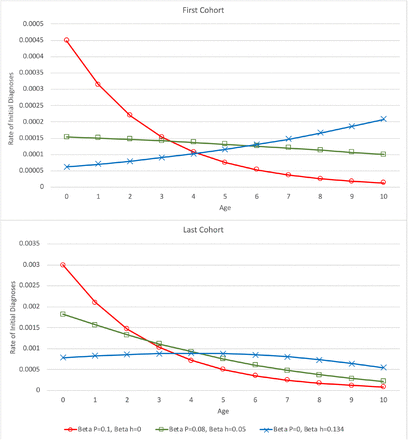
Distribution of diagnoses in the first and last cohorts under three models. βP is the coefficient for birth prevalence; βH is the coefficient for diagnostic pressure. Red lines with circles represent βP = 0.1, βH = 0; green lines with squares represent βP = 0.08, βH = 0.5; blue lines with crosses represent βP = 0, βH = 0.134.
Fig 2 shows the age distributions of diagnoses in the first and last cohorts of Fig 1, with separate plot lines for each of the three parameter sets. In the first cohort (top), the cumulative incidence to age ten is very similar across all three parameter sets, and the same is true for the last cohort (bottom). The growth in cumulative incidence across all cohorts is also very similar for each of the three parameter sets, as shown in Fig 1.
The distinct age distributions associated with different parameter sets are sufficient to ascertain the parameter values specifying the trends in Fig 2. This paper’s remainder explains how modeling the age distribution of first diagnoses enables accurate and unambiguous estimation of the coefficients for birth prevalence and diagnostic pressure.
Significance of birth year and diagnostic year
Diagnostic factors only affect the diagnosis of cases when those cases exhibit diagnosable symptoms, called being eligible for diagnosis. Diagnostic pressure is the probability of diagnosing eligible undiagnosed cases, and it is an effect of the combination of all diagnostic factors. The Introduction lists examples. Diagnostic pressure is equivalent to the hazard h in time-to-event or survival analysis.
For each case of the disorder, the information resulting from diagnostic pressure consists of the time (diagnostic year) of initial diagnosis. Diagnostic pressure has no observable effect before diagnosing each case, and none after the initial diagnosis since TTEPE considers only initial diagnoses. Hence, the effect of diagnostic pressure on the input data is a function of diagnostic year.
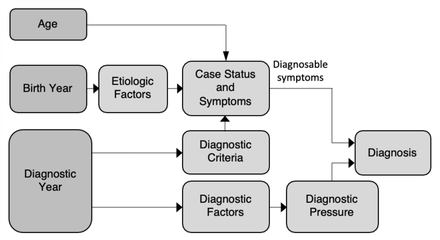
The directed acyclic graph (DAG) in Fig 3 illustrates the causal paths from birth year, diagnostic year, and age at diagnosis. Birth year drives etiologic (causal) factors, which produce the disorder and its symptoms. Symptoms may vary with age. Diagnostic criteria determine whether each individual’s symptoms qualifies them as a case, and criteria may change at specific diagnostic years. Diagnostic year drives diagnostic factors, which form diagnostic pressure. Diagnosable symptoms and diagnostic pressure interact to produce each initial diagnosis.
Directed Acyclic Graph Representing Year of Birth, Diagnostic Year and Age Changes in diagnostic criteria can affect the threshold of symptoms that qualify case status. Criteria changes may change the proportion of the cohort classified as cases, i.e., the effective prevalence.
Development of the TTEPE method
The TTEPE method is based on the DAG of Fig 3 and models the age distribution of initial diagnoses based on the survival principle. The method avoids the identification problem associated with age-period-cohort analysis, and it avoids the problem of inappropriate adjustment for diagnostic factors.
TTEPE is particularly applicable to disorders where case status is established by birth or by a known age, and diagnosable symptoms are present by some consistent age. It is also useful where cases develop diagnosable symptoms gradually over a range of ages.
Data sources suitable for TTEPE analysis provide rates of initial diagnoses by age or, equivalently, diagnostic year for each birth year cohort. The rate is the count of initial diagnoses divided by the cohort’s population at the respective age.
TTEPE is based on these principles: for each birth cohort, the number of cases at risk of initial diagnosis decreases as cases are diagnosed (the survival principle), and diagnostic year is the time when diagnostic factors affect the probability of diagnosing cases exhibiting diagnosable symptoms. TTEPE is an extension of established time-to- event methods. TTEPE simultaneously estimates the birth prevalence and diagnostic pressure functions by fitting a model to the rate of initial diagnoses at each data point. It models the age distribution of initial diagnosis rates via a survival process as a function of birth year, diagnostic year (birth year plus age), and eligibility.
TTEPE introduces the concept of eligibility. A case is eligible for diagnosis if the individual has diagnosable symptoms and not eligible if the individual has not yet developed diagnosable symptoms. For each birth cohort, undiagnosed eligible individuals form the risk set of cases at risk of initial diagnosis. The size of the risk set is denoted R. At each age, there is some probability of diagnosis of each case in the risk set. This probability is the diagnostic pressure (hazard) h. TTEPE uses discrete-time distributions, typically years, so the value of h at each age for each cohort is the number of newly diagnosed cases divided by the size of the risk set; see Kalbfleisch [29]. At each age, newly diagnosed cases are removed from the risk set, and newly eligible cases are added to the risk set. For any given value of h, as R decreases or increases, the rate of initial diagnoses D changes accordingly. This process generates the age distribution. The survival function S refers to cases that “survive” diagnosis at each age. If all cases were eligible from birth, S would equal R. More generally, however, some cases may initially be ineligible and become eligible as they age, so R ≤ S. The prevalence P is the proportion of the cohort that is or will become cases; they may not initially exhibit diagnosable symptoms. The eligibility factor E is the eligible proportion of P; 0 ≤ E ≤ 1.
Unlike TTEPE, in typical survival or time-to-event analysis, including Cox proportional hazards analysis [30], the initial size of the risk set is assumed to have a known value, for instance, an entire population or an entire sample. If the risk set R consisted of the entire population without subtracting diagnosed cases, the estimated hazard function of time  would be equivalent to the population-based rate of diagnoses D at time t. For such methods, if the disorder is rare, it makes little difference whether the risk set is the entire population or the undiagnosed portion.
would be equivalent to the population-based rate of diagnoses D at time t. For such methods, if the disorder is rare, it makes little difference whether the risk set is the entire population or the undiagnosed portion.
Population-based rates of initial diagnoses D are observable while the other variables are not. Values over time of prevalence P and diagnostic pressure h produce values of D as shown in the Illustrative example section. TTEPE extracts the values of P and h from D.
Time-to-event analysis model
The analysis model enables estimation of the temporal trend of birth prevalence P over a range of cohorts, appropriately adjusted for diagnostic pressure h. Both P and h can vary with time. P is a function of birth year, and h is a function of diagnostic year. Estimation of P adjusted for h involves finding the values of the time-based parameters of both P and h that minimize the difference between the TTEPE time-to-event model of D and the observed data while either specifying or estimating the eligibility function E.
Let DBY.A be the population-based rate of incident (first) diagnoses, where BY is birth year and A is age. The model generates predicted values 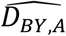 . Modeling proportions rather than counts accommodates changes in each cohort’s population size over time, e.g., due to in- and out-migration and deaths. Alternatively, the analysis could model counts directly. Count values are useful for calculating p-values from chi-square goodness-of-fit measurements.
. Modeling proportions rather than counts accommodates changes in each cohort’s population size over time, e.g., due to in- and out-migration and deaths. Alternatively, the analysis could model counts directly. Count values are useful for calculating p-values from chi-square goodness-of-fit measurements.
Let hDY be the diagnostic pressure at diagnostic year DY. DY = BY + A, subject to rounding, so hDY is equivalent to hBY.A. Let PBY be the case prevalence of birth year cohort BY, i.e., the proportion of the cohort that are cases regardless of how many have been diagnosed. Cases may not initially exhibit diagnosable symptoms, and case prevalence does not depend on eligibility. Let RBY.A be the discrete risk set function of the cohort proportion of eligible cases at risk of initial diagnosis at age A for birth year BY. TTEPE uses R rather than a discrete survival function S to accommodate eligibility changing with age. Let EA be the discrete eligibility function, the proportion of cases that are eligible at age A, bounded by 0 ≤ E ≤ 1. At each age A ≥ 1, P × (EA − EA−1) is the incremental portion of prevalent cases added to R due to increases in eligibility. For simplicity, assume EA increases monotonically, i.e., non-decreasing, meaning that cases do not lose eligibility before diagnosis.
Kalbfleisch [29] gives background on general time-to-event theory and equations.
At each age A for each cohort BY, the rate of incident diagnoses DBY.A = RBY.A * hDY, from the definition of h, above. We write hDY as hBY.A to clarify the effect of A in DY = BY + A.
First, we consider the case where the diagnostic criteria do not change the effective prevalence over the interval of interest. A later section examines the alternative case. Consider three scenarios, differing by the characteristics of EA.
Scenario: constant EA = 1. In this scenario, all cases are eligible from birth, so EA = 1 for all values of A. This scenario is equivalent to standard time-to-event models that do not consider eligibility.
For A ≥ 1, EA − EA − 1 = 0. For the first year of age, A = 0, RBY,0 = PBYE0 = PBY and DBY,0 = RBY,0hBY,0 = PBYhBY,0. In other words, at age 0, all cases are eligible and in the risk set, and the proportion of the cohort that is diagnosed is the proportion that are cases times the probability of being diagnosed.
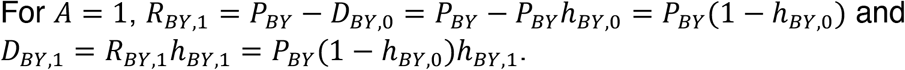 In other words, the size of the risk set decreases from age 0 to age 1 by the proportion of the cohort diagnosed at age 0. The proportion of the population diagnosed at age 1 is the size of the risk set at age 1 times the probability of being diagnosed at age 1.
In other words, the size of the risk set decreases from age 0 to age 1 by the proportion of the cohort diagnosed at age 0. The proportion of the population diagnosed at age 1 is the size of the risk set at age 1 times the probability of being diagnosed at age 1.
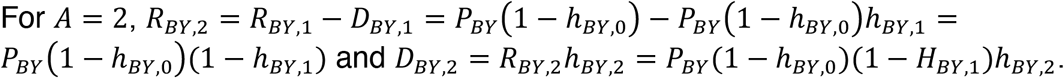 Similarly, for A = 3,
Similarly, for A = 3,
 We can combine these expressions and generalize to, for A ≥ 1,
We can combine these expressions and generalize to, for A ≥ 1,
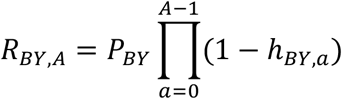 and
and
 In all three scenarios in this paper, the survival function is:
In all three scenarios in this paper, the survival function is:
 The variable SBY.A is the proportion of the cohort BY that are cases that have not been diagnosed by age A. The summation term is the cumulative incidence of initial diagnoses through age A − 1.
The variable SBY.A is the proportion of the cohort BY that are cases that have not been diagnosed by age A. The summation term is the cumulative incidence of initial diagnoses through age A − 1.
Scenario: Increasing EA. E0 < 1 and EA increases monotonically with A. For A = 0, RBY,0 = E0PBY and DBY,0 = E0 PBYhBY,0. For each A ≥ 1, RBY. A = RBY.A−1 − DBY.A−1 + (EA − EA−1) PBY. The incremental increase of EA causes an incremental increase in RBY, A. Then,
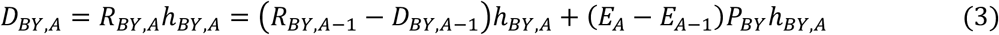 Equation (3) can be used as a procedural definition for software modeling. We can write equivalent expressions for RBY.A and DBY.A as sums of expressions similar to Equation (1), where each summed expression describes the portion of PBY that becomes eligible at each age according to EA. For A ≥ 1,
Equation (3) can be used as a procedural definition for software modeling. We can write equivalent expressions for RBY.A and DBY.A as sums of expressions similar to Equation (1), where each summed expression describes the portion of PBY that becomes eligible at each age according to EA. For A ≥ 1,
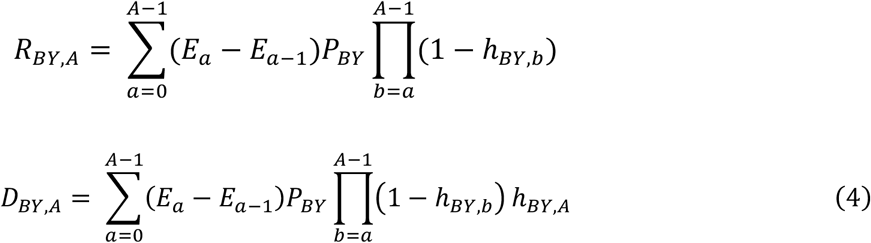 where E−1 is defined to be 0. EA can be defined parametrically or non-parametrically.
where E−1 is defined to be 0. EA can be defined parametrically or non-parametrically.
Scenario: Plateau EA. EA increases from E0 < 1 and plateaus at EA = 1 for A ≥ AE, where AE is the age of complete eligibility, AE < M, and M is the maximum age included in the analysis. Equation (3) applies, noting that for A > AE, (EA − EA −) = 0. Equivalently, combine Equation (2) with the fact that E3 = 1 to obtain  , so
, so
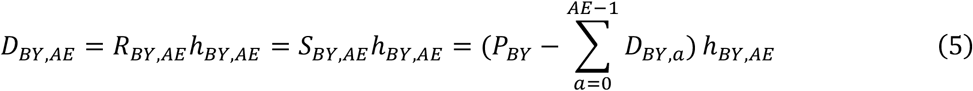 and for A > AE,
and for A > AE,
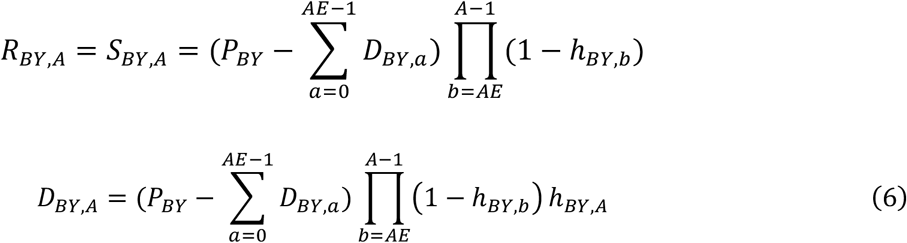 The scenario of increasing EA is a general formulation and may not be needed in typical practice. The plateau EA scenario may be appropriate when external information, such as the disorder’s definition, indicates the value of AE, or when investigators specify AE based on estimates of EA found using Equation (4) or Equation (3). For example, for disorders where by definition, diagnosable symptoms are present by age 3, the plateau EA scenario applies, and the age of eligibility AE = 3. Equations (5) and (6) do not model EA or DBY.A for A < AE. Rather, they use the empirical values of DBY.A for A < AE. In other words, we can estimate the model parameters by modeling the survival function for A ≥ AE and utilizing the observed values DBY.A for A < AE directly in the model.
The scenario of increasing EA is a general formulation and may not be needed in typical practice. The plateau EA scenario may be appropriate when external information, such as the disorder’s definition, indicates the value of AE, or when investigators specify AE based on estimates of EA found using Equation (4) or Equation (3). For example, for disorders where by definition, diagnosable symptoms are present by age 3, the plateau EA scenario applies, and the age of eligibility AE = 3. Equations (5) and (6) do not model EA or DBY.A for A < AE. Rather, they use the empirical values of DBY.A for A < AE. In other words, we can estimate the model parameters by modeling the survival function for A ≥ AE and utilizing the observed values DBY.A for A < AE directly in the model.
Prevalence, cumulative incidence and censoring
The values of P give the case prevalence in each cohort. The cohort prevalence is equivalent to the cumulative incidence of initial diagnoses through the last age of follow-up plus the right-censored portion. This formulation assumes that any difference in competing risks between cases and non-cases in the age range analyzed is small enough to be ignored. This assumption is consistent with Hansen [15]. If the rate of deaths of cases before initial diagnosis exceeds that the cohort’s overall population at the same ages, that excess would constitute a competing risk and reduce the estimated prevalence accordingly.
In all three scenarios of EA, we can express P as a function of S and the cumulative incidence  for A > 0, by rearranging Equation (2) as P = SA + CIA−1. Assuming that eligibility at the last age of follow-up EM = 1, SM = RM. Then, P = RM + CIM−1 and DM = RMhM. The censored proportion is SM+1 = SM − DM, which is equivalent to SM+1 = RM − RMhM = RM(1 − hM). After estimating the model parameters, the estimated censored proportion—the proportion of the cohort that are cases that have not been diagnosed by the last age of follow-up—is
for A > 0, by rearranging Equation (2) as P = SA + CIA−1. Assuming that eligibility at the last age of follow-up EM = 1, SM = RM. Then, P = RM + CIM−1 and DM = RMhM. The censored proportion is SM+1 = SM − DM, which is equivalent to SM+1 = RM − RMhM = RM(1 − hM). After estimating the model parameters, the estimated censored proportion—the proportion of the cohort that are cases that have not been diagnosed by the last age of follow-up—is 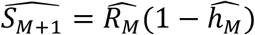 . Diagnoses are counted from the first year of life, so there is no left censoring.
. Diagnoses are counted from the first year of life, so there is no left censoring.
Illustrative example
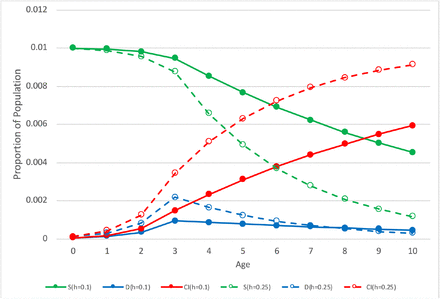
Fig 4 illustrates an example of a single cohort according to the plateau EA scenario showing the relationships between prevalence, diagnosis rates, the survival function, and cumulative incidence CI with two different values of diagnostic pressure h = 0.1 and h = 0.25 and prevalence P = 0.01. In this example, E = 1 for A ≥ AE = 3 and h takes on one of two constant values. The value of h determines the shapes of these functions vs. age. This example shows constant values of h purely for clarity, not as an assumption nor a limitation of TTEPE.
Example of a survival process for two values of diagnostic pressure h. The green lines S denote survival, the blue lines D denote the rate of diagnoses, and the red lines CI denote cumulative incidence. The solid lines represent h=0.1, and the dashed lines represent h=0.25.
As cases are diagnosed, S decreases and CI increases. R is not shown; R = S for A ≥ AE = 3. Only D is observable.
Assumptions
Several baseline assumptions underlie TTEPE analysis. In general, the analytical model’s validity and resulting estimates depend on the validity of the assumptions stated here. If some assumptions are not met, there could be bias in estimation results. Investigators can accommodate deviations from assumptions in many cases. A later section gives approaches to address potential violations of assumptions. The TTEPE method does not assume any particular relationship between parameter values, nor does it require assuming the values of any explicit or implicit variables.
The eligibility function EA under consistent diagnostic criteria is consistent across cohorts.
The diagnostic pressure applies equally to all eligible undiagnosed cases at any given diagnostic year.
The case prevalence under consistent diagnostic criteria within each cohort is constant over the range of ages included in the analysis.
Case status is binary according to the applicable diagnostic criteria.
The discrete-time interval (e.g., one year) is small enough that the error introduced by treating the variable values as constant within each interval is negligible.
No false positives.
Data represent truly initial diagnoses.
Any difference in competing risks between cases and non-cases in the age range analyzed is small enough to be ignored.
The assumption of a consistent eligibility function means that cases develop diagnosable symptoms as a function of age, and the function is the same for all cohorts under consistent diagnostic criteria. In other words, the value of EA at age A is the same for all cohorts BY, while EA varies with A. The section Changes in criteria affecting prevalence discusses a separate effect that might make the eligibility function appear inconsistent even if it is not.
Estimating parameters
TTEPE performs a non-linear regression that estimates the parameters of a model of DBY,A using general-purpose optimization software. The model is based on equations (1) through (6) selected based on the eligibility scenario. The model produces estimates 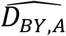 from the parameters and independent variables, and the software finds the parameter values that minimize a cost function cost
from the parameters and independent variables, and the software finds the parameter values that minimize a cost function cost . One suitable implementation of optimization software in the Python language is the curve_fit() function in the SciPy package (scipy.optimize.curve_fit in SciPy v1.5.2). Its cost function is
. One suitable implementation of optimization software in the Python language is the curve_fit() function in the SciPy package (scipy.optimize.curve_fit in SciPy v1.5.2). Its cost function is  , so it minimizes the sum of squared errors. Python software to perform this regression and the simulations described below is available at OSF [28].
, so it minimizes the sum of squared errors. Python software to perform this regression and the simulations described below is available at OSF [28].
Investigators should choose which model equation to use based on knowledge or estimates of the eligibility function EA. The constant EA scenario and Equation (1) assume that all cases are eligible from birth, which may not be valid for some disorders. The validity of the assumption that all cases are eligible by a known age AEA i.e., the plateau EA scenario and Equation (6), may be supported by either external evidence, e.g., the disorder’s definition or estimation of EA The least restrictive approach of the increasing EA scenario uses Equation (3) or Equation (4) to estimate EA Non-parametric estimates  can inform a choice of a parametric form of EA The value of EA at the maximum age studied M should be set to 1 to ensure the model is identifiable. If EA = 1 for all A ≥ AE, that fact and the value of AE should be apparent from estimates
can inform a choice of a parametric form of EA The value of EA at the maximum age studied M should be set to 1 to ensure the model is identifiable. If EA = 1 for all A ≥ AE, that fact and the value of AE should be apparent from estimates 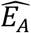 , and the plateau EA scenario applies.
, and the plateau EA scenario applies.
Investigators should choose forms of PBY and hBY.A appropriate to the dataset. Linear, first-order exponential, second-order exponential or non-parametric models may be appropriate. Graphical and numeric model fit combined with degrees of freedom can guide the optimum choice of a well-fitting parsimonious model.
TTEPE preferably estimates P and h simultaneously over a series of cohorts, utilizing data points from all cohorts, thereby enabling well-powered estimation and flexible model specification. Alternatively, it may be possible to estimate h in a single cohort and estimate P based on ĥ under some conditions.
Suppose the population proportion of cases represented in the data is unknown for all cohorts. In that case, estimates of the absolute prevalence, or the intercept, may be underestimated by an unknown scale factor. If that proportion is known for at least one cohort, we can use it to calibrate the intercept. Proportional changes in prevalence between cohorts are unaffected by underestimation of the intercept. If the population proportion of cases included in the sample changes over time, that change reflects changing diagnostic factors, and the estimated parameters of h automatically represent such changes.
Changes in criteria affecting prevalence
Changes in diagnostic criteria could potentially affect rates of initial diagnoses by changing the effective prevalence. This mechanism is distinct from diagnostic pressure. Changes in criteria may change the effective prevalence within a cohort, without affecting symptoms or etiology, by including or excluding as cases some portion of the cohort population compared to prior criteria. A criteria change may change the effective prevalence of the entirety of any birth cohort where the birth year is greater than or equal to the year the change took effect. For birth years before the year of criteria change, a change in criteria that changes the effective prevalence causes an increase or decrease in the size of the risk set R starting at the diagnostic year the change took effect. Generally, diagnostic criteria should be given in published documents, such that changes in criteria correspond to effective dates of new or revised specifications.
Let {CFcy} be the set of criteria factors that induce a multiplicative effect on effective prevalence due to criteria changes that occurred at criteria years {cy} after the first DY included in the study. PBY is the prevalence of cohort BY before the effect of any of {CFcy}. For each cohort BY, the effective prevalence EPBY.A at age A is
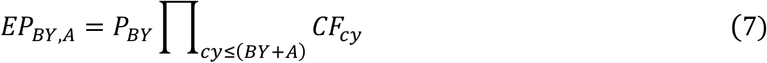 where CF0, the value in effect before the first DY in the study, equals 1. The combination of PBY and the effects of all {CFcy| cy ≤ BY + A} determines the final effective prevalence of each cohort.
where CF0, the value in effect before the first DY in the study, equals 1. The combination of PBY and the effects of all {CFcy| cy ≤ BY + A} determines the final effective prevalence of each cohort.
For a given BY and increasing A, BY + A crossing any cy causes a step-change in the effective prevalence EP. Using a general formulation of eligibility EA per the increasing EA scenario and Equation (3), and for clarity substituting BY + A for DY, we obtain the following. For A = 0, RBY,0 = E0EPBY,0 and DBY,0 = E0EPBY,0h)*,#. For A ≥ 1,
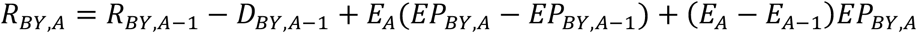 and
and
 The term EPBY.A − EP BY.A.−1 represents the change in the effective prevalence EP when BY + A crosses one of {cy}. As each CFcy takes effect at cy = DY = BY + A, the newly effective CFcy changes EPBY.A and R in all BY cohorts where cy corresponds to an age A in the range of ages studied. These changes in R affect the rates of initial diagnoses D. For cohorts born after cy, CFcy applies to all ages.
The term EPBY.A − EP BY.A.−1 represents the change in the effective prevalence EP when BY + A crosses one of {cy}. As each CFcy takes effect at cy = DY = BY + A, the newly effective CFcy changes EPBY.A and R in all BY cohorts where cy corresponds to an age A in the range of ages studied. These changes in R affect the rates of initial diagnoses D. For cohorts born after cy, CFcy applies to all ages.
The parameters of PBY quantify the birth year prevalence controlled for diagnostic criteria changes, which are represented by {CFcy}. In other words, PBY is the cohort prevalence that would have occurred if the initial criteria had been applied at all diagnostic years included in the study.
To estimate the parameters, use a software model of Equation (8) with optimization software, described in the previous section.
Potential violations of assumptions
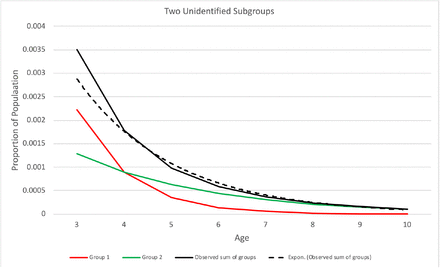
Suppose a dataset represents a non-homogeneous set of cases with different effective values of diagnostic pressure h applying to different unidentified subgroups at the same DY. That would violate the assumption that the diagnostic pressure applies equally to all eligible undiagnosed cases at any given DY. Cases may have differing degrees of symptom severity, and more severe symptoms may result in earlier diagnosis {31], implying greater diagnostic pressure. Fig 5 illustrates this situation. The figure illustrates constant values of h purely for clarity, not as an assumption nor a limitation. If the data represent a combination of unidentified subgroups with differential diagnostic pressure, the distribution of diagnoses is a sum of distributions with different values of h. Such a sum of distributions with different values of h may impair fit with a model that assumes homogeneous h. For data where E = 1 for A ≥ AE (plateau EA), adjusting the assumed value of AE used in estimation, called AE*, may mitigate such errors, as shown in the Simulation study section. Stratified estimation using subgroup data, if available, can avoid the issue of unidentified non-homogenous subgroups. If one suspects non-homogeneity tied to geographic location, such as differences in diagnostic practices or health disparities, stratification by geographic location can elucidate such differences.
Example where observed diagnosis rates represent two unidentified subgroups with different values of diagnostic pressure. The red and green lines represent rates of diagnosis of the two subgroups. Group 1 (red line) has greater diagnostic pressure than group 2 (green line). The solid black line shows the aggregate diagnosis rates. The dotted line shows the exponential fit to the aggregate diagnosis rates. The age of eligibility AE = 3 in this example.
Any imbalance of case prevalence between in-migration and out-migration to and from the region defining the population over the study period would change the prevalence of individual cohorts over time. If some cases of the disorder are caused by exposures after birth, and those exposures vary by year, that would also change the prevalence over time. Either effect would violate the assumption of constant prevalence within each cohort. If time-varying post-natal exposures caused the disorder in multiple birth cohorts simultaneously, they could cause an upward bias in the estimate of diagnostic pressure over the years of this effect.
If some in-migrating cases were diagnosed before in-migration and their subsequent re-diagnoses in the study region were labeled as initial diagnoses, that would violate the assumption of truly first diagnoses. Such an effect would be most evident at greater ages after the diagnosis of most cases. Bounding the maximum age studied M to a modest value, sufficient to capture most initial diagnoses, can minimize any resulting bias.
Apart from subgroups with non-homogeneous h, it is theoretically possible for h to have different effective values for cases of different ages with the same symptom severity at the same DY. Such an effect would represent an age bias in diagnostic pressure, independent of symptom severity. If there is a reason to suspect such an age bias, investigators can add an age term to h in the model and estimate its parameters. One potential form of an age bias in diagnostic pressure h would be age-specific screening for the disorder. Specifically regarding the United States, in 2006, the American Academy of Pediatrics {32} recommended screening tests for developmental disorders be administered at 9-, 18- and 30- (or 24-) month visits. In 2011, Al-Qabandi et al. {33} reviewed the literature on screening and concluded that screening programs were generally ineffective. Screening in the USA starting approximately 2006 might plausibly have increased the effective diagnostic pressure for ages 0 to 2 or 3. An analysis could test for elevated diagnostic pressure at ages 0 through 2 or 3, potentially with this effect starting in diagnostic year 2006. A model could estimate a variable for increased diagnostic pressure at age three across all cohorts or a specified subset. Note that for models that use empirical rates of diagnoses for age 0 through 2 the diagnostic pressure at those ages is not part of the model. An analysis model could also utilize empirical rates at age three. That way, that diagnostic pressure is estimated for ages greater than 3, thereby avoiding any potential bias associated with increased diagnostic pressure specific to age 3.
For datasets where diagnosis follows best practices using gold-standard criteria, the lack of false positives may be a fair assumption. It would be difficult to discover any false positives in that case. Where diagnosis uses a less precise process, some false positives might occur. For example, diagnosticians might produce a positive diagnosis of individuals who do not meet formal diagnostic criteria, perhaps under pressure from the patient or parents, or to facilitate services for the individual. In scenarios where the rate of false positives is significant, the age distribution relative to the rates of true diagnoses may be important. If false positives are uniformly distributed over the age range studied, they would cause a constant additive offset to the rates of diagnoses. True case diagnoses should be more common at younger ages and less common as the risk pool is depleted, so false positives may be relatively more evident at older ages. If false positives are more common at older ages, their effect may be even more obvious.
Model fit
To ensure robust conclusions, investigators should test the model fit to ascertain both model correctness and parameter estimation accuracy. The model fits well if summary measures of the error are small and individual point errors are unsystematic and small {34]. One can examine the fit both graphically and numerically. Plots of DBY. A vs.  at all ages for individual cohorts and separately at single ages across all cohorts can illuminate any issues with fit, which might occur at only some cohorts or ages. Visualization of the model vs. data can expose aspects of the data that might not fit well in a model with few parameters, suggesting a higher-order model or semi-parametric specifications.
at all ages for individual cohorts and separately at single ages across all cohorts can illuminate any issues with fit, which might occur at only some cohorts or ages. Visualization of the model vs. data can expose aspects of the data that might not fit well in a model with few parameters, suggesting a higher-order model or semi-parametric specifications.
Suppose the model uses an assumed age of complete eligibility AE* that differs from the true value of AE represented by the data. In that case, model fit may be impaired, particularly if AE*<AE. As the Simulation study section shows, setting AE*<AE can result in estimation errors. Setting AE* > AE tends not to impair model fit and may improve it in the case of non-homogeneous subgroups; see Fig 5. The presence of non-homogeneous subgroups may be evident from examining model fit.
The chi-square test statistic is a numerical approach to assess absolute model fit. It can be applied to the overall model, individual cohorts, and single ages across cohorts. The p-value associated with the chi-square statistic utilizes observed and expected count values, not proportions. The p-value incorporates the effect of the number of parameters in the model via the degrees of freedom.
Methods that do not model the age of first diagnosis across the range of cohorts and ages can produce unreliable estimates. The Introduction section gives brief explanations of these problems in age-period-cohort analysis and in methods that adjust for variables on the causal path. Models using such methods may fit the data well with some datasets; however, that does not mean that the models can correctly estimate parameters from unrestricted datasets. For example, an age-period-cohort model may implicitly assume an exponentially decreasing age effect and no diagnostic year effect. A dataset may fortuitously happen to conform to that assumption, resulting in excellent model fit. However, using the same model to analyze a dataset that does not follow the assumption may produce substantial errors in both model fit and parameter estimates. In another example, an analysis may test the fit of the model to only a subset or summary of data points, and it may fit the points it tests without recognizing a lack of fit to the remaining points. Simulation studies can detect such problems.
Simulation study
Simulation studies enable researchers to test a statistical method’s behavior where we know the ground truth of all parameters. They use pseudo-random synthetic data generated according to known parameters. A simulation study should exercise the analysis model over a broad range of plausible true parameter parameters. A simulation study can test whether the model and solution method produce accurate estimates of the true parameter values across the full range and detect potential problems such as ambiguity or bias. We tested a model of the TTEPE method via a simulation study, following the recommendations in Morris {35].
The simulation study described here uses a model with first-order exponential forms of birth year prevalence and diagnostic pressure and plateau eligibility with the age of eligibility AE = 3. There are 20 successive cohorts, and the last age of follow-up is M = 10. The parameters of primary interest are the exponential coefficients of birth year prevalence βP and diagnostic pressure βh. The study tested six pairs of values of βh and β P, each ranging from 0 to 0.1 in steps of 0.02, and each pair sums to 0.1. In one parameter set, the prevalence increases as e0.1×BY (10.5% per year) and diagnostic pressure is constant; in another parameter set, the prevalence is constant and diagnostic pressure increases as e0.1×DY (10.5% per year); and the other four parameter sets represent various rates of change of both variables. In all cases, P = 0.01 at the final BY and h = 0.25 at the final DY. These simulations assume the investigators know the correct value of the age of eligibility AE* = 3, following the plateau EA model, from either knowledge of the disorder or estimation of the eligibility function EA The study synthesized each data model in two ways: real-valued proportions without sampling and a Monte Carlo model with binomial random sample generation. The use of real-valued proportions tests the estimation method’s accuracy in the absence of sampling effects in the data. It is logically equivalent to testing in a population of infinite size. Monte Carlo simulation generated data sets using binomial sampling of case counts for each birth cohort and counts of initial diagnoses at each age within each cohort, with 1000 iterations of random data set generation for each set of parameters. The population of each synthetic cohort is a constant of 500,000. The analysis estimated the parameters for each iteration. The results show the parameter estimation bias and model standard error (SE) for each parameter set over all iterations. The study estimated the parameters using the method described above, implemented using the Python SciPy curve_fit() function.
Table 1 shows results using real-valued proportions without sampling, isolating the estimation process from random sampling variations. It shows the bias in estimating each of the four model parameters for each of the six combinations of βh and βP. The biases are minimal and may be caused by finite precision arithmetic in the computer. The greatest bias magnitude in  occurs with βP = 0 and βh = 0.1 and is on the order of 10−10. This result shows that the parameter estimation is extremely accurate in the absence of sampling effects.
occurs with βP = 0 and βh = 0.1 and is on the order of 10−10. This result shows that the parameter estimation is extremely accurate in the absence of sampling effects.
Table 2 shows the Monte Carlo analysis of the same parameter sets where the data use binomial sampling. It shows the bias and model SE of each parameter for each parameter set. The bias of the primary parameter 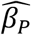 remains small, on the order of 10−5 or 10−6. The SE is relevant when there is sampling, and it shows the effect of sampling compared to Table 1.
remains small, on the order of 10−5 or 10−6. The SE is relevant when there is sampling, and it shows the effect of sampling compared to Table 1.
Table 3 gives results where estimation uses an assumed value of the age of eligibility AE* that, in some cases, does not match the true value of AE = 3 represented by the data. Synthesis uses one homogenous group with consistent h at each value of DY. Estimation used various assumed values of AE* to test the effect of the choice of AE*. Estimation using AE* = 2 results in substantial estimation errors and model misfit that is obvious from plots of data vs. model (not shown). Estimation using AE* = 3, AE* = 4, or AE* = 5 produces accurate results, with slightly more error where AE* = 5. Plots show that the model fits well in all three cases (not shown). The choice of AE* is not critical as long as AE* ≥ AE. These data use real-valued proportions rather than binomial sampling to avoid confusing model mismatch with sampling effects.
Table 4 shows results with an intentional mismatch between estimation assuming one homogeneous group and data representing two unlabeled subgroups with different values of h, illustrated in Fig 5. Note in Fig 5 the visible error of the exponential fit to the data at age = 3 and a good fit for age > 3. In this synthetic dataset, the two subgroups are of equal size, and the true value of h in one group is twice that of the other. This information is unknown to the estimation, and the data does not indicate subgroup size or membership. In the worst case, estimation uses AE* = AE = 3, and the 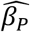 bias is 0.001, which is 1% of the actual value of 0.1. This error is due to the subgroups having different values of diagnostic pressure, and the estimation does not account for that difference. When using AE* = 4 or AE* = 5, the
bias is 0.001, which is 1% of the actual value of 0.1. This error is due to the subgroups having different values of diagnostic pressure, and the estimation does not account for that difference. When using AE* = 4 or AE* = 5, the 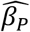 bias becomes 6 × 10.−4 or less, and the model fit is improved (not shown).
bias becomes 6 × 10.−4 or less, and the model fit is improved (not shown).
Discussion
Readers familiar with the problems of methods that assume an age distribution, ignore it, or estimate it inappropriately, including age-period-cohort methods, may be concerned about the possibility that the model may be unidentified or biased. Unidentified means that multiple parameter set values could produce the same predicted values; hence, multiple parameter sets could result from analyzing a single dataset {36]. For example, in age-period-cohort analysis, age, diagnostic year, and birth year interact such that models are inherently unidentified and estimates may be severely biased even if the model fit appears to be excellent with some fortuitous datasets. One can constrain the model to make it identified, but the constraints are inherently arbitrary and can severely bias the results. TTEPE avoids those problems by utilizing the age at first diagnosis data and modeling this information as a non-linear function of birth year and diagnostic year based on first principles, rather than treating it as a separate variable or assuming its value. Fig 2 illustrates why fitting the age distribution of diagnosis enables identifying correct parameter values. As noted in the Introduction, some analytic methods adjust for variables on the causal path, leading to biased estimates. The TTEPE models described here avoid that problem as well.
The simulations described in the previous section show that the simulated model consistently produces correct, accurate estimates of the true parameter values across a broad range of true values. The model is also robust to the small variations in observed values that result naturally from binomial sampling.
It is possible but challenging to prove mathematically that a model is identifiable {36], and we have not done that. We have not found any evidence that the models described are unidentified. The TTEPE method is general; it enables a wide variety of models, with various parametric or non-parametric forms of the variables, and one can add variables. Optimizing parameter values simultaneously across multiple birth cohorts helps discriminate between parameter sets that might interact within one cohort. It is possible to specify a model with collinearity within a single cohort that can result in nonidentifiability in the special case that analysis uses only one cohort. As with any regression, investigators using TTEPE should ensure sufficient data points to precisely estimate all of the specified parameters.
Keep in mind that the eligibility function EA is different from the age distribution of diagnoses; EA is an attribute of the disorder under study. Specifically regarding ASD or autism, the literature shows that cases begin to show predictive symptoms well before age three, and some are diagnosed at age two {37]. According to some but not all diagnostic criteria, symptoms must be present by age three. There is evidence that some cases with milder symptoms who do not meet diagnostic criteria at age three do meet criteria at a later age {38]. Most of those diagnosed at an early age develop more severe symptoms over time {39]. These phenomena are consistent with the discussion above of non-homogeneous subgroups with different effective values of diagnostic pressure. The phenomenon of late development of diagnosable symptoms may be worthwhile to investigate, particularly with datasets representing initial diagnoses over a broad range of ages. That phenomenon can be modeled as the eligibility function continuing to increase for many years of age. There is also evidence that some individuals who meet or appear to meet case criteria before three years of age no longer meet criteria at some later age {40]. As Table 3 and Table 4 show, some errors in estimating the eligibility function and erroneously assuming the homogeneity of the severity of cases have only a minor effect on parameter estimates when the assumed age of eligibility is chosen carefully.
The assumption that case status is binary may not be completely valid, at least in the case of autism or ASD. Different diagnostic assessment tools, assessments by different professionals, and the use of different cut-off thresholds within a tool can produce somewhat different results [37].
This paper states the assumptions that underlie TTEPE analysis. The DAG of Fig 3 illustrates the assumed causal paths from birth year, diagnostic year, and age, including the set of time-varying diagnostic factors and the effect of changes in criteria on effective prevalence. The DAG and associated analysis appear to cover all plausible mechanisms to explain observed trends in rates of initial diagnoses.
TTEPE provides accurate estimates of prevalence parameters with a strong power to detect small differences. The Monte Carlo simulation study in Table 2 shows a magnitude of bias of the prevalence coefficient 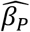 not exceeding 6.5 x 10−5 or 0.0065% per year. The model SE of
not exceeding 6.5 x 10−5 or 0.0065% per year. The model SE of 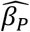 ranges from 0.0012 to 0.0017, where the true βP ranges from 0 to 0.1. Using the largest observed SE and 1.96 x SE as a threshold for 95% confidence intervals, the method can detect differences in βP of 0.0033, i.e., 0.33% per year. Investigators can expect similar performance for real-world datasets that meet the baseline assumptions and have characteristics comparable to the simulated data. The population size and prevalence affect the numbers of incident diagnoses and hence the SE. Note that there are 20 cohorts and 11 ages (0 through 10) in the simulation study, so there are 220 data points. Each data point is an independent binomial random sample. The analysis estimates four parameters that define the curves that fit the data. The large number of independent data points and the small number of model parameters help produce the small bias and model SE. If the each cohort’s population or the prevalence was substantially smaller or the number of parameters was greater, we would expect the bias and SE to be larger. These could occur with small geographic regions, very rare disorders, or higher-order or semi-parametric models, respectively.
ranges from 0.0012 to 0.0017, where the true βP ranges from 0 to 0.1. Using the largest observed SE and 1.96 x SE as a threshold for 95% confidence intervals, the method can detect differences in βP of 0.0033, i.e., 0.33% per year. Investigators can expect similar performance for real-world datasets that meet the baseline assumptions and have characteristics comparable to the simulated data. The population size and prevalence affect the numbers of incident diagnoses and hence the SE. Note that there are 20 cohorts and 11 ages (0 through 10) in the simulation study, so there are 220 data points. Each data point is an independent binomial random sample. The analysis estimates four parameters that define the curves that fit the data. The large number of independent data points and the small number of model parameters help produce the small bias and model SE. If the each cohort’s population or the prevalence was substantially smaller or the number of parameters was greater, we would expect the bias and SE to be larger. These could occur with small geographic regions, very rare disorders, or higher-order or semi-parametric models, respectively.
TTEPE is useful for answering some important questions, such as the actual trend in case prevalence over multiple birth cohorts of disorders such as autism and intellectual disability, as described in Elsabbagh [17] and McKenzie [26], respectively. Accurate trend estimates can inform investigation into etiology. Where datasets include appropriate covariates, stratified analysis can estimate the relationships between various population characteristics and trends in true case prevalence and diagnostic factors. Example covariates include sex, race, ethnicity, socio-economic status, geographic region, parental age, environmental exposure, genetic profile, and other potential factors of interest.
Investigators may utilize domain knowledge to inform specialized analyses. For example, they may incorporate knowledge of mortality rates and standardized mortality ratios, rates of recovery from the condition before diagnosis, or the characteristics of migration in and out of the study region.
It may be feasible to extend TTEPE to disorders and diseases where the time scale starts at some event other than birth. For example, the time origin might be the time of completion of a sufficient cause, and various outcomes may serve as events of interest. It is important to ensure that the eligibility function with respect to the time origin is consistent across cohorts.
Data Availability
Data for this paper are generated by simulation software, which is available at https://doi.org/10.17605/OSF.IO/WPNKU
Acknowledgments
The author thanks Dr. Lu Tian for his expert advice on survival analysis methods; Dr. Lorene Nelson and Dr. Kristin Sainani for guidance on my thesis, which was the genesis of this project and for comments on this paper; Dr. Michael Sigman and Dr. Larry Tang for their thoughtful reviews of the paper; and the Stanford Biomedical Data Science team for their project reviews and insightful comments.
Footnotes
Revised per reviewer comments.