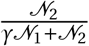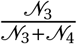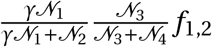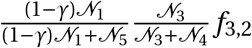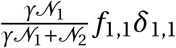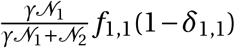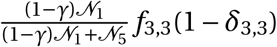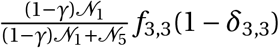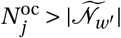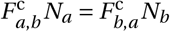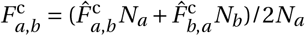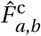Abstract
How effective are ‘lockdown’ measures and other policy interventions to curb the spread of Covid-19 in emerging market cities that are characterized by large heterogeneity and high levels of informality? The most commonly used models to predict the spread of Covid-19 are SEIR models which lack the spatial resolution necessary to answer this question. We develop an agent-based model of social interactions in which the distribution of agents across wards, as well as their travel and interactions are calibrated to real data for Cape Town, South Africa. We characterize the elasticity of various policy interventions including increased likelihood to self-isolate, travel restrictions, assembly bans, and behavioural interventions like washing hands or wearing masks. Even in an informal setting, where agents’ ability to self-isolate is compromised, a lockdown remains an effective intervention. In our model, the lockdown enacted in South Africa reduced expected fatalities in Cape Town by 26% and the expected demand for intensive care beds by 46%. However, our best calibration predicts a substantially higher case load, demand for ICU beds, and expected number of deaths than the current best estimate published for Cape Town.
1 Introduction
The most commonly used Covid-19 models are compartmentalized SEIR (Susceptible, Exposed, Infected, Recovered) models or variations thereof, such as the more realistic SEIICRD model (Susceptible, Exposed, Infected but asymptomatic, Infected and symptomatic, Critical Recovered, Deceased). These models have two decisive disadvantages: They are stochastic ordinary differential equation models of aggregate rather than individual behaviour, and they are driven largely by the value of the reproductive number R0. The high level of aggregation and consequently low spatial resolution of SEIR models make them particularly difficult to apply to emerging market countries which are often characterized by large spatial and socioeconomic heterogeneity. In particular settings with large disparities between neighborhoods within the same city are a challenge for models with low spatial resolution. In few cities is this more prevalent than in Cape Town, South Africa, which has a Gini coefficient of 0.61 Western Cape Govern-ment (2017). The disadvantages of using SEIR models in emerging market cities make it particularly difficult for policy makers to understand the effectiveness of proposed public health interventions such as quarantining infected individuals, travel- and assembly restrictions, as well as behavioural measures like washing hands and wearing a mask.
In this paper, we develop an alternative to the SEIR models: the Spatial Agent-Based Covid-19 Model (SABCoM). Following a bottom-up approach where we start with the interactions of individual agents and study how these affect the disease transmission. We model a set of agents who interact with one another in a network and thereby have a probability of infecting each other. We construct a realistic network of interactions based on the structure of households, agents’ demographics, and their travel patterns across Cape Town. Each agent has an epidemiological state–susceptible, exposed, infected but asymptomatic, infected and symptomatic, critical, recovered, and deceased–akin to the compartments in the SEIICRD model.
We undertake an extensive calibration exercise to calibrate our model to the best available data in order to understand the effectiveness of various policy interventions. On 15 March, President Cyril Ramaphosa declared a National State of Disaster in South Africa, banning all gatherings of more than 100 people.1 Schools and most universities were closed on 18 March. On 23 March, a national ‘lockdown’ was announced by the President to take effect on 26 March, originally to last for 21 days, but ultimately being extended until the end of April. During this lockdown, people were only allowed to leave their homes for access to health services, to collect social grants, attend small funerals, and shop for essential goods. Only workers deemed essential for the Covid-19 response were allowed to leave their homes for other purposes. This was one of the world’s most stringent lockdowns.2 The government adopted a “risk-based approach” and introduced five lockdown levels with the initial lockdown being the most stringent at level 5. Lockdown level 4 was enacted from 1 May and lasted for until the end of May.3 Since then, lockdown level 3 (and later level 3+) is in effect.4 During level 4–and even more so during level 3–more activities were allowed, with the focus shifting from travel and assembly bans to behavioural interventions like wearing masks and washing hands.
First, we are interested in the effectiveness of the stringent lockdown from 26 March until the end of April, in particular in the presence of informal neighborhoods where such measures are likely to be less effective (Adiga et al., 2018; Verma et al., 2018). We find that a lockdown would reduce the expected number of total infections from 3,190,075 to 2,403,360 (−26%) if there are no informal neighborhoods. With realistic values for neighborhood informality, we still estimate an expected number of total infections of 2,542,974, which is still a 20% reduction to the no-intervention baseline. Crucially, the expected number of deaths is reduced by 26% from 44,536 to 33,061 in our most realistic estimation. Similarly, we find a reduction in the demand for intensive care beds by 46% from 14,810 to 7,947 with a peak of infections expected to occur on 31 July 2020.5
One of the main contributions of our paper is that we are able to simulate the progression of the disease across 116 distinct districts, called wards, comprising the Cape Town metro. We find significant variation in the expected percentage of total infections per ward, with a 30.2pp difference between the most and least affected ward. We show that the expected percentage of total infections in a given ward is largely driven by the ward’s population density. However, since more densely populated wards tend to have a younger population, the expected number of deaths is negatively correlated with ward density. We furthermore document substantial differences in the shapes of the infection curves across wards highlighting the importance of our spatial analysis.
Aside from calibration, the biggest challenge we face is model validation. We address this in two ways. First, we compare our no-intervention scenario against a standard SEIICRD model with parameters chosen as closely as possible to our model. We do not expect the two models to align perfectly because of the spatial- and network structure of our model. The expected percentage of the population that becomes infected is 85.3% in our model and 92.5% in the standard (SEI-ICRD) model. The expected time from the beginning of our simulation to the peak is 82 days in our model and 64 days in the standard model and the expected cumulative number of deaths is 44,536 in our model and 37,179 in the standard model. These differences clearly highlight the importance of augmenting the standard model with a bottom-up model. While it will be challenging to differentiate between the two models based on the actual number of infections due to the lack of testing and the large number of unobserved infections, the total number of deaths as well as the timing of the peak of infections are likely to be less biased and thus are suitable differentiators. The second validation we undertake is a comparison to observed infections in Cape Town. For this, we compare the observed number of infections–correcting for the estimated number of unobserved infections–with the model prediction without intervention.6 Our infections for an effective lockdown are well within the lower bound of observed infections and upper bound for a best-estimate of infections.
Furthermore, we do an extensive sensitivity analysis of uncertain parameters. The large number of parameters that are usually required to calibrate an agent-based model generally exceed the available data so that some parameters have to be calibrated manually. In our case these are three policy parameters: the likelihood to self-isolate, a parameter capturing assembly bans, and one parameter capturing behavioural interventions like washing hands or wearing masks. Finally, we test the sensitivity of our model to the virus transmission probability when two individuals interact. Our analysis unveils a range of interesting relationships between parameter values and expected outcomes for total infections, number of deaths, peak infections and the day of the peak infection. Perhaps the most interesting are non-linear relationships, as these indicate particularly sensitive parameter ranges where small changes can have the biggest impact.
We find four such regions. First, the effect of likelihood of self-isolation on total infections is relatively linear. But it has a remarkably bigger effects when it is close to 1.0, i.e. if all patients who test positive are identified through testing and contact tracing and consequently self-isolate. The effect on the expected number of deaths, however, is much more linear. Second, assembly bans are particularly effective at about 20 people, both in terms of curbing the expected total number of infections and deaths. Restrictions stop being effective at more than roughly 50 people. Third, the calibrated value for the effect of policy on the probability of transmission during the lockdown in the presence of informal neighborhoods–interpreted as encouraging the use of sanitizing products and face-masks–is between 0.91 and 0.97 (meaning that the policies reduce transmission by between 9 and 3 percent). In this region, reducing the transmission probability is not particularly effective and a reduction from 0.9 to 0.8 only leads to a reduction in the expected number of total infections from 2,478,549 to 2,302,650, a reduction of 7.1%. By contrast, the same reduction from 0.6 to 0.5 reduces the expected number of total infections from 1,828,698 to 1,365,659, a reduction of 25.3%.
The paper closest to ours is Ferguson et al. (2020), who develop an agent-based Covid-19 model. Different from their model, however, we (i) introduce a travel matrix rather than a simple gravity function to represent travel between districts; (ii) introduce South African contact matrices to reproduce age specific contact patterns; (iii) and introduce informal districts. These additions are important for the Global South context for different reasons. The contact matrices for the global south are distinct from those in the global north, primarily because the elderly in the global south tend to mix more with the young than in the global north. This means that global north models potentially underestimate critical cases and fatalities. The use of informal settlements is important because lockdown policies are known to be less effective in these areas, meaning that global north models will overestimate the effect of these policies. Finally, travel matrices are important because, while informal districts are often far removed from formal districts, contact between these districts is very common for economic reasons.
Other agent-based models of Covid-19 include Tuomisto et al. (2020); Gomez et al. (2020); Chang et al. (2020) and Klôh et al. (2020), but each is lacking one important aspect of our model. Tuomisto et al. (2020), for example do not have informal neighborhoods, as their model focuses on Helsinki. This is also missing in the model of Chang et al. (2020) who focus on Australia. With a focus on Bogota, Colombia, the model of Gomez et al. (2020), is similar to ours in spirit. However, agents in their model do not follow real travel patterns and their infectious disease dynamic does not have an infected-but-asymptomatic state like our model. Transmission from asymptomatic agents, however, has been identified as being a key driver of Covid-19 infectiousness (He et al., 2020). Klôh et al. (2020) use an agent-based model similar to ours to study the disease dynamics in Brazil, also featuring informal neighborhoods. Unlike in our model, however, Klôh et al. (2020) do not explicitly model the travel dynamics of their agents, missing a key transmission vector.
The remainder of this paper is organized as follows. In Section 2, we introduce our main model, including agents, their interactions, and epidemiological status. Section 3 outlines our model calibration and introduces all relevant data sources. In Section 4 we present our main results, including a comparison between the no-intervention and two lockdown scenarios. We also compare our model to a standard SEIICRD model in Section 4.2.1 and undertake a sensitivity analysis of our parameters in Section 4.3. Finally, Section 5 concludes.
2 The Model
We model the spread of Covid-19 in a network of physical interactions modelled as an undirected graph ℊ = (𝒩, ℰ) where the set of nodes 𝒩 represent agents and the set of edges ℰ ⊂ (𝒩 × 𝒩) represent physical interactions between them.7 Our simulation starts with a set of initially infected agents who potentially transmit the disease to their neighbors in ℊ. This network of connections is formed at the start of the simulation, depending on how an agent travels across the city. During the simulation, some connections might become inactive, depending on a policy response, limiting the spread of the virus.
In this section, we discuss: (i) the agents and their characteristics, (ii) the network that governs interactions, (iii) the epidemiological status updates and disease transmission, and (iv) the technical details of how we implement the model.
2.1 Agents
There is a set of agents 𝒩, living in households H in a city with districts W .8 Agents j ∈ 𝒩 are characterized by their epidemiological state Pj and three agent-specific parameters, age aj ∈ A, home district wj ∈ 𝒲, and household number jh ∈ ℋ that remain constant throughout the simulation. We model nine age groups, 𝒮 = {0 − 10, 10 − 20,…, 70 − 80, 80+}, and, in our specific application to the city of Cape Town, 116 districts 𝒲.
An agent’s epidemiological status Pj can take seven values:9 Susceptible to infection (S); Exposed but not infectious (E); Infectious but asymptomatic (I as); Infectious and symptomatic (I s); Critically ill (C); Recovered (R); or Deceased (D). The two sub-categories of the infectious status are important as there are clear indications that some individuals with Covid-19 never show symptoms but still infect others. The critically ill category is used to compare the number who require hospitalization to the critical care capacity of the health system. While such agents are medically still infectious, we assume they are isolated in hospital where they are unable to infect other agents.10
When initialising the agents j ∈ 𝒩, we assign them a district to live in wj proportional to the relative share of agents living in this district. We observe the actual district population and denote it F pop. The proportionality is computed by dividing the population of a district by the total population of Cape Town and then multiplying by the number of agents in our simulation. For each agent j ∈ 𝒩w ⊂ 𝒩, we randomly assign an age group aj using a this probability distribution.
2.2 Agent Interactions
Agents interact in the network ℊ that represents the possible interactions of individuals within a city, calibrated to the available data. The set of agents in district w, denoted 𝒩w, is partitioned into a disjoint set of households ℋw of different sizes. Let 𝒩h,w be the set of agents in household h in district w (i.e. 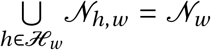 ) with household size Nh,w = |𝒩h,w |. Agents in each household are all connected with one another. The set of households in each district, ℋw, is constructed iteratively, by randomly drawing households sizes Nh,w from the empirical distribution of households sizes specific to each district until
) with household size Nh,w = |𝒩h,w |. Agents in each household are all connected with one another. The set of households in each district, ℋw, is constructed iteratively, by randomly drawing households sizes Nh,w from the empirical distribution of households sizes specific to each district until 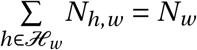 .11 This yields, for each district w, a set of ℋw of different sizes so that there are a total of ℋw = |ℋw | households households in district w.
.11 This yields, for each district w, a set of ℋw of different sizes so that there are a total of ℋw = |ℋw | households households in district w.
Next, we describe how we assign agents to the households so that the modelled household structure is as representative of the empirical pattern of within-household age-dependent contact frequencies as possible.12 Since we iteratively select agents (without replacement) from the set 𝒩w to assign them to households, let  denote the subset of all agents in 𝒩w not selected (and assigned to a household) in any previous step of the algorithm described below.
denote the subset of all agents in 𝒩w not selected (and assigned to a household) in any previous step of the algorithm described below.
First, for each household h in district w, we select a household head as follows: From the set of agents in the ward, we randomly select an agent  (sequentially over households, without replacement) to be head of household h. The selected household head has age-category aj, which was assigned across agents, by district to match available data on age-distributions per district as described in the previous section. This process continues until each of the ℋw households in region w has a household head.
(sequentially over households, without replacement) to be head of household h. The selected household head has age-category aj, which was assigned across agents, by district to match available data on age-distributions per district as described in the previous section. This process continues until each of the ℋw households in region w has a household head.
Second, we add the members of each of the households in district w by the following algorithm. For household h with household head of age ah and household size Nh,w, we select additional household members sequentially, randomly, and without replacement from 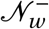 according to the probability distribution constructed from row ah of the empirical contact matrix F hcuntil there are Nh,w members, then move on to the next household.13
according to the probability distribution constructed from row ah of the empirical contact matrix F hcuntil there are Nh,w members, then move on to the next household.13
Non-household interactions take place in the model every day when agents travels across the city. When this happens, agent j in district w belonging to household h forms non-household edges with agents in 𝒩 \𝒩h,w according to an algorithm that represents the best estimates from two empirical data files: (i) The non-household contact matrix F oc;14 and (ii) The travel matrix Ftv which records the probability that an agent in district w travels to district w′ on any given day.15 The number of non-household connections that agent j makes, 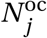 is the total number of average non-household contacts for an agent in age category aj as recorded in F oc.
is the total number of average non-household contacts for an agent in age category aj as recorded in F oc.
The set of agents with whom agent j forms non-household edges is constructed in two steps. First, agent j selects a destination district w according to the probabilities in F tv. Iterating over all agents, this yields a new effective population of each district that consists of the agents whose home district it is, as well as all agents from other districts who selected it as a destination.16 Denote the effective population of district w′ as 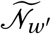 . Second, for each agent j with destination district w, we create edges to agents that are randomly selected from
. Second, for each agent j with destination district w, we create edges to agents that are randomly selected from 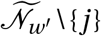 , without replacement, according to the probability distribution implied by the non-household contact matrix F oc, until
, without replacement, according to the probability distribution implied by the non-household contact matrix F oc, until 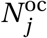 new edges have been created.17
new edges have been created.17
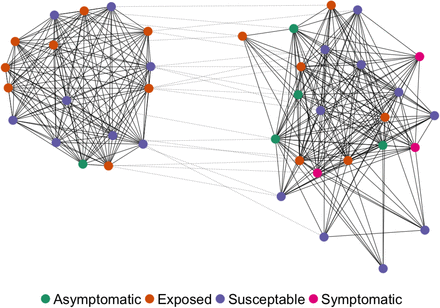
To give an impression of what ℊ might look like after the algorithms above were applied, Figure 1 present a stylized network for a model with 40 agents in 2 districts.
City network example.
This schematic shows a 40 agent, 2 district city network at t = 14 generated by our algorithm. Household edges are dotted and other edges are continuous. The nodes are agents and the colours mark differences in their epidemiological status pj. The main clusters that can be observed represent agents that travel to the same location every day. The virus can then spread to other districts via the household links when agents travel back to their home district.
2.3 Epidemiological Status Updates and Disease Transmission
As time progresses, agents will update their epidemiological status P. Disease transmission will take place as agents interact. interactions are contacts between two agents who share an edge in ℰ. When agents i and j interact, virus transmission occurs with probability π(Pi, Xi ; Pj, X j). The first agents to update their epidemiological status from susceptible S to exposed E are a set 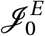 of agents that is created at the start of the simulation. To determine which agents are exposed, we use F ca, a list that contains the total number of cases per district. For each initial case in F ca, we first select a district using a probability distribution obtained by using minmax normalisation on F ca. Within this district, we pick an agent j using a random uniform distribution and update its status to Pj = E, and assume that the agent has been in this for a random number of days between 0 and τE, where τE is the latency period.
of agents that is created at the start of the simulation. To determine which agents are exposed, we use F ca, a list that contains the total number of cases per district. For each initial case in F ca, we first select a district using a probability distribution obtained by using minmax normalisation on F ca. Within this district, we pick an agent j using a random uniform distribution and update its status to Pj = E, and assume that the agent has been in this for a random number of days between 0 and τE, where τE is the latency period.
The progression of the disease for all agents j ∈ 𝒩, where Pj ∈ {E, I as, I s,C, R} is modelled as follows. An agent j in age category a, whose status is Pj = E will transition to infectious and symptomatic (I s) with probability πs or to infectious but asymptomatic (I as) with probability πas = (1 − πs), after the latency period of τE days. An agent with Pj = I as, will recover after τas days and update its status to the recovered status, Pj = R. If the agent is symptomatic with Pj = I s, then after τs days the agent either enters the critically ill status Pj = C with age-dependent probability πC,s or will recovers with probability (1 − πC,s). If an agent has status Pj = C, we assume that the agent requires hospitalization and there is a probability of dying. After τC days, an agent with Pj = C enters the deceased status, D, with age-dependent probability δLπD,s or recovers with probability (1 −δLπD,s), where πD,s is based on clinical data and δL is a multiplier that is based on the empirically observed increased chance of death when the health system is overburdened:
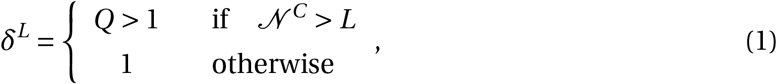 where L is the capacity of the health system, 𝒩 C is the total number of agents in the critical state, and Q is the empirical multiplier when hospital capacity is overwhelmed.
where L is the capacity of the health system, 𝒩 C is the total number of agents in the critical state, and Q is the empirical multiplier when hospital capacity is overwhelmed.
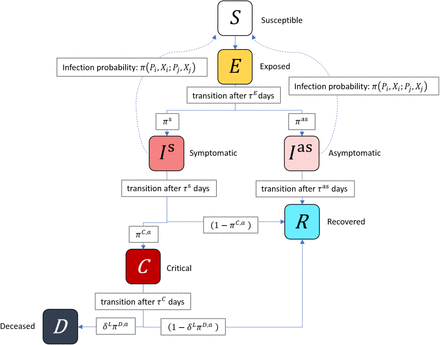
Figure 2 presents the disease progression schematically.
Schematic of the disease progression.
This schematic shows the disease progression modelled in SABCoM. Solid arrow between compartments represent transitions of an agent to different disease statuses. Dashed arrows represent social connections along which the virus may be transmitted from infectious to susceptible individuals.
After all statuses have been updated, virus transmission to agents with Pj = S will take place between agents that have an edge in network ℊ. Infections spread from the infecting agent with status Pj ∈ {I as, I s}.
For every agent with Pj = I s there is a probability of 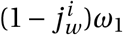 , where ω1 is the likelihood that an agent with symptoms is aware of her status (and then self-isolates). The relative informality level of the infectious agent’s home district (relative to the most formal district) is denoted
, where ω1 is the likelihood that an agent with symptoms is aware of her status (and then self-isolates). The relative informality level of the infectious agent’s home district (relative to the most formal district) is denoted 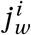 and is obtained from the observed level of informality per district F in, that an agent will reduce her interactions to household members only.18 Introducing this behavioural heuristic is not possible in the standard epidemiological literature and an important contribution of our paper.
and is obtained from the observed level of informality per district F in, that an agent will reduce her interactions to household members only.18 Introducing this behavioural heuristic is not possible in the standard epidemiological literature and an important contribution of our paper.
Next, all agents will reduce their edges based on policy restrictions that are currently in place:
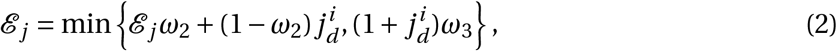 where ℰ j is the set of edges involving agent j, ω2 represents the fraction of travel network connections that are active for each agent, and ω3 is the maximum number of non-household contacts any agent is allowed to have each day.
where ℰ j is the set of edges involving agent j, ω2 represents the fraction of travel network connections that are active for each agent, and ω3 is the maximum number of non-household contacts any agent is allowed to have each day.
Having updated her edges, the infecting agent will interact with all agents 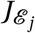 with whom she is still connected. For each agent
with whom she is still connected. For each agent 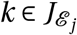 (located in ward w), the effective probability πE that she will transmit the disease to a neighbour with Pj = S is:
(located in ward w), the effective probability πE that she will transmit the disease to a neighbour with Pj = S is:
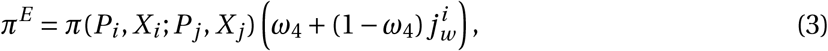 where π(Pi, Xi ; Pj, X j) is the base probability of infecting another agent, ω4 is a policy multiplier that can decrease the probability of infection. As
where π(Pi, Xi ; Pj, X j) is the base probability of infecting another agent, ω4 is a policy multiplier that can decrease the probability of infection. As 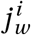 increases from 0 (fully formal) to 1 (fully informal), the effectiveness of policies represented by ω4 falls from fully effective to zero. In the model, π(Pi, Xi ; Pj, X j) is the main parameter that drives the spread of the virus. It is comparable to the parameter β that governs the rate of transmission in differential equation compartmental models (see the model in Appendix C).
increases from 0 (fully formal) to 1 (fully informal), the effectiveness of policies represented by ω4 falls from fully effective to zero. In the model, π(Pi, Xi ; Pj, X j) is the main parameter that drives the spread of the virus. It is comparable to the parameter β that governs the rate of transmission in differential equation compartmental models (see the model in Appendix C).
2.4 Implementation
The model is implemented in Python and the code is publicly available.19 During our simulation we store the agent variables and parameters in memory. We make use of auxiliary variables to keep track of how long each agent has been in each epidemiological state. Furthermore, we keep track of the number of other agents have been infected by each agent in the current period as well as in total. Finally, we store the neighbours each agent has, their number of contacts as well as the household number that they belong to.
For our first simulation day, we record the set of edges ℰ. At every simulated day t, we record the epidemiological status P, wj district number, and aj group of every agent along with the number of other agents it has infected during that day. This data is then either stored in .csv or .graphml files.
The model dynamics are explored through Monte Carlo simulations. This means that we simulate the model M times. For each simulation, we seed the pseudo random number generator with a different number m ∈ M, ensuring both that its results can be replicated and that changes in output for the same seed can be attributed to changes in policy rather than changes in stochastic factors.
3 Calibration
Our model calibration can be divided into four parts. First, we set a baseline for the simulation-specific parameters. Second, we assign values to parameters that are associated with the clinical features of Covid-19 progression. Third, we calibrate the geo-spatial and demographic features to data for the City of Cape Town (as an example of the type of metropolitan area typical of the Global South). Finally, we assign baseline values to the policy parameters based on South African and global data.
Overall, there are 14 parameters and 9 input files that control the numerical simulation. Of the parameters, 3 are simulation parameters, 9 are related to the Covid-19 pathogen (Table 1), 1 that considers the capacity of the health system in Cape Town, and 4 are policy parameters.
Covid-19 pathogen related parameters and age-specific probabilities
3.1 Simulation Parameters
We run our simulations with 𝒩 = 100, 000 agents. Every simulation runs for a minimum of T = 350 days and is repeated M = 50 times to average out stochastic effects. Because we simulate each parameter set M = 50 times, we are able to produce confidence intervals for our predictions.
3.2 Covid-19 Parameters
With respect to parameters which pertain to the Covid-19 pathogen, we choose best available estimates from peer-reviewed medical journals. Despite there still being considerable uncertainty around the clinical course and transmission of the disease, we were able to find literature estimates for most parameters.
The Covid-19 parameters are chosen from recent studies (see Chen et al., 2020; Verity et al., 2020; Huang et al., 2020, among others). Table 1 provides an overview of all parameters and their sources.
Because we could not find a literature estimate for π(Pi, Xi ; Pj, X j), the probability of transmission when an infectious agents comes into contact with a susceptible agent, we will set it together with our policy parameters so that our infection curve is representative for what has been observed in the City of Cape Town.
3.3 Applying the Model to the City of Cape Town
We calibrate our model to the metropolitan municipality of Cape Town, which covers over 2,400 square kilometers with a population 3, 740, 026 as of 2011.20 The city is sub-divided in W = 116 administrative districts, known as wards21. Calibrating our model to Cape Town means that we populate our input files with data that is representative of the Cape Town metropolitan area and set our health system parameter based on hospital capacity in Cape Town.
Our first input data file F popcontains the population and age distribution per ward, the second input file F inis a measure of the share of the ward which is classified as informal. The third file F hsis the empirically observed household size distribution for all districts in the city. For each of these files, we use ward level data from the South African National Census for 2011, provided by Statistics South Africa.
Then, we make use of social contact matrices for South Africa as a proxy for social contact matrices in Cape Town, obtained from Prem, Cook and Jit (2017). The contact matrices are the A× A age-group household contact matrix F hc, and non-household contact matrix F oc, respectively. These matrices specify how many average daily contacts people in a particular age group have with others, by age group. The matrices include total contacts, household contacts, as well as work and school contacts. Since we only consider household and non-household contacts, their reported household contacts form F hc. To obtain a measure for non-household contacts, F oc, we simply subtract household contacts, F hc from total contacts. We illustrate the total household and non-household social contact matrix in Table 2. Between the age groups 0-10 and 40-50 we see a significant share of interactions occur on the diagonal, indicating predominantly within age-group contacts. However once one moves into age groups 50 - 60 and above, the diagonals become less significant, indicating substantial cross-age group interaction. This is a particularly important feature given mortality rates are highest among the elderly, who also have the highest cross-age group interactions, especially with the young.
Age-based social contact matrix
This table shows the age-based social contact matrix of total contacts for South Africa obtained from Prem, Cook and Jit (2017). In this representation, we normalize contacts row-wise within age group so each value can be interpreted as a percentage of all contacts for that specific age-group. Values should be read across columns with each column representing the person from which the contact originates and each row representing the person receiving the contact. We add one additional column and row to this table corresponding to individuals older than 80 years old. While our model contains individuals in this age group, the data we use does not include this age group. We set the contact matrix values of individuals above the age of 80 equal to the contact matrix values of individuals between 70 and 80 and therefore explicitly assume an identical contact structure.
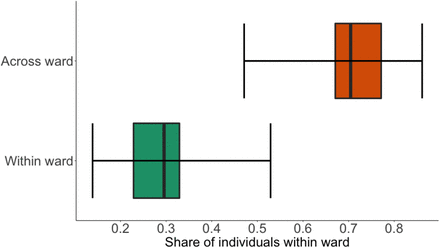
Next, we construct a travel matrix F tvfor Cape Town using travel patterns from the 2013 National Household Travel Survey, undertaken by Statistics South Africa, a nationally representative travel survey. We use these data to calculate a travel matrix which contains the probability of travel across all pairs of wards in our model, as well as the probability that an agent does not travel across wards (an example being an agent who lives and works in the same ward).22 We describe the process by which we map the travel survey data to our model in more detail in Appendix B. In Figure 3 we show the distribution of the share of individuals within each ward that travel to a different ward for work and school and those individuals who reside and work or attend school in the same ward. The mean share of individuals within wards who reside, work, and attend school in the same ward is 28% while the mean share of individuals within wards who reside in one ward but travel to another ward for work and attend school is 72%. As a result, there is substantial cross-ward travel on average, but in some wards within ward travel is sizeable - for example, in the ward with the highest share of within ward travelling individuals, this share accounts for 52.9%. However, as a single destination, the share of individuals who live and work or attend school in the same ward is the highest. Put differently, while most people within a ward travel outside of that ward for work and school, this represents travel to all other 115 wards apart from the one the person lives in. However, when we look at the most travelled to ward across all possible wards, this is almost always the ward where the individual lives.
Within and across ward travel patterns
This figure a box plot of the distribution of travel patterns for individuals across wards. We split households into two groups (i) Across ward travelling individuals, who represent individuals who reside in a given ward and travel to a different ward for work or school and (ii) Within ward travelling individuals, who represent individuals who reside and attend work or school in the same ward.
For infection data, we make use of F ca, a data set that contains the total number of cases per ward in Cape Town. There were 310 detected infections in Cape Town on the 29th of March 2020.23 We divide this number by 37.4 to reflect that we use 100,000 agents to represent a city of about 3,740,000 people. However, since there were many undetected cases we make the assumption 86% of cases remained undetected, based on the findings of Li et al. (2020) who estimated this to be the case for China before the lockdown. Thus, we initialise our simulation with 59 infected agents. We distribute these agents over the wards based on a probability calculated by normalizing the amount of observed infections per ward.
Finally, we calibrate the health system capacity as follows. According to official sources, there were 2162 acute beds in the Western Cape province on the 22nd of May 2020.24 Additional 1428 care beds were scheduled to be provided by temporary hospitals. Of these, 89% will be in Cape Town. Assuming that this ratio holds for all beds, we set our health systems capacity to be L = 0.000917, the fraction of acute beds available in Cape Town divided by the total population.
3.4 Assigning policy parameters
Our policy parameters are based on South African lockdown policy. We use the Stringency Index F str in (Hale et al., 2020), published by the Oxford Blavatnik School of government, to track how strict South African regulations are over time. The index scores lockdowns worldwide on a 0-100 scale where 0 is the least and 100 is the most stringent lockdown. In response to the Covid-19 outbreak, South Africa went into a 87.96 stringency index lockdown that at midnight on 26 March 2020. The stringency of this lockdown was eased to 84.26 on the first of May, to 80.56 on the first of June, and then to 76.85 on June 8th.
The lockdown policy measures included various measures that are meant to delay the spread of the virus. These policies affect different aspects of the model via the likelihood to self-isolate ω1, travel restrictions ω2, assembly bans ω3, and behavioral interventions like washing hands and wearing masks which reduce the probability of infection ω4. The values of these parameters changes over time and have been calibrated as follows.
While data for these parameters is generally very difficult to obtain, we were able to find useful information for ω2. For this, we base the effect that the lockdown has on contact frequency on the change in traffic in Cape Town. We obtain this data from the Google Mobility Reports F goo.25 Here, we have selected mobility data for the Western Cape, South Africa from the 29th of March 2020 till the 14th of June 2020. During this period, in which lockdown policies were in place, travel was on average 54% of the median value for the corresponding day of the week during the five week period from January the third till February the 6th in 2020. For the first 78 days of our simulation, we set ω2 equal to its equivalent value in the Google Mobility Report. After that, we assume that relative mobility remains equal to the last observed value. While we are aware that seasonality might influence these numbers, the Google data currently represent the best available data.
For the other (uncertain) parameters, we hand-picked initial values along with the probability of transmission so that the model produced infection rates that are in line with what we have observed over the period for which there was Google travel data. We set to 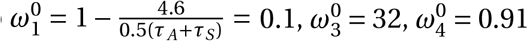 , and the probability of transmission π(Pi, Xi ; Pj, X j) = 0.006.
, and the probability of transmission π(Pi, Xi ; Pj, X j) = 0.006.
For the rest of the simulation, the value of the uncertain policy parameters evolves with changes in the relative stringency of South African lockdown policies F str in. Thus for each point in time during the first 78 days of the simulation, we set 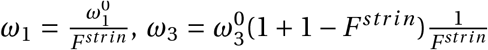 , and
, and 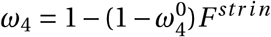 . After the period for which we have observed data, we again assume that the last policy variable is extended for the rest of the simulation.
. After the period for which we have observed data, we again assume that the last policy variable is extended for the rest of the simulation.
As described in section 2.3, the level of informality affects these policy parameters. Table 3 provides an example of how the policy parameters might change depending on the level of informality of a ward.
The effect of informality on policy parameters
This table shows the effective policy parameters for a completely formal ward as well as the most informal ward in Cape Town (i = 0.66). The data on informality is taken from the 2011 South African National Census conducted by Statistics South Africa. The calculations to arrive at the effective policy parameters for the most informal ward are derived from the equations presented in section 2.3 and are: ω1 = 0.1×0.66, ω2 = 1−((1−0.54)×(1−0.66)), ω3 = 32×(1+0.66), and ω4 = 1 − (1 − 0.91) × 0.66.
4 Results
Our model is calibrated to be a realistic representation of the economic, behavioural, and geo-spatial structure of the Cape Town City area. Throughout this section, we present results for simulations with our calibrated model over multiple random seeds, take the average effects, and report these along with maximum and minimum values across the seeds.26 For each scenario, we also report the basic reproductive number R0 which we have calculated as how many agents the first infected agent ended up infecting. Because R0 depends heavily on which agent is first infected, sampled the 300 agents using Latin Hypercube sampling (Stein, 1987) and re-port summary statistics for the R0 rather than just one number.
4.1 Scenarios
For our results, we consider three scenarios. The scenario of primary interest is one in which all of our parameters are are equal to those described in Section 3.4. We shall refer to this scenario
as the “ineffective lockdown” because it is characterized by a lockdown and because this lock-down is assumed to be less effective in districts that have informal components. To explore the influence of these two key aspects, we contrast this scenario to one in which the lockdown is equally effective in all scenarios, this is “the lockdown scenario,” and one in which we assume no interventions by the government, “the no-intervention scenario,” in which ω1 = 0, ω2 = 1, ω3 = ∞, and ω4 = 1.
4.1.1 No intervention
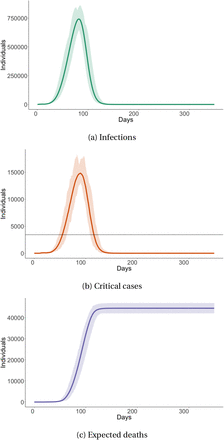
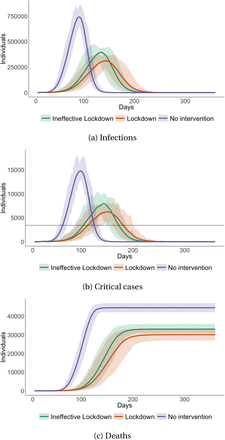
We first explore the no-intervention scenario to better understand the dynamics of the virus if left unchecked. This allows us to then clearly illustrate the mechanisms by which the two types of lockdown reduce infections later in this section. Figure 4 shows aggregate results for infections, critical cases, and expected deaths from the no-intervention scenario. Infections peak at 741,273 cases on simulation day 82 (June 19th) and by the end of the simulation (after one year), 3.19 million people, or 85.3% of the population, have been infected. In this scenario the average R0 is 3.78 and its standard deviation is 2.54.
No-intervention scenario aggregate infections, critical cases and expected deaths
This figure shows simulated (i) infections, (ii) critical cases, and (iii) expected deaths from our no-intervention scenario. The line shows mean effects from a simulation of 100,000 agents across 50 random seeds. Error bands show the maximum (worst-case) and minimum (best-case) values across 50 seeds. We scale the y-axis to the Cape Town population. In sub-figure (b), we include a horizontal line indicating the hospital bed capacity of 3,433 beds.
A few features are worth noting. First, while there is some variation across seeds, the level of infections in the best and worst scenarios are broadly consistent with the mean number of infections across seeds. Second, critical cases peak at 14,810 cases on day 89 (26th of June), but the hospital system already becomes overburdened by day 55 (May 23rd) and this lasts until day 115 (July 22nd), as critical cases exceed the hospital bed capacity as indicated by the horizontal line. This overburdening leads to excess deaths through the multiplier δL in our model which increases the probability of death once the health system becomes overburdened. Lastly, our model predicts that in the no-intervention scenario the virus results in over 44,536 expected deaths in Cape Town and a case fatality rate of 1.40%. As with infections and critical cases, the level of deaths in the best and worst case scenario’s are broadly consistent with the mean number of deaths across seeds.
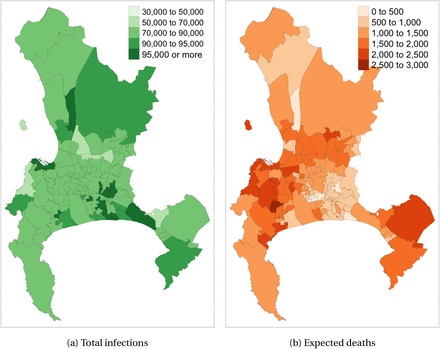
In addition to aggregate statistics, a key feature of our model is the ability to study the spread and incidence of the disease spatially. In Figure 5, we show total infections and total expected deaths as they are distributed across different wards in Cape Town, per 100,000 individuals. There is strong spatial variation in both infections and expected deaths with certain hot-spots appearing. This alone highlights the need for spatial models–disease incidence is heterogeneous across space. The district level variation in infections is substantial. While 85.3% of the total population become infected, in some districts, more than 95% of the population end up infected, while in another district only 64.8% of the population become infected. There is also strong variation in the number of expected deaths with the worst affected ward being expected to see 2.6% of the ward population dying, while the least affected ward is only expected to see 0.32% of the ward level population dying. Finally, there is also sizeable variation in the case fatality rate, with some areas having a high number of expected deaths relative to infections.
No-intervention scenario Covid-19 infections and expected deaths across wards
This figure shows the number of total infections and total expected deaths within a ward from our no-intervention scenario on a map of Cape Town. We scale the legend to show numbers per 100,000 individuals. These results show mean effects from a simulation of 100,000 agents across 21 random seeds.
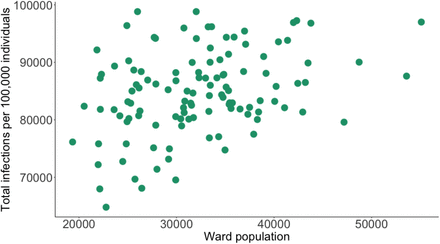
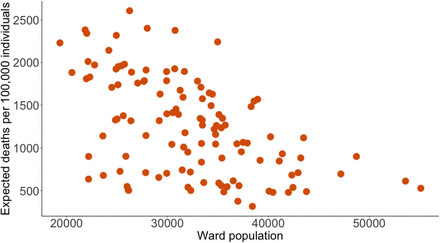
In Figure 6, we show a scatter plot of total infections across wards population. There is a strong positive relationship between number of infections and ward population size. A few features of our model and our setting contribute to this. Firstly, the most prevalent travel destination for work and school is the ward where an individual lives and as a result, wards with large populations have a large extent of within ward travel which leads to the spread of the virus. Secondly, the elderly tend not to live in high-population wards–there is a striking correlation of -0.56 between the ward level population and the number of individuals aged 60 and above. Rather, high population wards are characterized by younger inhabitants who have far greater travel probabilities and numbers of contacts which then drive higher infections in high-population wards. As a result of younger individuals living in wards with larger populations and the elderly living in less populated wards, the relationship between expected deaths and population size is inverse to the relationship between infections and population size, with a clear negative correlation between ward population and expected deaths with high population wards having less deaths than low population wards, as show in figure 7.
Simulated Covid-19 infections by ward population
This figure shows a scatter plot of the relationship between total infections within a ward and the population size of that ward from our no-intervention model. These results show mean effects from a simulation of 100,000 agents across 21 random seeds. We scale the y-axis to show incidence per 100,000 individuals.
Simulated Covid-19 expected deaths by ward population
This figure shows a scatter plot of the relationship between total expected deaths within a ward and the population size of that ward from our no-intervention model. These results show mean effects from a simulation of 100,000 agents across 21 random seeds. We scale the y-axis to show incidence per 100,000 individuals.
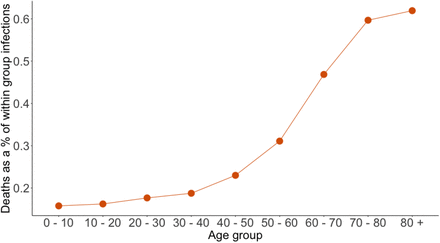
In Figure 8 we show the predicted number of deaths within age groups in our model as a share of within-age-group infections. The probability of death per infection rises significantly with age. Two features of the model contribute to this. First, the elderly have a higher probability of death and as a result, conditional on being infected, are more likely to die than any other age group. Second, while the elderly do not travel very often, they do have a far higher rate of contact with younger individuals in our model, as illustrated in Table 2. As a result of this feature, the elderly come into contact with younger individuals frequently, who effectively act as vectors of the virus.
Expected deaths as a share of all infections by age group
This figure shows the number of expected deaths per age group as a percentage of the total infections within that age group from our no-intervention scenario. These results show mean effects from a simulation of 100,000 agents across 50 random seeds.
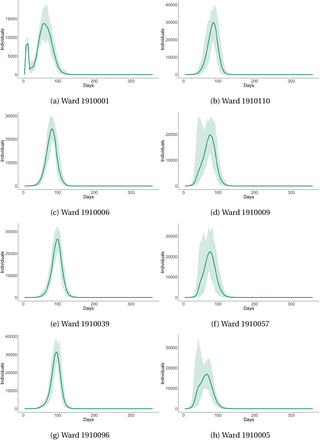
Lastly, another key feature of our model is the ability to generate ward level infection curves. To illustrate these curves, we have picked eight different ward level curves in Cape Town, shown in Figure 9. There is considerable variation in the peak, duration, shape and number of deaths across wards. This variation arises from the location of initial infections, the age-based composition of the households within a ward, and their accompanying social contact matrix and travel patterns.
Covid-19 infections by Ward
This figure shows the number of infections within eight randomly selected wards in Cape Town across our no-intervention scenario simulation, scaled to show within ward infections per 100,000 individuals. Shaded areas represent the 5% confidence interval.
4.1.2 Lockdown interventions
In the previous subsection, we show results assuming no intervention on the part of the government. However, a key feature of the Covid-19 pandemic in nearly every country has been the implementation of a lockdown. Lockdowns involve regulations that require the use of personal protective equipment such as masks together with stringent restrictions on the movement of people outside of their homes. One of the central themes of this paper is the observation that the implementation of the movement restrictions associated with lockdown are likely to be less binding in countries where large parts of the population live in informal settlements; where urban density, a lack of access to water and sanitation resources within the home, and informal and often temporary residential structures hinder the effectiveness of lockdowns.
To better understand these dynamics, we simulate two model scenarios, both of which include the implementation of a lockdown throughout the simulation. The first scenario, which we refer to as an ineffective lockdown, represents a scenario in which households that live in informal districts are constrained in their ability to adhere to lockdown restrictions, mimicking the reality in developing countries. The second scenario, which we simply refer to as a lockdown, represents a scenario where households face no constraints on their ability to adhere to lockdown restrictions, mimicking the reality in developed countries.
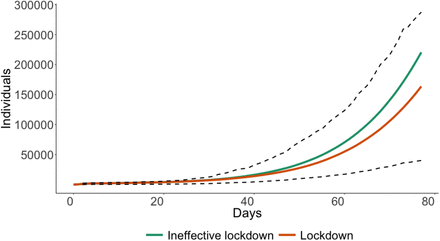
In Figure 10, we show results from our model across the three scenarios. We also report key model outcomes across scenarios in Table 4. The ineffective lockdown reduces peak infections from 741,243 in the no-intervention scenario to 393,061, a reduction of 47%. In addition to reducing peak infections, the ineffective lockdown also reduces total infections from 3.19 million in the no-intervention scenario to 2.54 million, a reduction of 25%. Despite the effectiveness relative to the no-intervention scenario, the ineffective lockdown cannot prevent the health care system from becoming overburdened; critical cases still exceed hospital capacity (i.e. they do not “flatten the curve” sufficiently). However, unlike the no-intervention scenario where peak critical cases exceed hospital beds by over 300%, the ineffective lockdown reduces the extent of overburdening my more than half, as peak critical cases exceed hospital beds by 131%. The ineffective lockdown is also successful in reducing the number of expected deaths from 44,536 in the no-intervention scenario to 33,061, a reduction of 26%. Lastly, the ineffective lockdown also significantly changes the timing of both peak infections when critical cases begin to exceed the hospital capacity. Whereas peak infections in the no-intervention scenario are reached on day 82 (June 19th) and critical cases begin to exceed hospital capacity on day 55 (May 23rd), the ineffective lockdown moves the date of peak infections to day 124 (July 23rd) with critical case beginning to exceed the hospital capacity by day 95 (June 29th).
Model outcomes across scenarios
This table depicts model outcomes for (i) total infections, (ii) total expected deaths, (iii) peak infections (iv) peak critical cases and (v) day of peak infections, across three different model scenarios, namely a no-intervention scenario, an ineffective lockdown and a normal lockdown, all simulated with 100,000 agents. We report three values for each scenario: Min represents the model output from the seed with the lowest value for each outcome; Max represents the model output from the seed with the highest value for each outcome and; Mean represents the model output taken as an average across 50 seeds for each outcome. We scale all values to the Cape Town population.
Aggregate infections, critical cases and expected deaths across scenarios
This figure shows simulated (i) infections, (ii) critical cases, and (iii) expected deaths across 3 model scenarios, namely a no-intervention scenario, an ineffective lockdown and a normal lockdown. The line shows mean effects from a simulation of 100,000 agents across 50 random seeds. We scale the y-axis to the Cape Town population. In sub-figure (b) we include a horizontal line indicating the hospital bed capacity of 3,433 beds.
The average R0 for the informal lockdown is 1.52 and 1.57 for the formal lockdown with standard deviations of 1.64 and 1.52 respectively. We note that, while it might be surprising that the R0 for the ineffective lockdown is lower than that of the effective lockdown, the difference is small. Furthermore, there is a big chance that an agent that is initially infected does not live in a ward with a high informality score.
This clearly suggests that even when a lockdown is implemented in a developing world city with large informal settlements, it remains successful at reducing infections, critical cases and expected deaths. However, to what extent does the informality affect the effectiveness of a lock-down down? In Figure 10 and Table 4, we also include the results from a lockdown scenario without any constraints on the ability of households to adhere to lockdown restrictions. When compared to the ineffective lockdown, the lockdown scenario results in fewer total infections, fewer peak infections, fewer peak critical cases and fewer expected deaths. While the difference in total infections and total expected deaths are more modest, 7.4% and 9%, respectively, the lockdown scenario results in a much larger decrease in peak infections and peak critical cases of 20.8% and 21.3%, respectively. This suggests that the largest effects of informality on disease progression–when compared to a scenario with no informality–are with respect to the number of infections that occur at the peak of the virus. This is especially important in developing countries, which typically have reduced hospital capacity when compared with developed countries.
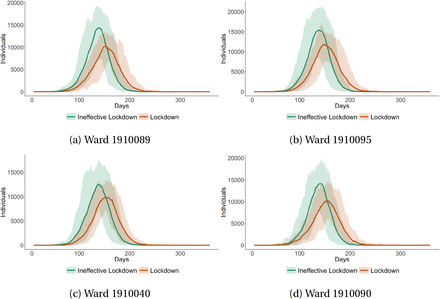
Given different wards have different levels of informality, it is natural to expect that there is strong ward-level variation in the number of infections between wards with differing levels of informality. In Figure 11 we show total infections across both the lockdown and ineffective lockdown scenarios for the four wards in Cape Town which display the highest levels of informality. There is clear variation in infections across the two scenarios which mirrors the pattern we observe in city-wide infections in Figure 10.
Infections in informal wards across different lockdown scenarios
This figure shows the number of infections within the four wards in Cape Town which have the greatest extent of informality across our ineffective lockdown and lockdown scenarios, scaled to show within ward infections per 100,000 individuals. Shaded areas represent the 5% confidence interval.
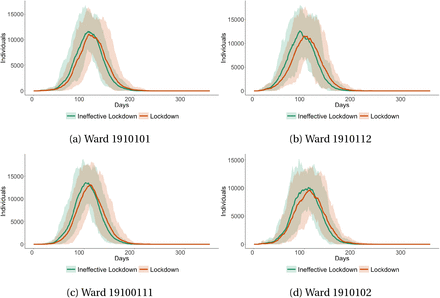
In contrast, Figure 12 shows total infections across four wards in Cape Town with no informality. In this case, there is much less of a difference between the two scenarios, to be expected, given the lack of informality. On a city-wide level, the correlation between the difference in ward level infections in the ineffective lockdown and lockdown scenarios and ward level informality is 0.5. In other words, the more informal a ward is, the greater the number of infections in the ineffective lockdown scenario relative to the lockdown scenario. Importantly, despite no informality, there will always be a difference between the two scenarios as a result of travel in the model when inhabitants from informal wards who are infectious, come into contact with inhabitants from formal wards.
Infections in wards without any informality across different lockdown scenarios
This figure shows the number of infections within four wards in Cape Town which have no informality across our ineffective lockdown and lockdown scenarios, scaled to show within ward infections per 100,000 individuals. Shaded areas represent the 5% confidence interval.
Our findings suggest that, while lockdowns are effective at reducing the number of infections, the overburdening of the healthcare system and the expected number of deaths, the informality of many districts in an emerging market city like Cape Town, significantly limits the over-all efficacy.27 In fact, when comparing the percentage difference in total ward-level infections between the same ward in a lockdown and ineffective lockdown scenario, we find a positive correlation of 0.5 between percentage difference in deaths across a lockdown and ineffective lockdown and the level of informality of the ward.
4.2 Model validation
Our validation consists of two aspects. First, we compare our results to those produces by a standard deterministic, aggregate, ordinary differential equation based model (which we denote the DE model). This is important because these are currently the workhorse model on which most predictions are based. We judge our model to be sufficiently validated if the differences in predictions can be explained by the added features of our model. Our second validation part concerns comparing our results to observed data. Here, validation means the rough reproduction of the observed reality in Cape Town for our period of reference from March 29th to June the 14th. For this period, we compare observed infections to those predicted by the model, where we consider the model validated if its predictions are larger than observed infections and smaller than a pre-lockdown estimate of non-detected infections.
4.2.1 Comparing the no-intervention scenario to a standard ODE model
Both SABCOM and the DE model use the same compartmentalized disease structure (seven compartments, described in Section 2.1) and the same age distribution (Across nine age categories).28 Moreover, the models use identical parameters wherever possible. Thus, both models use the same parameters that describe the clinical progression of the disease, including the various tenures in different disease compartments, the probabilities of transition across different compartments,and the parameters that control the severity and mortality of the disease depending on whether the health system is over capacity or not. Both models use the best empirical estimates of contact matrices to calibrate the extent of contact between individuals of different age groups. Both models use all of the clinical parameters in Table ?? and the basic reproductive rate of the disease, R0 = 3.7.
The most important difference between our model and the DE model is the geo-spatial features of our model that are both individual and district specific. In the DE model, there is an assumption of perfect mixing within any compartment. This means, for instance, that the likelihood of transmission of the disease between any susceptible individuals and any infectious individuals depends only on the age structure of average contact probabilities and the basic infectiousness of the disease. In our model, the likelihood of transmission depends on these features as well as the geographic location of each individual, and the typical geo-spatial patterns of contact between individuals in each location. See Appendix C for the details on the DE model derivation and solution.
The two model predictions (in the no-intervention scenario) differ along three important dimensions: the DE model predicts an earlier turning point (day 64) relative to our model (day 82). The DE model predicts that a larger fraction of the total population will eventually be infected (92.5%) than in our model (85.3%), but the DE model predicts fewer deaths (37179) than our model (44536). Table 5 presents the comparative figures from the two model types.
Comparison of model results
This table documents differences between SABCoM and the closest deterministic Differential Equation (DE) model without spatial features.
These differences highlight how important it is to consider “bottom-up” models such as our model with realistic spatial features in conjunction with “top-down” models such the DE model presented here. Due to the assumption of perfect mixing within the population, the DE model predicts a much faster and wider spread of the disease than our model, where the realistic structure of the spatial dispersion of the population and their connections serves to both slow the spread down.
This is important for policy makers who face complex trade-offs between the socio-economic costs of large scale interventions and the benefits of curbing the spread of a disease. For instance, using the DE model may lead to overly optimistic conclusions about the turning point and eventual mortality rate of the epidemic which might result in a premature lifting of restritions.
SABCOM has a clear advantage, in how different types of policy interventions can be modelled. In the DE model, there is only one way of considering the impact of policy on the spread of the disease: all policy actions, whether it be the enforcement of the wearing of masks or a lock-down, must be translated into impacts on R0. This has two drawbacks: (i) the DE model cannot allow for differentiation in possible outcomes between very different policy action types and (ii) the estimation of the impact of a given policy on the R0 is extremely difficult whenever a novel disease occurs. The decisive advantage of the “bottom-up” approach that considers explicitly the behavior of individuals is that policies of different types can be directly translated into impacts on a specific behavioural parameter. Moreover, the impact of a policy can be allowed to be dependent on geographic and/or socio-economic characteristics.
An example illustrates this well: a lockdown has an ex-ante uncertain impact on the R0, one which can only be fully known with a relatively long lag. The impact of a lockdown on movement patterns can, by contrast, be measured in real-time (e.g. using Google mobility data) and be directly translated into a proportional parameter of our model. We study such applications section 4.1.2.
4.2.2 Comparing intervention scenarios to observed infections
In order to further validate our model’s predictions, we can compare infections produced under our model with realized infections in Cape Town. Our challenge here relates to the extent of undetected cases in Cape Town-. While our model assumes full detection of cases, many cases will go undetected in reality, given limitations on testing resources. As a result, model predictions should exceed realized detected cases. To account for this, we compare our model prediction to two time series, the first being detected cases and the second being detected cases adjusted upward to account for undetected cases. No current estimates exist for the extent of detection in Cape Town, and as a result, we consider evidence from China which shows a detection rate of 14% pre-lockdown (Li et al., 2020). We assume that while it is reasonable to assume 14% pre-lockdown detections in South Africa as well, this number should have gone up as the South African government scaled up testing efforts. Hence, detected cases multiplier by 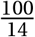 is our upper boundary for the validation. We show this comparison of cumulative infections in figure 13.
is our upper boundary for the validation. We show this comparison of cumulative infections in figure 13.
Model prediction compared to realized cases
This figure shows the number cumulative infections produced by our model under a lockdown and ineffective lockdown scenario. We include two dotted lines, the lower of which indicates realized cumulative cases from the Western Cape and the upper of which indicates realized cases assuming only 14% of cases are detected, as per Li et al. (2020). These results show mean effects from a simulation of 100,000 agents across 50 random seeds. We show the first 78 days of the simulation which correspond to the most recent infection case data at the time of writing.
Our model predicts cumulative infections that exceed realized cases but are very much in line with detection rates of 14%-25%, consistent with estimates from the literature. As such, our model is able to produce realistic infection numbers for Cape Town. Notably, both the informal and regular lockdown scenarios are validated using this approach while the no-intervention scenario produces too many infections. Indicating that the lockdown has been effective.
4.3 Sensitivity analysis of uncertain parameters
As noted in the Section 3, there are four uncertain parameters in our model which we were not able to calibrate due to the lack of available data: the likelihood to self-isolate 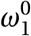 , travel restrictions
, travel restrictions 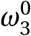 , assembly bans
, assembly bans 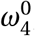 , and behavioural interventions π(Pi, Xi ; Pj, X j). As a result, we have calibrated these parameters manually so that our predicted number of infections is in line with the observed number for Cape Town.
, and behavioural interventions π(Pi, Xi ; Pj, X j). As a result, we have calibrated these parameters manually so that our predicted number of infections is in line with the observed number for Cape Town.
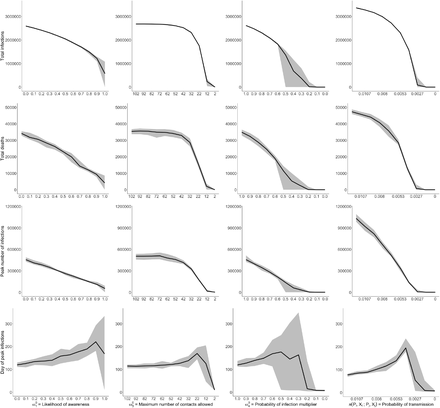
In this section, we explore the impact of these choices on our results by performing a local sensitivity analysis on each of these parameters.29 We perform the sensitivity analysis by simulating the ineffective lockdown scenario while varying the policy parameters and studying the effect of this variation on key model outcomes: ω1 ∈ [0, 1], ω2 ∈ [0, 1], ω4 ∈ [2, 100], and π(Pi, Xi ; Pj, X j) ∈ [0.0, 0.012] (i.e. ±100% of the value manually calibrated to match observed infections). We show the results from this exercise in Figure 14.
The effect on model outcomes from variation in policy parameters
This figure shows the sensitivity of four model outcomes (a) total infections (b) expected number of deaths (c) peak infections and (d) the day of peak infections in response to variations in the four model parameters: ω1 = the likelihood of awareness, π(Pi, Xi ; Pj, X j) = the probability of transmission, ω3 = the maximum number of contacts allowed and ω4 = the probability of infection multiplier, for the ineffective lockdown scenario. We vary each (i) policy parameter from 0 to 1 (ii) the maximum number of contacts from 2 to 100 and (iii) the probability of transmission by 100% from it’s calibrated value, between the range of 0 and 0.012. These results show mean effects as well as maximum and minimum values from a simulation of 100,000 agents across 10 random seeds. The y-axis is scaled up to the population of Cape Town. For each sub-figure, we keep the y-axis fixed, for readability and comparison across parameters.
There are a range of interesting relationships between parameter values and expected outcomes for total infections, number of deaths, peak infections and the day of the peak infection. In particular, there are a number of non-linear relationships, with particularly sensitive parameter ranges where small changes can have the biggest impact.
First, the likelihood of self-isolation has a strong linear relationship with all outcome variables but there is a distinct kink at 0.9 and a heightened elasticity with respect to outcome variables, most visible with total infections. For example, increasing the likelihood to self-isolate from 0.8 to 0.9 reduces total infections from 1,496,878 to 1,216,818 (a reduction of 19%) while the same magnitude of a change from 0.9 to 1 reduces total infections from 1,216,818 to 573,417 (a reduction of 53%). Interestingly however, the relationship with deaths is much more linear and 4,141 deaths still occur even when all symptomatic agents self-isolate. This highlights the important role of asymptomatic individuals who carry the disease: even if all symptomatic agents self-isolate from non-household contacts, they can still infect members of their households, who, if asymptomatic, then proceed to travel and spread the virus (in the model, around 39% of all infections are asymptomatic). This has important policy implications as it suggests that a combination of contact tracing and widespread testing which can diagnose symptomatic individuals and identify and test individuals who have had social contact with these individuals (even if asymptomatic) can be effective at reducing asymptomatic transmission.
Second, assembly bans are particularly effective at reducing infections and deaths around a ban of 20 people. Increasing the assembly ban by 10 from 12 to 22 people reduces total infections from 1,759,697 to 233,797 (a reduction of 86%). These restrictions, however, stop being effective at more than roughly 50 people.
Third, the calibrated value for the probability of infection during the lockdown in the presence of informal neighborhoods–interpreted as a travel restriction–is between 0.91 and 0.97. In this region, travel restrictions are not particularly effective and a reduction from 0.9 to 0.8 only leads to a reduction in the expected number of total infections from 2,478,549 to 2,302,650 (a reduction of 7.1%). By contrast, the same reduction from 0.6 to 0.5 reduces the expected number of total infections from 1,828,698 to 1,365,659 (a reduction of 25.3%). Interestingly, the virus dies out entirely at a value of 0.2 (as opposed to 0).
Finally, we also study variations in the the probability of transmission. Across all of the parameters, the probability of transmission has the greatest variability, especially at larger parameter values. Despite, these changes being large in relative terms, they are small in absolute terms, and these small absolute changes can result in large changes in outcomes. This highlights the importance of correctly estimating this key paramater for policy analysis, as small variations can lead to sizeable differences in expected outcomes.
5 Conclusion
We have presented the Spatial Agent-Based Covid-19 Model (SABCoM). The main purpose of the model is to deliver district level Covid-19 predictions about infections, ICU capacity and fatalities. These predictions can be used by local politicians and health care managers to support hospital capacity planning during the pandemic.
In this paper, we have shown how SABCoM can be used by applying it to the city of Cape Town, a city that is characterized by a high degree of inequality and has several informal districts. Using our calibration, we show that the model predictions about infections are well in line with what we observe in the data, especially when we take into account lockdown policies and the existence of informal districts. For Cape Town, assuming that current lockdown policies remain in place, our model predicts that after a year between 67% (2,518,977) and 69% (2,581,759) of the population will have been infected, and between 30,998 (0.8%) and 35,822 (1%) citizens will have died. The peak of infections is projected to occur between the 16th of August and the 5th of September, under an inefficient lockdown scenario–which is the most realistic scenario for Cape Town–while health system capacity is projected to be breached between the 17th of July and the 25th of September.
We believe that this model will be a valuable addition to the health care decision makers toolkit. Our validation exercise confirms that the model has been able to explain observed infections in Cape Town in the period from 29th of March 2020 to Sunday the 14th of June and that the predictions of our model compare well to popular SEIR ordinary differential equation models.
We decided to report ranges rather than only means, as we agree with Saltelli et al. (2020), that there is no substantial aspect of this pandemic for which any researcher can currently provide precise, reliable numbers. Like all models, our model relies on a large number of uncertain inputs and structural assumptions. As our sensitivity analysis has shown, the most important of these parameters are the probability of transmission when two persons meet and the uncertain lockdown policy parameters.
Our model is, to the best of our knowledge, the only available bottom-up model to study the transmission of Covid-19 in South Africa. While we apply our model to Cape Town, we provide all code and replication files in our software repository on github so that it is easy to replicate our analysis for other cities.
Data Availability
All data and scripts are available on Github
Nomenclature
βemp Set of empirical moments
βsim Set of simulated moments
δL Health system overburdened multiplier
F ca Observed cases per district
F hc Observed age group household contacts
F in Observed cases per district
F oc Observed non-household contacts
F pop Observed district population
F tv Observed travel matrix
γ Size of overlap between a ward and a region
𝒮 set of all age groups
ℰ Edges
ℊ Undirected graph of interactions
ℋ Set of households
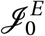 Set of agents that are infected at the start of the simulation
Set of agents that are infected at the start of the simulation
𝒩 Nodes in network, representing the total number of agents
𝒲 Set of districts (known as wards in South Africa)
N oc Number of non-household connections of agents
ω1 Likelihood that an agent is aware that she has the virus
ω2 Fraction of travel network connections that are active for each agent
ω3 maximum number of non-household contacts any agent is allowed to have each day
ω4 Policy multiplier that can decrease the probability of infection
π(Pi, Xi ; Pj, X j) Base probability of infecting another agent
πas probability to enter asymptomatic state
πC,s probability to enter critical state when symptomatic πD,s Probability to enter deceased state when symptomatic τas Recovery period asymptomatic infection
τs Transition period symptomatic infection
τE Latency period
a specific age group
as asymptomatic
C Critically ill status
D Deceases status
E Exposed but not infectious status
fi,j Travel flows between two districts
h Household
i Informality level (applied to districts)
Is Infectious and symptomatic status
Ias Infectious but asymptomatic status
j an individual agent
L Health system capacity
M Total number of Monte Carlo simulations
m seed used for individual Monte Carlo simulation
P Epidemiological status
R Recovered status
S Susceptible to infection status
s Symptomatic
T Total simulation time
t Single time period representing a day
w specific district (Ward)
w′ travel destination district (Ward)
F hs Observed district household size distribution
Appendix A Data appendix
All data used in this paper is publicly available. In this section, we outline the data used in this paper and provide information of how the data can be downloaded.
Fca: Observed cases per district
–Source: Western Cape Government
–Each day, the Western Cape government releases a pdf report documenting the number of cases spatially. These reports can be found here
–We transcribe these cases for each sub-district by hand for each day. A sub-district is a larger spatial definition than the wards we use in this paper.
–We then overlay our wards on the sub-districts and assign wards to sub-districts.
–Finally, we assign sub-district level infection cases to wards based on a probability calculated as the ward level population normalized by the sub-district level population.
Fhc : Observed age group household contacts
–Source: Prem, Cook and Jit (2017)
–Data can be downloaded from the journal website, here
Foc : Observed non-household contacts
–Source: Prem, Cook and Jit (2017)
–Data can be downloaded from the journal website, here here
F pop : Observed district population
–Source: 2011 Census from Statistics South Africa
–Data can be downloaded from Statistics South Africa’s website, after the creation of a free profile, here. Once you are logged in, navigate to Community Profiles > Census 2011 (2016 Boundaries) in the sidebar
FTV : Observed travel matrix
–Source: 2013 National Household Travel Survey from Statistics South Africa
–Data is obtained from DataFirst. Data can be found on the DataFirst data portal, here. You will need to create an account to access the data.
–We discuss the steps taken in mapping this data to our ward spatial structure in Appendix B.
Fhs: Observed district household size distribution
–Source: 2011 Census from Statistics South Africa
–Data can be downloaded from Statistics South Africa’s website, after the creation of a free profile, here. Once you are logged in, navigate to Community Profiles > Census 2011 (2016 Boundaries) in the sidebar
F in: Informality level
–Source: 2011 Census from Statistics South Africa
–Data can be downloaded from Statistics South Africa’s website, after the creation of a free profile, here. Once you are logged in, navigate to Community Profiles > Census 2011 (2016 Boundaries) in the sidebar
Appendix B Travel calibration
In order to calibrate our model to realistic travel patterns, we use the 2013 National Household Travel Survey, a nationally representative travel survey. Importantly, for our purposes, the survey records where respondents live, where they travel to for work and/or education, the frequency of travel, and the time spent travelling. The travel survey allocates respondents to travel regions of which there are 18 in Cape Town. Our challenge then is to relate the 116 wards we use in this paper, to the 18 travel regions. We illustrate a simplified schematic of how these two structures relate in Figure 15.
Travel data illustrative schematic
This figure illustrates how the travel survey data we use corresponds to wards, our geo-spatial structure. The travel survey data records flows of people between regions. Respondents are asked in which region they reside and then in which region they commute to for work and/or education reasons. There are 18 regions in Cape Town, while there are 116 wards. In this illustrative schematic, we have 3 regions where travel only occurs between Region 1 and Region 2, and between Region 3 and Region 2. In some cases, wards will fit perfectly into a single region as is the case with Wards 2 through 5. However, there may be a case where a ward overlaps with two regions as is the case with Ward 1 which overlaps Regions 1 and 2.
Our goal is to create a ward-level travel probability matrix using the regional travel data. To implement this, we allocate region level flows to wards in proportion to the size of the both the origin and destination ward population as a share of their respective total regional population.
We illustrate this process in Figure 16.
Mapping region-based travel data to ward
This figure illustrates how we map the travel survey data we collect to wards, our suburb structure. We allocate region level flows to wards in proportion to the size of both the origin and destination ward population as a share of their respective total region population. γ reflects the percentage overlap between a ward and a region, in the case of an overlap. fi,j represents flows between regions. δi,i represents the share of survey respondents who both live and work / attend school in region i and who have an average travel time that is above the 25th percentile of the travel time distribution of all individuals who both live and work / attend school in region i.
There are three scenarios which we encounter. The first involves travel between two wards, which are both perfectly located within two different regions, as is the case between Ward 2, located in Region 1, and Ward 3, located in Region 2. We construct the flow of people between these wards as the product of:
 : The size of Ward 2’s population relative to the total population of Region 1;
: The size of Ward 2’s population relative to the total population of Region 1; : The size of Ward 3’s population relative to the total population of Region 3;
: The size of Ward 3’s population relative to the total population of Region 3;f1,2: The flow of people between Region 1 and Region 2;
We introduce a parameter γ which scales the population of Ward 1, 𝒩1. This accounts for a scenario where Ward 1 overlaps with two regions, as is illustrated in Figure 15. γ then reflects the percentage geographic overlap between Ward 1 and Region 1. We use this geographic overlap to assign the ward population to the respective region.30
Our second scenario involves travel between two wards, in which only one ward is perfectly located within a region, as is the case between Ward 1, located in Region 1 and Region 3, and Ward 3, located in Region 2. In this scenario, we map two flows31
 : The flow of people from the part of Ward 1 located in Region 1;
: The flow of people from the part of Ward 1 located in Region 1; : The flow of people from the part of Ward 1 located in Region 3;
: The flow of people from the part of Ward 1 located in Region 3;
Our third scenario represents a case where a respondent reports living and working/attending school in the same region. Within this scenario, we need to decide how to assign respondents who are likely to live and travel within the same ward versus respondents who are likely to live in one ward, but travel to another ward within the same region. In our illustrative example, such as case occurs between Ward 1 and Ward 2 and between Ward 1 and Ward 5. In order to allocate these flows, we introduce a new parameter δi,i which takes a value between 0 and 1, indicating the likelihood that an individual respondent lives and works / attends schools in different wards within the same region.
We leverage a question in the travel survey, which asks how much time a daily commute takes. Using this question, we take the distribution of travel times for all respondents who live and work/attend school in the same region and assign any individual who has a travel time greater than the 25th percentile of this distribution as a cross-ward traveller, assigning the rest of respondents as within-ward travellers. δi,i then reflects the share of within region travellers, who are likely to be cross-ward travellers. The assumption here being that the likelihood of crossward travel increases with travel time. Using this, we now assign 4 travel flows for Ward 1
 : The flow of people from the part of Ward 1 located in Region 1 to Ward 2;
: The flow of people from the part of Ward 1 located in Region 1 to Ward 2; : The flow of of people from the part of Ward 1 located in Region 1 who do not travel;
: The flow of of people from the part of Ward 1 located in Region 1 who do not travel; : The flow of people from the part of Ward 1 located in Region 3 to Ward 5;
: The flow of people from the part of Ward 1 located in Region 3 to Ward 5; : The flow of people from the part of Ward 1 located in Region 3 who do not travel;
: The flow of people from the part of Ward 1 located in Region 3 who do not travel;
Following this approach, we obtain a ward-level travel flow between each ward. To convert this to travel probability, we normalize each outgoing travel flow from a given ward by the total outgoing flows from that same ward. For Ward 1 then, the probability of travelling to Ward 2 can be calculated as follows:
Flow from Ward 1 to Ward 2: fw1,w2;
Total flows from Ward 1: 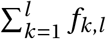
Probability of travel between Ward 1 and Ward 2: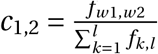 ;
;
Appendix C Benchmark: a deterministic ordinary differential equation epidemiological model
To study the differences in predictions from the geo-spatial, agent-based implementation of SABCoM, we constructed a closely comparable analytical model that is built on a mean-field approximation of a perfectly mixed population. This type of model (in its simplest form, typically called a Susceptible-Infected-Recovered or SIR model) is standard in the epidemiological literature following Kermack and McKendrick (1927). The dynamics of the disease spread are modelled via a system of deterministic ordinary differential equations (ODEs) that represent the evolution of the disease in a variety of discrete compartments that describe the populations in different stages of the disease or falling in different disaggregated categories of the population under study. Hereafter, we call the deterministic, ordinary differential equation model discussed in this section the DE model.
The DE model that we compare SABCoM to has the same 7 disease compartments32 and the same 9 age-category compartments as SABCoM, and is parameterized using the same parameters that control the disease progression where possible (see section 2), but is a simpler model as it abstracts from all geo-spatial or socio-economic characteristics. Towers and Feng (2012) presents a similar age-structured model with 4 disease compartments that employs detailed information on average number of contacts across the age distribution, and we follow their formal development closely.
The data available for Cape Town allows us to study the disease progression across the 9 age categories in the set 𝒜 = {0 − 10, 10 − 20,…, 70 − 80, 80+}. As the DE model studies the evolution of the disease in terms of the total populations in compartments (rather than from the perspective of individuals), we need to adjust the notation from the main model slightly: let Na denote the total population size in age group a and let Pa denote the total population in a specific age group, a, that are in a given disease compartment P ∈ {S, E, I as, I s,C, R, D} at a given instant in time (e.g. Sa is the number of individuals of age group a in the susceptible compartment). The DE model characterizes the instantaneous rate of change in the population in each compartment as a function of the levels of the population in each compartment.
A key feature of an age-structured SIR model is the transmission of the disease across agegroups. For this we use the best estimates of the average number of daily contacts across individuals in different age-groups organized in a contact matrix (see appendix A for details on this data). In SABCoM, we use sub-components of the contact matrices across different activities: the number of daily contacts within household (F hc) and non-household contacts (F oc) in the construction of the spatially explicit network of connections across the city. For our comparison DE model, we do not consider household structure or spatial aspects, so we only use the total number of contacts: F c = F hc + F oc. The typical entry of the contact matrix, 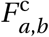 is the average number of daily contacts someone in age group a has with someone in age group b.33
is the average number of daily contacts someone in age group a has with someone in age group b.33
We model the evolution of the disease with the following system of ODEs :
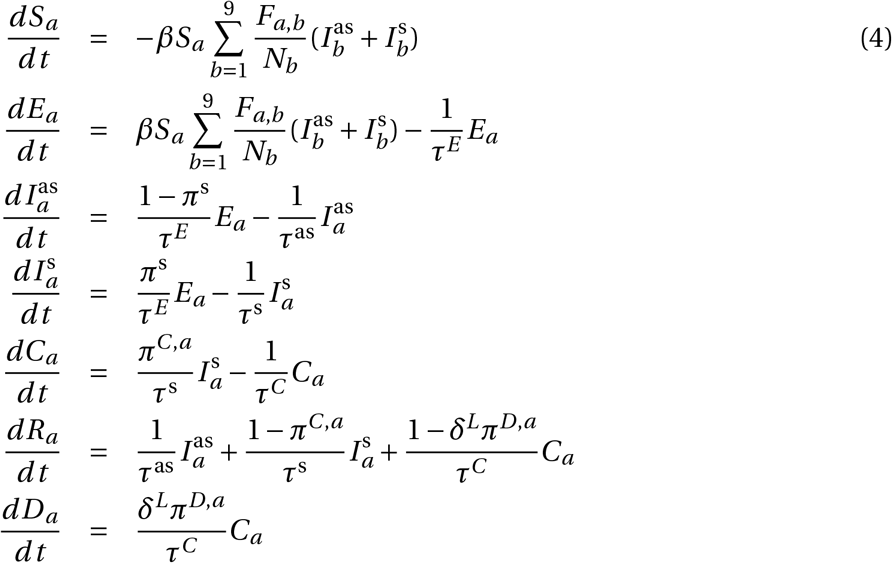 In this model, β is the basic rate of transmission of the disease conditional on contact between a susceptible and an infectious individual (the closest DE model equivalent to π(Pi, Xi ; Pj, X j) in SABCoM). In the present calibration, symptomatic and asymptomatic are modelled as equally infectious. Typically, SIR models are specified in terms of instantaneous exit rates (γ) from compartments, rather than average tenure in compartments (τ). In the mean-field approximation, however, the exit rate γP from disease compartment P is equal to the inverse of the average number of days spent in the compartment, which is the deterministic primitive parameter of used to calibrate SABCoM, thus:
In this model, β is the basic rate of transmission of the disease conditional on contact between a susceptible and an infectious individual (the closest DE model equivalent to π(Pi, Xi ; Pj, X j) in SABCoM). In the present calibration, symptomatic and asymptomatic are modelled as equally infectious. Typically, SIR models are specified in terms of instantaneous exit rates (γ) from compartments, rather than average tenure in compartments (τ). In the mean-field approximation, however, the exit rate γP from disease compartment P is equal to the inverse of the average number of days spent in the compartment, which is the deterministic primitive parameter of used to calibrate SABCoM, thus:  . Therefore, except for β, the values of all parameters of the model presented in equation (4) are set to the same values as in the SABCoM implementation (see table 1 for the definitions, values and sources of each of the parameters).
. Therefore, except for β, the values of all parameters of the model presented in equation (4) are set to the same values as in the SABCoM implementation (see table 1 for the definitions, values and sources of each of the parameters).
To compare the predictions of these very different type, we set β such that the implied basic reproductive number (R0) of the DE model matches the estimated average R0 of the SAB-CoM baseline calibration. Following the results in Towers and Feng (2012) and Blackwood and Childs (2018), the R0 of the DE model above is deterministically related to β: it is equal to β (τas + πs(τs −τas)) times the dominant eigenvalue of the matrix of standardized contact frequencies 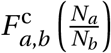
We solve the differential equations in (4) numerically34 and compare the results to the average outcomes in the stochastic simulations of SABCoM in section 4.2.
Footnotes
* We thank Peter Courtney for his excellent research assistance. The source code and replication files for this paper can be found here. All errors are our own.
↵1 See “Statement by President Cyril Ramaphosa on measures to combat Covid-19 epidemic.” Available here and accessed 6 July 2020.
↵2 Hale et al. (2020) develop a lockdown stringency index which scores lockdowns worldwide on a 0-100 scale where 0 is the least and 100 is the most stringent lockdown. In response to the Covid-19 outbreak, South Africa went into a 87.96 stringency index lockdown.
↵3 Details on level 4 regulations can be found here.
↵4 Details of level 3 regulations have been announced in Government Gazette here by Department of Cooperative Governance and Traditional Affairs Minister Nkosazana Dlamini-Zuma.
↵5 These numbers are higher than the current official estimate, which is likely due to our use of the epidemiological data by Verity et al. (2020), which has been updated in the official predictions.
↵6 As an upper bound, we use evidence from China which shows a detection rate of 14% pre-lockdown (Li et al., 2020).
↵7 We sometimes refer to physical interactions as social connections.
↵8 We use the convention that sets are denoted by formal script, e.g. 𝒩 ; the value of a variable (such as the cardinality of a set) are denoted by upper case letters (e.g. N ≡ |𝒩 |), and generic elements are denoted by lower case letters (e.g. an agent is denoted as j ∈ 𝒩). Indices denoting generic elements of a set are subscripts, while additional identifiers are superscripts.
↵9 The epidemiological literature denotes these values as compartments and we follow this nomenclature on occasion.
↵10 We use this simplifying assumption to model the situation where patients who are isolated in hospital cannot spread the disease in their regular social networks.
↵11 We construct the empirical distribution of households sizes for each district from the most recent data on on numbers of households of each observed size in each district taken from the 2011 South African Census which we provide as ancillary information to this paper in data file F hs. Naturally, since the algorithm is stochastic, and we use representative agent populations smaller than the actual populations in the city modelled, there are some additional algorithmic features that ensure that (i) the maximum household size randomly drawn remains smaller than remaining number of agents to be assigned to a household at every point in the algorithm, and (ii) that the final number of agents in a district correspond to the proportional size of that district given the ratio of total modeled agents to actual population of the city.
↵12 Different implementations of our model will use different data sources, and hence different algorithms for constructing agent populations. We use data from the 2011 National Census undertaken by Statistics South Africa to obtain a realistic age-structure of households for Cape Town. We supplement this data with an age-group contact matrix for household contacts for South Africa which we obtain from Prem, Cook and Jit (2017). In this data, average daily contact frequencies between individuals in different age groups are recorded.
↵13 F hcis a matrix that records the best estimates of data on daily number of contacts between individuals in different age categories within the same household. It has the following structure: row a of the square matrix F hccontains the list of average daily number of contacts that an individual in age category a is expected to have with an individuals in each of the age categories represented by the columns of F hc. A probability distribution of likely contact of someone of age category a with someone of age category b is constructed by normalizing the entries of row a of F hcso that they add to one.
↵14 F ocis a matrix that records the best estimates of data on daily number of contacts between individuals in different age categories outside of the household. Its structure is identical to that of F hcdescribed in footnote 13.
↵15 See Appendix B for the details on the construction of F tv.
↵16 Without this feature, travelers to a district could only infect residents, which not a reasonable characterization of the impact of travel hubs on the spread of disease.
↵17 The algorithm is robust to implementations with smaller populations where it is possible that
 |.
|.↵18 Reflecting the fact that it is much harder to isolate oneself to purely household contacts in informal districts.
↵19 Find the code and replication files on our GitHub repository, here
↵20 The latest date for which we have survey data.
↵21 Hence, we will use the two terms interchangeably when discussing results for Cape Town.
↵22 The travel survey only asks respondents where they live, work and where they attend school. As a result, travel patterns reflect patterns related specifically to work and school and not for other reasons such as leisure or shopping, for example.
↵23 Details can be found here.
↵24 See for example: “Winde confirms pressure on hospital system increased, despite not yet hitting peak capacity” - News24, 22 May 2020
↵25 Google Covid-19 Mobility Reports
↵26 Computations were performed using facilities provided by the University of Cape Town’s ICTS High Performance Computing team (hpc.uct.ac.za) and the University of Stellenbosch’s HPC1, Rhasatsha (www.sun.ac.za/hpc).
↵27 Our paper focuses on informality as the reason for a less effective lockdown. In this case, the reasons for non-adherence to lockdown regulations are the result of circumstance and outside of the control of individuals. Despite this, our findings can be generalized to settings where individuals may voluntarily choose to disobey lockdown regulations due to reasons such as beliefs regarding the spread of Covid-19 or societal unrest.
↵28 This entails that the DE model has 63 compartments.
↵29 Keeping all other parameters fixed.
↵30 The inherent assumption here being that the ward level population is distributed evenly across the ward.
↵31 In the event that the destination ward also overlaps multiple regions, we can modify these flow equations with an additional overlap parameter which scales the destination wards population.
↵32 Susceptible (S), Exposed but not infectious (E), Infectious but asymptomatic (I as), Infections and symptomatic (I s), Critically ill but isolated (C), Recovered and immune (R), and Deceased (D)
↵33 The contact matrix need not be symmetric, as the population sizes of different age groups differ. When modelling a closed population in an SIR model, however, it must respect reciprocity:
 (the total contact time between two age groups must be the same measured from either perspective). Since the empirical estimates of contact rates constructed from survey data typically do not satisfy this condition naturally, we employ the reciprocity correction suggested by Towers and Feng (2012):
(the total contact time between two age groups must be the same measured from either perspective). Since the empirical estimates of contact rates constructed from survey data typically do not satisfy this condition naturally, we employ the reciprocity correction suggested by Towers and Feng (2012):  , where
, where  is the raw, estimated contact rates constructed from the data.
is the raw, estimated contact rates constructed from the data.↵34 The model is setup and solved in file comparison_DE_model.py using the odeint package of scipy (www.scipy.org).