Abstract
The role of asymptomatic carriers in transmission poses challenges for control of the COVID-19 pandemic. Study of asymptomatic transmission and implications for surveillance and disease burden are ongoing, but there has been little study of the implications of asymp- tomatic transmission on dynamics of disease. We use a mathematical framework to evaluate expected effects of asymptomatic transmission on the basic reproduction number ℛ0 (i.e., the expected number of secondary cases generated by an average primary case in a fully sus- ceptible population) and the fraction of new secondary cases attributable to asymptomatic individuals. If the generation-interval distribution of asymptomatic transmission differs from that of symptomatic transmission, then estimates of the basic reproduction number which do not explicitly account for asymptomatic cases may be systematically biased. Specifically, if asymptomatic cases have a shorter generation interval than symptomatic cases, ℛ0 will be over-estimated, and if they have a longer generation interval, ℛ0 will be under-estimated. Estimates of the realized proportion of asymptomatic transmission during the exponential phase also depend on asymptomatic generation intervals. Our analysis shows that understanding the temporal course of asymptomatic transmission can be important for assessing the importance of this route of transmission, and for disease dynamics. This provides an additional motivation for investigating both the importance and relative duration of asymptomatic transmission.
I. INTRODUCTION
In an epidemic, symptomatic cases are the predominant focus of treatment and usually represent the bulk of reported cases. However, infected individuals who are asymptomatic yet infectious can be a critical factor in the spread of some pathogens [1]. Asymptomatic individuals are hard to trace, unlikely to self-isolate, and are likely to retain normal social and travel patterns [2].
There is significant ongoing interest in asymptomatic infections in COVID-19 [3–5] and their transmission potential [6] for two major reasons. First, the proportion of infections that are asymptomatic (see [7]) is critical to attempts to estimate the likely burden of severe outcomes (including mortality [8]) when the virus spreads through a population. Second, understanding the possible role of transmission by asymptomatic individuals is crucial to planning surveillance and control efforts [1]. Given that 86% of the cases were undocumented (i.e., mildly symptomatic or asymptomatic) in Wuhan prior to travel restrictions and may account for 79% of infection in severe, symptomatic cases [9], asymptomatic cases are also likely to play an important role in the transmission of COVID-19.
Here, we focus on a third effect. If asymptomatic cases are important for transmission, they also have the potential to affect estimates of key parameters of disease spread such as the basic reproduction number ℛ0 (i.e., the expected number of secondary cases generated by an average primary case in a fully susceptible population [10]). Thus, we investigate the relationship between individual-level features of asymptomatic cases (e.g., the probability that an infection is asymptomatic, asymptomatic case duration, transmission by asymptomatic individuals) to dynamics at the population scale.
II. METHODS
We model viral spread using a renewal-equation framework [11], which allows us to model the current incidence of infected individuals (i.e., the rate at which new infections occur in the population) as a function of previous incidence and how infectiousness of an infected individual varies over the course of their infection. We divide incidence i into two categories –ia and is – corresponding to incidence of asymptomatic and symptomatic cases, respectively. Newly infected individuals that are either asymptomatically or symptomatically infected can transmit the disease to others, but they may differ in their intrinsic reproduction numbers, ℛa and ℛs, respectively, as well as intrinsic generation-interval distributions [12], ga(τ) and gs(τ). Generation intervals, which are defined as the time between when an individual is infected and when that individual infects another person [13], shape the relationship between the epidemic growth rate r and the reproduction number [14]. The differences in the generation-interval distributions between asymptomatic and symptomatic cases can be caused by the differences in the natural history of infection irrespective of their transmissibility: Individuals with asymptomatic infections may recover faster and have short generation intervals, or have persistent infection and long generation intervals (cf. [15]).
Neglecting births and loss of immunity on the time scale of the outbreak, the dynamics of susceptibles and incidence are (see Table S1 for parameter definitions):

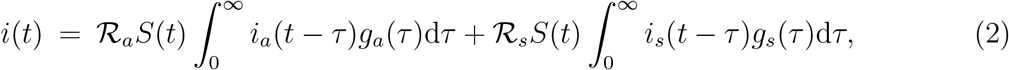 where i(t) = ia(t) + is(t). The basic reproduction number of this system is:
where i(t) = ia(t) + is(t). The basic reproduction number of this system is:
 where p is the proportion of incident cases that are asymptomatic: ia(t) = pi(t). The corresponding intrinsic generation-interval distribution of an average infected individual is given by:
where p is the proportion of incident cases that are asymptomatic: ia(t) = pi(t). The corresponding intrinsic generation-interval distribution of an average infected individual is given by:
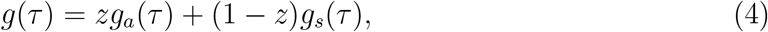 where we define the “intrinsic” proportion of asymptomatic transmission z as the relative contribution of asymptomatic cases to the basic reproduction number:
where we define the “intrinsic” proportion of asymptomatic transmission z as the relative contribution of asymptomatic cases to the basic reproduction number:

Note that the intrinsic proportion of symptomatic transmission satisfies

Yet, this information is not sufficient to disentangle the role of asymptomatic cases, i.e., what fraction of secondary cases can be ascribed to realized transmission from asymptomatic cases vs. symptomatic cases?
The intrinsic proportion of asymptomatic transmission z is a useful benchmark, but does not necessarily reflect the realized proportion of asymptomatic transmission, unless both types of infection have the same generation-interval distribution. The realized proportion of asymptomatic transmission, q at time t is given by:
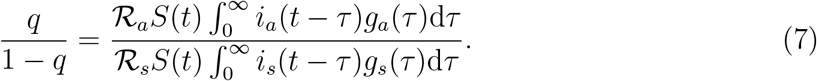
During the period of exponential growth, we assume S remains nearly constant, and i(t) is proportional to exp(rt); here, the observed exponential growth rate r is an average of the exponential growth rates we would observe if there were only asymptomatic (p = 1) or symptomatic (p = 0) cases. We then simplify by recalling that ia(t) = pi(t), is(t) = (1−p)i(t) such that:

Here, δc for each of the two classes is the average “discount” of a new infection – the average relative contribution of a secondary infection to the epidemic, taking exponential growth into account:

δc < 1 and grows smaller as the generation interval grows longer. Thus, the realized proportion of asymptomatic infections will be increased (resp., decreased) if transmission is relatively faster (slower) along the asymptomatic route. The discount δ also depends on the relative variation in the generation-interval distribution, the “dispersion”: More variation in generation intervals leads to more opportunities for fast spread and thus to higher values of δ (similar to shorter average generation intervals).
To estimate the effects of assumptions about asymptomatic transmission on the inferred importance of asymptomatic transmission and estimates of the basic reproduction number ℛ0, we parameterize the generation interval distributions of asymptomatic and symptomatic cases based on their means, 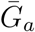 and
and 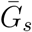 , and dispersions, κa and κs. We assume that generation intervals are gamma distributed, and we set the dispersion to be equal to the squared coefficient of variation (the reciprocal of the gamma shape parameter, see Supplementary Materials). We assume that epidemic growth rate r and the generation-interval distribution of symptomatic case are known, using parameter values that are consistent with earlier COVID-19 models [16]: 1/r = 7 days,
, and dispersions, κa and κs. We assume that generation intervals are gamma distributed, and we set the dispersion to be equal to the squared coefficient of variation (the reciprocal of the gamma shape parameter, see Supplementary Materials). We assume that epidemic growth rate r and the generation-interval distribution of symptomatic case are known, using parameter values that are consistent with earlier COVID-19 models [16]: 1/r = 7 days, 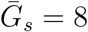 days, and κs = 0.5. We infer values of q using
days, and κs = 0.5. We infer values of q using
Eq. (8) and ℛ0 using the Euler-Lotka equation [17]:
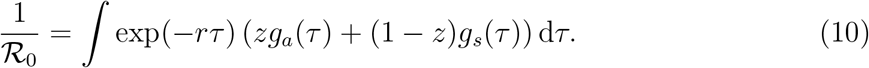
We compare this with the naive estimate of the basic reproduction number that assumes that the generation-interval distributions of the asymptomatic and symptomatic cases are identical:
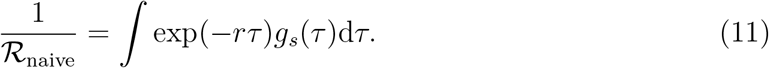
In Supplementary Materials, we also use an ordinary differential equation model (SEIR model) including both asymptomatic and symptomatic cases to give a concrete example of how differences in generation intervals affect both q and estimates of ℛ0.
III. RESULTS
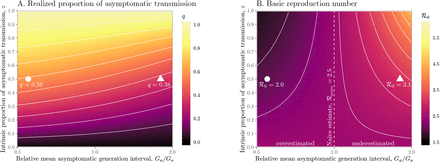
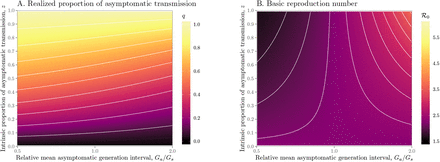
We explore the effects of different assumptions about speed and effectiveness of asymptomatic transmission on the importance of asymptomatic transmission and estimates of the basic reproduction number ℛ0, using a gamma assumption (see Methods). Across the range of parameters we explore, the intrinsic proportion of asymptomatic transmission z is similar to the realized proportion q (Figure 1A). As the relative mean generation interval of asymptomatic transmission, 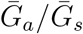 , increases, q decreases because symptomatic cases are more likely to have short generation intervals, which drive the spread during the growth phase (Figure 1A). In Figure S1, we present the same figure but showing differences between the realized and the intrinsic proportion of asymptomatic transmission, q − z.
, increases, q decreases because symptomatic cases are more likely to have short generation intervals, which drive the spread during the growth phase (Figure 1A). In Figure S1, we present the same figure but showing differences between the realized and the intrinsic proportion of asymptomatic transmission, q − z.
Effects of intrinsic proportion of asymptomatic transmission on the realized proportion of asymptomatic transmission and basic reproduction number, given variation in the mean generation interval of asymptomatic cases. (A) Increasing the speed of asymptomatic transmission (shorter generation intervals) increases the realized proportion of asymptomatic transmission, q. Increasing the speed of asymptomatic transmission (shorter generation intervals) decreases the basic reproduction number ℛ0. When 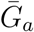 is smaller (larger) than
is smaller (larger) than 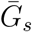 , estimates based on the observed generation distribution for symptomatic cases (ℛ0 = 2.5; dashed line) are expected to over- (under-) estimate the true ℛ0. For both panels, the circle denotes z = 0.5 and
, estimates based on the observed generation distribution for symptomatic cases (ℛ0 = 2.5; dashed line) are expected to over- (under-) estimate the true ℛ0. For both panels, the circle denotes z = 0.5 and 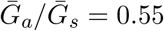 whereas the triangle denotes z = 0.5 and
whereas the triangle denotes z = 0.5 and 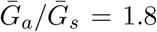 . Solid lines show contours for q and ℛ0 values. The dashed line represents the naive estimate that assumes
. Solid lines show contours for q and ℛ0 values. The dashed line represents the naive estimate that assumes 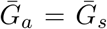 . Here, we assume 1/r = 7 days,
. Here, we assume 1/r = 7 days, 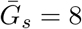 days, and κs = κa = 0.5.
days, and κs = κa = 0.5.
Figure 1B shows the effect of different assumptions about the generation interval of asymptomatic cases, 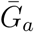 , on the estimated basic reproduction number ℛ0. When
, on the estimated basic reproduction number ℛ0. When 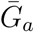 is long compared to
is long compared to  , then we are effectively assuming a longer mean for the overall generation interval. This assumption leads to a larger estimate of ℛ0 for a fixed value of r (see [18]). Conversely, when
, then we are effectively assuming a longer mean for the overall generation interval. This assumption leads to a larger estimate of ℛ0 for a fixed value of r (see [18]). Conversely, when 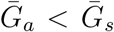 , generation intervals are shorter, leading to lower estimates of the epidemic strength ℛ0. Both of these effects are stronger when the intrinsic proportion of asymptomatic transmission z increases (and disappear as z→0). Therefore, when ℛ0 is estimated without explicitly accounting for asymptomatic spread (white, dashed line in Figure 1B), it can be over- or underestimated depending on the relative duration of infection between symptomatic and asymptomatic individuals. The qualitative effects of z and
, generation intervals are shorter, leading to lower estimates of the epidemic strength ℛ0. Both of these effects are stronger when the intrinsic proportion of asymptomatic transmission z increases (and disappear as z→0). Therefore, when ℛ0 is estimated without explicitly accounting for asymptomatic spread (white, dashed line in Figure 1B), it can be over- or underestimated depending on the relative duration of infection between symptomatic and asymptomatic individuals. The qualitative effects of z and 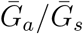 on q and ℛ0 remain robust when we assume narrower (κs = κa = 0.3; Figure S2) or wider (κs = κa = 0.8; Figure S3) generation intervals.
on q and ℛ0 remain robust when we assume narrower (κs = κa = 0.3; Figure S2) or wider (κs = κa = 0.8; Figure S3) generation intervals.
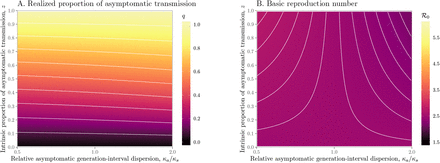
Relative generation-interval dispersion of asymptomatic cases κa/κs have similar, but smaller, effects on q and ℛ0 (Figure S4). Since a wider generation-interval distribution has a higher proportion of early transmission than a narrow one, increasing the generation-interval dispersion has qualitatively similar effects on q and ℛ0 as decreasing the mean generation interval.
IV. DISCUSSION
Much is still unknown about the time scale and effectiveness of asymptomatic transmission in COVID-19. Here we highlight the need to characterize the generation-interval distribution for asymptomatic transmission, and its consequences not only for contact tracing but for estimation of the basic reproduction number of the ongoing COVID-19 outbreak [16] and of the effective proportion of asymptomatic transmission during the exponential-growth phase. Our reproductive number findings fit into a broader framework linking epidemic speed, strength, and generation intervals – for a given observed speed increases in the mean generation interval imply larger reproduction number [14, 15, 18–20].
If asymptomatic infections are more persistent than symptomatic ones, the mean generation interval for COVID-19 could be longer than estimated from symptomatic cases alone possibly causing ℛ0 to be underestimated (Figure 1B). However, if asymptomatic cases tend to resolve quickly, then current estimates of ℛ0 may be over-estimates of the underlying strength (Figure 1B), and asymptomatic cases may be driving a larger fraction of secondary cases than we would expect without accounting for their differences (Figure 1A). The importance of these effects depends on the relative infectiousness of asymptomatic transmission as well as the proportion of incident cases that are asymptomatic (and therefore the intrinsic proportion of asymptomatic transmission z). The biases in the estimates of ℛ0 will necessarily bias estimates of the amount of intervention required to control the epidemic. Note that cases do not have to be completely asymptomatic for our qualitative results to apply. People with mild symptoms unlikely to be diagnosed in a particular time and place (sometimes referred to as subclinical cases) are expected to affect transmission patterns in the same way.
We focus here on the exponential phase, so it is worth noting that the realized proportion of asymptomatic transmission q is time-dependent, varying with dynamic changes in incidence and proportion susceptible. Future work might also consider the ways in which asymptomatic individuals can modulate the catalysis of epidemics in a networked metapopulation [21–23]. Characterizing the role of asymptomatic individuals in driving the persistence of the epidemic will be critical for assessing the post-pandemic outcome [24].
Data Availability
All code is available at https://github.com/mac-theobio/coronavirus_asymptomatic.
Data Availability
All code is available at https://github.com/mac-theobio/ coronavirus_asymptomatic.
Supplementary Materials
A gamma approximation to generation-interval distributions
Assuming that the intrinsic generation-interval distribution for each class (asymptomatic and symptomatic) follows a gamma distribution with mean  and dispersion κc, the average discount of a new infection can be written as:
and dispersion κc, the average discount of a new infection can be written as:
 which shows that the average discount increases with smaller
which shows that the average discount increases with smaller 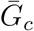 and with larger κc. Then, the odds of the realized proportion of asymptomatic transmission can be written as:
and with larger κc. Then, the odds of the realized proportion of asymptomatic transmission can be written as:
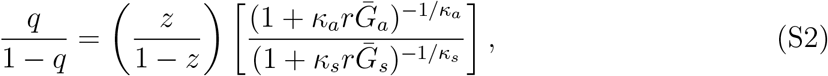 where
where 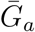 and
and 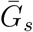 are the mean generation intervals for asymptomatic and symptomatic cases, and κa and κs are the generation-interval dispersions for asymptomatic and symptomatic cases. Finally, the basic reproduction number is calculated by using the Euler-Lotka equation:
are the mean generation intervals for asymptomatic and symptomatic cases, and κa and κs are the generation-interval dispersions for asymptomatic and symptomatic cases. Finally, the basic reproduction number is calculated by using the Euler-Lotka equation:
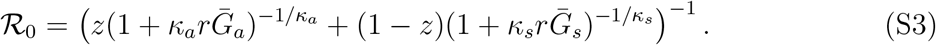
A compartmental model for asymptomatic/symptomatic cases
Consider an SEIR model variant in which an infected individual can be either asymptomatic, Ia, or symptomatic, Is. We note that Ia and Is represent prevalence (i.e., the total number of currently infectious individuals) of asymptomatic and symptomatic individuals; these quantities are different from is and is that we present in the main text, which represent incidence (i.e., the rate at which new cases are generated) of asymptomatic and symptomatic individuals. While both cases can recover, we assume that only symptomatic cases can lead to fatalities, denoted by the D category. In total, the dynamics of susceptibles, exposed, infectious, recovered, and dead are:






Here, βa and βs denote transmission rates, γe denotes the transition from exposed to infectious, p is the fraction of asymptomatic cases that are generated for each exposed individual, 1 − p is the fraction of symptomatic cases that are generated for each exposed individual, γa and γs denote recovery rates, and f denotes the case fatality ratio for symptomatic cases.
Given that the number of infected individuals increase exponentially at rate r initially, the equations for the infectious cases can be rewritten given the ansatz E(t) = ceert, Ia(t) = caert, Is(t) = csert. Then, it follows that

 which implies that
which implies that

This shows that the prevalence of asymptomatic and symptomatic individuals is different from p and 1 − p because prevalence measures the individuals that are currently infectious and does not account for individuals that have already recovered. Finally, the ratio of secondary case production caused by asymptomatic vs. symptomatic individuals during the exponential phase should be
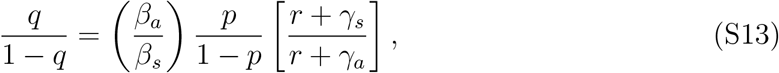 where q is the fraction of new secondary cases caused by asymptomatic individuals.
where q is the fraction of new secondary cases caused by asymptomatic individuals.
The basic reproduction number of this system is:
 where
where


The generation-interval distributions for asymptomatic and symptomatic individuals follow the same functional form as the corresponding generation-interval distribution for a singletype SEIR model since both asymptomatic and symptomatic individuals have exponentially distributed latent and infectious periods [25]:
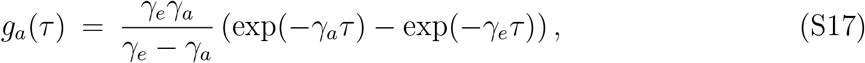
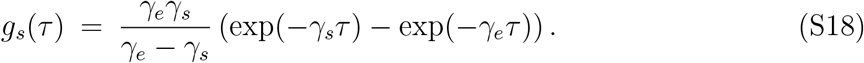
It immediately follows that
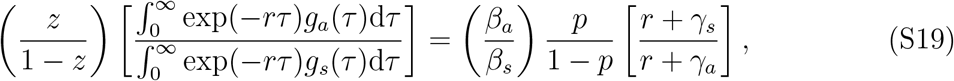 where z = p ℛa/ℛ0 and 1 − z = (1 − p)ℛs/ℛ0 – compare to Eq. (8) in the main text.
where z = p ℛa/ℛ0 and 1 − z = (1 − p)ℛs/ℛ0 – compare to Eq. (8) in the main text.
Supplementary table
Supplementary figures
Differences in the realized and the intrinsic proportions of asymptomatic transmission. See Figure 1 in the main text for figure caption.
Effects of intrinsic proportion of asymptomatic transmission on the realized proportion of asymptomatic transmission and basic reproduction number, given variation in the mean generation interval of asymptomatic cases when generation-interval distributions are narrow. Here, we assume 1/r = 7 days, 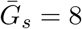 = 8 days, and κs = κa = 0.3. See Figure 1 in the main text for figure caption.
= 8 days, and κs = κa = 0.3. See Figure 1 in the main text for figure caption.
Effects of intrinsic proportion of asymptomatic transmission on the realized proportion of asymptomatic transmission and basic reproduction number, given variation in the mean generation interval of asymptomatic cases when generation-interval distributions are wide. Here, we assume 1/r = 7 days, 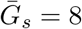 days, and κs = κa = 0.8. See Figure 1 in the main text for figure caption.
days, and κs = κa = 0.8. See Figure 1 in the main text for figure caption.
Effects of intrinsic proportion of asymptomatic transmission on the realized proportion of asymptomatic transmission and basic reproduction number, given variation in the generation-interval dispersion of asymptomatic cases. (A) Wide/narrow generation intervals of asymptomatic cases increase/decrease the relevance of asymptomatic cases, q. (B) Wide/narrow generation intervals of asymptomatic cases decrease/increase the basic reproduction number ℛ0. Solid lines show contours for q and ℛ0 values. Here, we assume 1/r = 7 days, 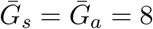 days, and κs = 0.5.
days, and κs = 0.5.
Acknowledgments
The authors thank John Glasser for comments and discussion on the manuscript, particularly on short notice. The authors thank multiple reviewers for their feedback. Research effort by JSW was enabled by support from grants from the Simons Foundation (SCOPE Award ID 329108), the Army Research Office (W911NF1910384), National Institutes of Health (1R01AI46592-01), and National Science Foundation (1806606 and 1829636). JD was supported, in part, by grants from the Canadian Institutes of Health Research.
Footnotes
↵* Electronic address: dushoff{at}mcmaster.ca; URL: https://mac-theobio.github.io/dushoff.html