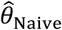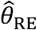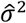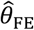ABSTRACT
Host adaptive immune responses may protect against infection or disease when a pathogen is repeatedly encountered. The hazard ratio of infection or disease, given previous infection, is typically sought to estimate the strength of protective immunity. However, variation in individual exposure or susceptibility to infection may introduce frailty bias, whereby a tendency for infections to recur among individuals with greater risk confounds the causal association between previous infection and susceptibility. We introduce a self-matched “case-only” inference method to control for unmeasured individual heterogeneity, making use of negative-control endpoints not attributable to the pathogen of interest. To control for confounding, this method compares event times for endpoints due to the pathogen of interest and negative-control endpoints during counterfactual risk periods, defined according to individuals’ infection history. We derive a standard Mantel-Haenszel (matched) odds ratio conveying the effect of prior infection on time to recurrence. We compare performance of this approach to several proportional hazards modeling frameworks, and estimate statistical power of the proposed strategy under various conditions. In an example application, we use the proposed method to re-estimate naturally-acquired protection against rotavirus gastroenteritis using data from previously-published cohort studies. This self-matched negative-control design may present a flexible alternative to existing approaches for analyzing naturally-acquired immunity, as well as other exposures affecting the distribution of recurrent event times.
INTRODUCTION
Host adaptive immune responses often protect against infection or disease when a pathogen is repeatedly encountered. Vaccines aim to exploit this mechanism of protection by exposing hosts to an attenuated infection, or to immunizing subunits of a pathogen. As such, evidence of protective naturally-acquired immunity provides strong rationale for vaccine development.1 Quantitative estimates of the strength of naturally-acquired protection also inform the interpretation of epidemiologic data, for instance providing a baseline against which vaccine performance can be evaluated.2 These estimates are further sought to parameterize mathematical models of pathogen transmission.3
Naturally-acquired immunity is often estimated via the hazard ratio of infection or disease, comparing counterfactual periods representing person-time at risk in the presence and absence of prior infection.4–10 Thus, inference centers on the distribution of recurrent event times. Unmeasured heterogeneity in individuals’ hazard rates of infection or disease presents a challenge in such analyses, originally termed a problem of “varying liabilities” by Greenwood and Yule11 and subsequently addressed as “accident-proneness”12 or “frailty”.13 The tendency for events to recur among certain individuals must be accounted for in statistical analyses.14 For instance, in studies of naturally-acquired immunity, recurrence of infection or disease among individuals with the greatest susceptibility or exposure to a pathogen, irrespective of previous infection, may bias estimates of naturally-acquired protection.15
This consideration may have relevance to several diseases against which immune responses are thought to generate imperfect protection. Tuberculosis presents a notable example, where despite evidence of protective cell-mediated and humoral immunity,16 several epidemiologic studies have reported higher rates of new-onset infection or disease among persons previously treated successfully for active tuberculosis, as compared to those without history of tuberculosis.17–20 Similar conflict about the consequences of prior infection has arisen in epidemiologic studies of gonorrhea.21,22 In recent analyses of a multi-site pediatric cohort study addressing enteric disease, previous infection predicted higher rates of recurrent infection or disease associated with several pathogens, including Shigella spp., Campylobacter spp., and various diarrheagenic Escherichia coli strains.23 Evidence supporting the feasibility of protective vaccines against many of these pathogens suggests a need to revisit the impacts of naturally-acquired immunity.24–26 Similar causal inference challenges arise in the relationship between chronic inflammation and repeated infection in conditions such as cystic fibrosis,27,28 otitis media,29,30 and environmental enteric dysfunction.31
Formalizing unmeasured heterogeneity as a problem of confounding suggests potential strategies to identify naturally-acquired protection. Terming Y1 and Y2 as primary and recurrent infection or disease outcomes, respectively, and U as the constellation of unmeasured individual factors influencing exposure or susceptibility to a pathogen of interest, a directed acyclic graph (Figure 1) reveals that Y1←U→Y2 may introduce bias into estimation of the causal relationship of interest, Y1→Y2. Conditioning on unmeasured individual factors by comparing observations during counterfactual risk periods from the same individual (Y1←U→Y2) permits unbiased inference of the effect of Y1. This intuition provides the basis for numerous self-matched designs (e.g. case-crossover, case-time control, and self-controlled case series), which have garnered increasing interest in epidemiology in recent years.32
We illustrate a causal framework wherein the effect of previous infection on time to subsequent infection (Y1→Y2) is of interest for analysis. One or more unmeasured confounding factors (U) creates a backdoor path (A) which can be blocked by conditioning on U (B).
In this paper, we present an adaptation of these methods harnessing data from “negative control” events to permit causal inference in the presence of heterogeneous individual frailty. We derive a matched (Mantel-Haenszel) odds ratio (ORMH)33,34 estimator for the hazard ratio of infection or disease, given previous infection. We conduct simulations to compare this approach against alternative methods based on proportional hazards models common in the analysis of longitudinal data, and to assess statistical power under varying conditions. Last, we use the proposed method to reassess protective effects of rotavirus infection in data from previously-published birth-cohort studies.4,5
APPROACH
Self-matched negative control design
Consider an outcome such as acquisition of a pathogen of interest, or onset of disease due to this pathogen (Table 1). The proposed design only includes individuals who experience recurrent episodes of this outcome of interest (case-only). Define Yi and Xi as variables indicating outcome and exposure status for individual i at each observation, with Yi = 1 indicating infection or disease with the pathogen of interest and Yi = 0 indicating a negative-control outcome. Consideration of negative-control observations is of interest for studies involving event-based data capture (e.g. episodes of acute illness), and provides a basis for a competing risks estimation framework as we detail below. Last, let Xi = 1 indicate an individual has previously experienced infection with the pathogen of interest, and with Xi = 0 indicating the individual has no history of infection with the pathogen of interest.
Parameters and definitions.
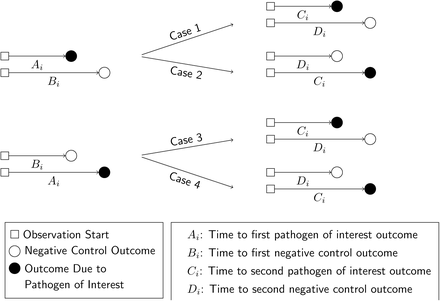
Define Ai-Di as random variables indicating event times for observations of Yi = 1 and Yi = 0, conditioned on Xi, according to the contingency structure presented in Table 2. Ai and Bi are the time to first occurrence of the outcome of interest and the negative control outcome, respectively, for an individual with no history of infection (Xi = 0). Ci and Di are the time to the first occurrence of the outcome of interest and the negative control outcome, respectively, following infection with the pathogen of interest (such that Xi = 1; Figure 2). Here we note that Bi and Di are censored if Ai < Bi and Ci < Di, respectively.
Contingency table for event time distributions, given prior infection.
We illustrate potential outcomes in terms of the sequence of events Ai-Di for a given individual. In cases 1 and 2, we observe Ai < Bi (truncating observation of a negative-control event while Xi = 0). In cases 3 and 4, we observe Bi < Ai, with the negative-control outcome preceding infection with the pathogen of interest. We illustrate the corresponding potential outcomes for Ci and Di, when Xi = 1, in the right-hand side of the figure.
Event time distributions
Define the hazard rate at which an individual i experiences the outcome of interest as λPi, and define θ as the hazard ratio of incidence of this outcome given previous infection (Table 1). Assuming events occur independently any time during the follow up, conditioning λPi and θ, event times are exponentially distributed. Thus, the cumulative probability of experiencing the outcome by time t, for a previously-uninfected individual, is 1 − exp (−λPi t), while the cumulative probability of experiencing the outcome by time t, had the same individual counterfactually been previously infected, is 1 − exp (−θλPi t).
Consider that data are collected from each individual for endpoints besides the primary outcome of interest. Among these, suppose a negative control outcome occurs at a rate λNi for individual i. This rate should be unaffected by individuals’ prior exposure to the pathogen of interest, according to the definition of a negative control in this context.35 Under the same assumptions, the probability of experiencing the negative control outcome by time t, for individual i, is 1 − exp (−λNi t).
Estimating the effect of naturally-acquired immunity
For an individual with no history of previous infection, consider the outcome of interest and the negative-control outcome to be competing risks. The events Ei-Hi may be defined to indicate the relative ordering of event times Ai-Di according to the contingency structure presented in Table 3. Specifically, take Ei = Ai ≤ Bi and Gi = Ci ≤ Di to indicate the outcome of interest precedes the negative-control outcome during the periods with Xi = 0 and Xi = 1, respectively. Define Fi = Bi < Ai and Hi = Di < Ci as complements, where the negative-control outcome precedes infection or disease with the pathogen of interest while Xi = 0 and Xi = 1, respectively.
Contingency table for competing risks, given prior infection.
Under the scenario of exponentially-distributed event times (formulated in Appendices A and B), we have

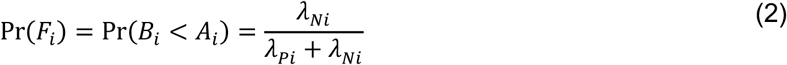
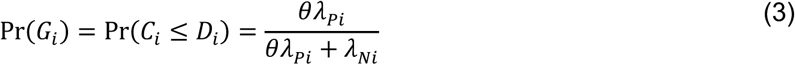
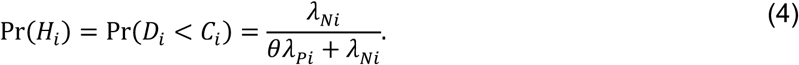
Consider the Mantel-Haenszel odds ratio33,34 constructed from the competing risks of Yi = 1 and Yi = 0, given Xi, matching observations from each individual i:
 such that
such that

Using the above derivations of Pr(Ei) through Pr(Hi),
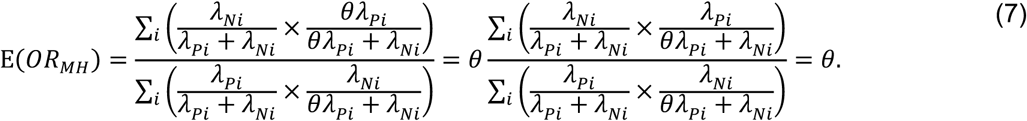
Thus, the ratio of the matched odds for the outcome of interest to precede a negative-control outcome, given an individual’s history of prior infection, provides an unbiased estimate of the effect of previous infection on time to recurrence of the outcome of interest.
Further Considerations
At a design level, self-matched inference reduces or eliminates the potential for bias due to time-invariant factors that individually influence risk.36 However, complications arise when individuals’ risk of experiencing these endpoints differs substantially during the periods before and after individuals experience their first infection with the pathogen of interest.
To consider the implications of such time-varying confounding, define βPi(0) and βPi(1) as multipliers on the rate of infection with the pathogen of interest when Xi = 0 and Xi = 1, respectively, due to all factors other than infection-derived immunity against the pathogen of interest (Table 2). Similarly, define βNi(0)and βNi(1) as multipliers on the rate of the negative-control condition when Xi = 0 and Xi = 1, respectively, due to factors other than prior exposure to the pathogen of interest (Table 4). Here, θβPi (1)/βPi(0) and βNi(1)/βNi(0) are hazard ratios describing the relative incidence rate of the outcome of interest and the negative-control outcome, respectively, in the periods before and after infection with the pathogen of interest.
Contingency table for event time distributions, given prior infection, under the scenario of time-variant confounding.
Here the matched odds ratio is
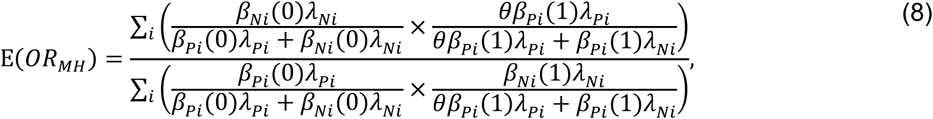 which reduces to θ only when βPi(1)/βPi(0) = βNi(1)/βNi(0) for all individuals. As we address in the Discussion, this circumstance motivates the selection of negative-control outcomes which resemble the outcome of interest in their association with time-varying confounders such as individuals’ age, health status, and sociodemographic exposures.
which reduces to θ only when βPi(1)/βPi(0) = βNi(1)/βNi(0) for all individuals. As we address in the Discussion, this circumstance motivates the selection of negative-control outcomes which resemble the outcome of interest in their association with time-varying confounders such as individuals’ age, health status, and sociodemographic exposures.
We may also consider a scenario where infection with the pathogen of interest alters individuals’ risk of the negative control endpoint, in addition their risk of reinfection or recurrent disease due to the pathogen of interest. Such a circumstance may arise if infection with the pathogen of interest causes individuals to modify risk behaviors that affect multiple outcomes, or confers broad (e.g. multi-pathogen) immunity.37,38
Defining ρ as the outcome-agnostic effect of infection with the pathogen of interest on future outcomes yields the contingency structure of Table 5.
Two-by-two table for event time distributions, given prior infection, in the presence of pathogen-agnostic effects of previous infection.
Here,
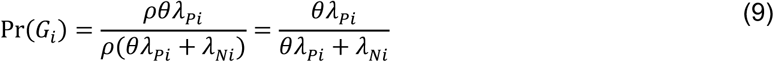
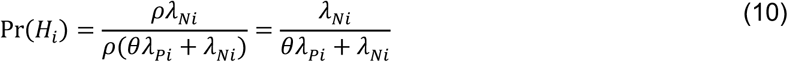 so the parameterization of
so the parameterization of 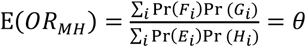 is unchanged. This circumstance is analogous to the more general case where βPi(1)/βPi(0) = βNi(1)/βNi(0)= ρ.
is unchanged. This circumstance is analogous to the more general case where βPi(1)/βPi(0) = βNi(1)/βNi(0)= ρ.
COMPARISON TO COHORT DESIGN USING PROPORTIONAL HAZARDS ANALYSIS
Simulation study
We conducted a simulation study across various underlying distributions of λPi and λNi to test for bias of point estimates under the proposed approach and under alternative methods often used in the analysis of cohort study data (without consideration of negative controls). As comparisons, we considered several proportional hazards models which could be applied to time-to-event data for recurrent observations of the outcome of interest. We considered four approaches to control for differences in hazard rates among individuals with differing exposure or susceptibility to the outcome of interest:
“Naïve” proportional hazards model without inclusion of additional terms to account for differences in event times among individuals. We define the hazard ratio estimated via fitting this model as
 .
.Proportional hazards model accounting for variation in individual frailty via “random effects”. Fitting this model estimates the hazard ratio
 for the effect of previous infection, as well as
for the effect of previous infection, as well as  representing the estimated variance in (log) individual-specific event rates, assumed to represent independent draws from a Normal distribution with mean 0.39,40
representing the estimated variance in (log) individual-specific event rates, assumed to represent independent draws from a Normal distribution with mean 0.39,40Proportional hazards model including Gamma-distributed frailty terms.13 Fitting this model estimates the hazard ratio
 for the effect of previous infection, along with the parameters of the underlying Gamma distribution describing individual-specific frailties.
for the effect of previous infection, along with the parameters of the underlying Gamma distribution describing individual-specific frailties.Proportional hazards model with “fixed effects” for individual subjects. Fitting this model estimates a hazard ratio
 for the effect of previous infection and estimates subject-specific rates of infection (via individual-specific intercepts) which have no pre-specified distributional assumption.
for the effect of previous infection and estimates subject-specific rates of infection (via individual-specific intercepts) which have no pre-specified distributional assumption.
We defined 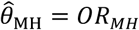 for the proposed analysis strategy of a self-matched, negative control design and considered various distributions for λPi:
for the proposed analysis strategy of a self-matched, negative control design and considered various distributions for λPi:
Truncated Normal distribution (with a pre-specified lower bound at a = 0);
Truncated Cauchy distribution (with a pre-specified lower bound at a = 0);
Uniform distribution;
Gamma distribution;
Mixtures of Gamma distributions.
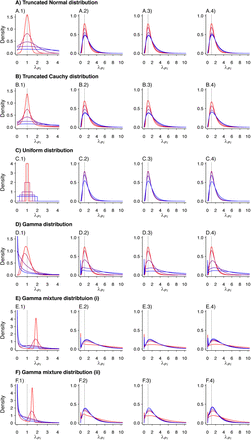
We considered multiple parameterizations of each of these distributions (Table 6), holding the mean rate (or location parameter of the Cauchy distribution) constant at one infection per year across all simulations to determine effects of inter-individual heterogeneity on estimates of θ. We illustrate the distributions in Figure 3. Considering cohorts of 500 individuals, we drew λpi values at random and sampled exponentially-distributed event times of first and second infections for each individual, truncating observations at five years. We repeated simulations 500 times for each θ ∈ {0.01, 0.02, … 0.99}, drawing λPi values independently for each simulation. We used the simulated datasets to estimate 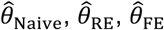 , and
, and  , taking the average of estimates obtained across all 500 iterations to obtain a single point estimate for each parameterization.
, taking the average of estimates obtained across all 500 iterations to obtain a single point estimate for each parameterization.
Event rate distributions applied to simulation study.
Panels are organized to present, in each row, the assumed distribution (column 1), the estimate 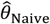 based on a Cox proportional hazards model without any correction for inter-individual heterogeneity (column 2), proportional hazards models employing various frailty frameworks (columns 3-5), and the estimate
based on a Cox proportional hazards model without any correction for inter-individual heterogeneity (column 2), proportional hazards models employing various frailty frameworks (columns 3-5), and the estimate 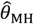 . based on the proposed approach (column 6). One-to-one lines plotted in grey in columns 2-6 indicate where estimates would recover the true value, i.e.
. based on the proposed approach (column 6). One-to-one lines plotted in grey in columns 2-6 indicate where estimates would recover the true value, i.e. 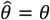 . Horizontal grey lines plotted at
. Horizontal grey lines plotted at 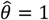 indicate where estimates exceed 1, indicating directionally-misspecified estimates of the causal effect of interest. Values are plotted on a red-to-blue color ramp corresponding to the parameterizations I-V, respectively, in order of least (I; red) to greatest (V; blue) variance as detailed in Table 4. A) Truncated Normal distribution; B) Truncated Cauchy distribution; C) Uniform distribution; D) Gamma distribution; E) Mixture of Gamma distributions (i) with means at 0.125 and 1.875; and F) Mixture of Gamma distributions (ii) with means at 0.5 and 1.5.
indicate where estimates exceed 1, indicating directionally-misspecified estimates of the causal effect of interest. Values are plotted on a red-to-blue color ramp corresponding to the parameterizations I-V, respectively, in order of least (I; red) to greatest (V; blue) variance as detailed in Table 4. A) Truncated Normal distribution; B) Truncated Cauchy distribution; C) Uniform distribution; D) Gamma distribution; E) Mixture of Gamma distributions (i) with means at 0.125 and 1.875; and F) Mixture of Gamma distributions (ii) with means at 0.5 and 1.5.
To compute 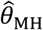 , we drew rates (λNi) and event times for negative control observations from each subject, assuming event times were exponentially-distributed with respect to the underlying rates. To standardize comparisons of
, we drew rates (λNi) and event times for negative control observations from each subject, assuming event times were exponentially-distributed with respect to the underlying rates. To standardize comparisons of 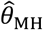 under differing distributions of λPi, we defined λNi = 1 for all i under each simulation.
under differing distributions of λPi, we defined λNi = 1 for all i under each simulation.
To investigate how the different modeling frameworks performed in capturing the distribution of individual-specific hazard rates, we saved estimates of individual-specific fixed effects, random effects, and frailties alongside estimates of 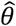 . We fitted a single density kernel to the distribution of individual-specific estimates across 10 simulated cohorts for each true value of θ and underlying distribution of λPi.
. We fitted a single density kernel to the distribution of individual-specific estimates across 10 simulated cohorts for each true value of θ and underlying distribution of λPi.
Results
We plot distributions and estimates under each approach in Figure 3. The naïve hazards ratio tended to overestimate θ, leading to under-estimation of the degree of protection (1 − θ). Bias was minimized as θ approached zero, consistent with a scenario of strong protective immunity. Values of 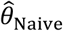 often exceeded 1 in scenarios where θ < 1; in practice, such an estimate would lead to inference that prior infection increases susceptibility to infection or disease due to the pathogen of interest, when in fact prior infection is protective. For all distributions considered, bias in
often exceeded 1 in scenarios where θ < 1; in practice, such an estimate would lead to inference that prior infection increases susceptibility to infection or disease due to the pathogen of interest, when in fact prior infection is protective. For all distributions considered, bias in 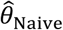 was greatest under parameterizations yielding the highest between-individual variance in λPi.
was greatest under parameterizations yielding the highest between-individual variance in λPi.
Alternative methods performed variably under the differing conditions (Figure 3). Lower degrees of bias were evident in 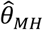 as compared to estimates generated under the other methods assessed. Gamma frailty models and random effects models tended to yield less-biased estimates of θ than
as compared to estimates generated under the other methods assessed. Gamma frailty models and random effects models tended to yield less-biased estimates of θ than 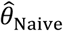 . However, the same direction of bias (resulting in under-estimation of the reduction in susceptibility, or
. However, the same direction of bias (resulting in under-estimation of the reduction in susceptibility, or 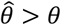 ) was evident with all three of these approaches. Bias was worst when λpi values were drawn from Gamma or Gamma mixture distributions, and tended to increase under distributions with greater variance in λPi, or greater irregularity in the case of Gamma mixture distributions. In contrast, fixed-effects models estimating multipliers on hazard rates for each individual tended to under-estimate θ under most distributions of λPi, although both
) was evident with all three of these approaches. Bias was worst when λpi values were drawn from Gamma or Gamma mixture distributions, and tended to increase under distributions with greater variance in λPi, or greater irregularity in the case of Gamma mixture distributions. In contrast, fixed-effects models estimating multipliers on hazard rates for each individual tended to under-estimate θ under most distributions of λPi, although both 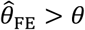 and
and 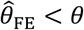 were apparent in simulations using the truncated Cauchy distribution for λPi. For the truncated Normal distribution, bias in
were apparent in simulations using the truncated Cauchy distribution for λPi. For the truncated Normal distribution, bias in 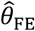 decreased with greater variance in λPi, whereas for the Uniform, Gamma, and Gamma mixture distributions, bias increased with greater variance in λPi.
decreased with greater variance in λPi, whereas for the Uniform, Gamma, and Gamma mixture distributions, bias increased with greater variance in λPi.
Biased estimation of θ occurred in connection with a failure to accurately recover the underlying individual-specific frailty distributions. For each modeling approach, the extent of this misspecification in individual frailties varied over values of θ and distributions of λPi (Supplemental Digital Content, Figures S1-S3).
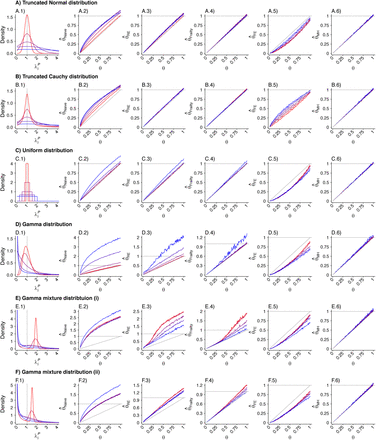
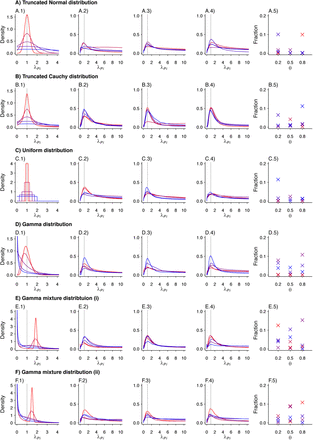
We plot the estimated density kernels for the individual effects estimated by the fixed effects model for each individual in a simulated study. In each row, column 1 is a reproduction of the densities used to produce the individual λPi. Columns 2-4 are the estimated density kernels for θ = 0.2, θ = 0.5, θ = 0.8, respectively. Column 5 shows the proportion of estimates which were over 1000 for each set of parameters. Values are plotted on a red-to-blue color ramp corresponding to the parameterizations I-V, respectively, in order of least (I; red) to greatest (V; blue) variance as detailed in Table 4. A) Truncated Normal distribution; B) Truncated Cauchy distribution; C) Uniform distribution; D) Gamma distribution; E) Mixture of Gamma distributions (i) with means at 0.125 and 1.875; and F) Mixture of Gamma distributions (ii) with means at 0.5 and 1.5.
We plot the estimated density kernels for the individual effects estimated by the random effects model for each individual in a simulated study. In each row, column 1 is a reproduction of the densities used to produce the individual λPi. Columns 2-4 are the estimated density kernels for θ = 0.2, θ = 0.5, θ = 0.8, respectively. Values are plotted on a red-to-blue color ramp corresponding to the parameterizations I-V, respectively, in order of least (I; red) to greatest (V; blue) variance as detailed in Table 4. A) Truncated Normal distribution; B) Truncated Cauchy distribution; C) Uniform distribution; D) Gamma distribution; E) Mixture of Gamma distributions (i) with means at 0.125 and 1.875; and F) Mixture of Gamma distributions (ii) with means at 0.5 and 1.5.
We plot the estimated density kernels for the individual effects estimated by the gamma frailty model for each individual in a simulated study. In each row, column 1 is a reproduction of the densities used to produce the individual λPi. Columns 2-4 are the estimated density kernels for θ = 0.2, θ = 0.5, θ = 0.8, respectively. Values are plotted on a red-to-blue color ramp corresponding to the parameterizations I-V, respectively, in order of least (I; red) to greatest (V; blue) variance as detailed in Table 4. A) Truncated Normal distribution; B) Truncated Cauchy distribution; C) Uniform distribution; D) Gamma distribution; E) Mixture of Gamma distributions (i) with means at 0.125 and 1.875; and F) Mixture of Gamma distributions (ii) with means at 0.5 and 1.5.
SAMPLE SIZE CONSIDERATIONS
Simulation study
To inform applications of the proposed method, we next assessed statistical power under differing conditions. A test statistic (ξMH) has previously been identified for ORMH under the null hypothesis of no difference in risk given exposure.41 For the contingency structure (Table 3) formulated from the terms Ei-Hi (by which we define ORMH), this statistic can be written generally as
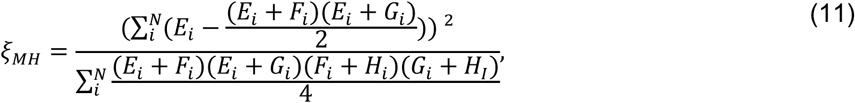 which can then be simplified according to Ei + Fi = 1, Gi + Hi = 1, and Fi + Hi = 2 − Ei − Gi. Thus,
which can then be simplified according to Ei + Fi = 1, Gi + Hi = 1, and Fi + Hi = 2 − Ei − Gi. Thus,
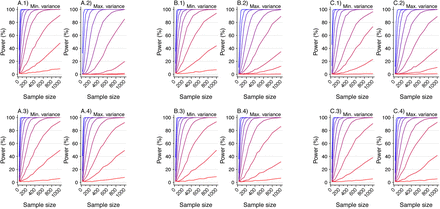
 which is expected to follow a χ6 distribution with one degree of freedom under the null hypothesis. We calculated values of ξMH obtained for cohorts of varying sizes under differing parameterizations of θ, λPi, and λNi. For values of θ ∈ {0.1, 0.2, …, 0.9}, we sampled individual event times Ai-Di for a population of 100,000 individuals whom we subsequently partitioned (without replacement) into 2000 hypothetical study cohorts each of size N=25, 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 700, 800, and 1000. For these analyses, we considered λPi values drawn from truncated Normal, Gamma, and Gamma mixture distributions, under the parameterizations of each of these distributions with greatest and least variance listed in Table 6. We determined statistical power via the proportion of simulated cohorts for which the upper bound of a 95% confidence interval around ORMH would be expected to correctly exclude the null value, i.e. Pr
which is expected to follow a χ6 distribution with one degree of freedom under the null hypothesis. We calculated values of ξMH obtained for cohorts of varying sizes under differing parameterizations of θ, λPi, and λNi. For values of θ ∈ {0.1, 0.2, …, 0.9}, we sampled individual event times Ai-Di for a population of 100,000 individuals whom we subsequently partitioned (without replacement) into 2000 hypothetical study cohorts each of size N=25, 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 700, 800, and 1000. For these analyses, we considered λPi values drawn from truncated Normal, Gamma, and Gamma mixture distributions, under the parameterizations of each of these distributions with greatest and least variance listed in Table 6. We determined statistical power via the proportion of simulated cohorts for which the upper bound of a 95% confidence interval around ORMH would be expected to correctly exclude the null value, i.e. Pr 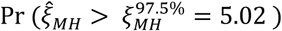 ).
).
To assess how correlation between λPi and λNi could affect the statistical power of estimates, we conducted simulations under two sets of assumptions. Under the first, we considered λNi = 1 for all i (equal to the expected value of λPi under all parameterizations), so that λNi ⊥ λPi; under the second, we defined λNi = λPi, under the assumption that individuals with greater risk of the outcome of interest would also experience higher incidence of the negative control condition. These conditions bound power estimates, corresponding to assuming no correlation and perfect correlation between λNi and λPi, respectively.
Results
We present results of the power analyses in Figure 4. Analyses with as few as 50 subjects had roughly 80% power or greater to estimate θ = 0.1 (corresponding to 90% protection) under all conditions explored; analyses with 500 subjects had 80% power or greater to estimate θ ≤ 0.5 (corresponding to 50% protection or greater) under all conditions. No scenarios revealed 80% or greater power for estimation of θ ≥ 0.8 (corresponding to less than 20% protection), even with 1000 subjects; statistical power for estimation of θ = 0.9 was 10% or lower under nearly all conditions explored.
Each panel presents the statistical power for rejecting the null hypothesis with two-sided p<0.05 under varying conditions. Lines plotted in red to blue correspond to decreasing values of θ: 0.9 (red), 0.8, 0.7, …, 0.1 (blue), corresponding to increasing protection from 10% to 90%. Plots are presented in groups of 4 panels, each corresponding to analyses with values drawn from the following distributions: A) Truncated Normal distribution; B) Gamma distribution; C) Mixture of Gamma distributions with means at 0.125 and 1.875 (as detailed in Table 4). Panels in the top row (A.1, A.2, B.1, B.2, C.1, C.2) represent analyses in which no correlation is assumed between rates of the outcome of interest and negative control outcome (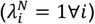 ). Panels in the bottom row (A.3, A.4, B.3, B.4, C.3, C.4) represent analyses in which the correlation between rates of the outcome of interest and the negative control outcome are is maximized (
). Panels in the bottom row (A.3, A.4, B.3, B.4, C.3, C.4) represent analyses in which the correlation between rates of the outcome of interest and the negative control outcome are is maximized (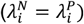 ). Within each grouping, panels on the left-hand side (A.1, A.3, B.1, B.3, C.1, C.3) correspond to distributions with the least variance in individual rates of the outcome of interest (
). Within each grouping, panels on the left-hand side (A.1, A.3, B.1, B.3, C.1, C.3) correspond to distributions with the least variance in individual rates of the outcome of interest (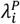 ; i.e., parameterization I in Table 4). Panels on the right-hand side within each grouping (A.2, A.4, B.2, B.4, C.2, C.4) correspond to distributions with the greatest variance in individual rates of the outcome of interest (
; i.e., parameterization I in Table 4). Panels on the right-hand side within each grouping (A.2, A.4, B.2, B.4, C.2, C.4) correspond to distributions with the greatest variance in individual rates of the outcome of interest (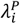 ; i.e., parameterization V in Table 6).
; i.e., parameterization V in Table 6).
For simulations with λNi ⊥ λPi, statistical power was weaker under parameterizations resulting in greater variance in λPi. In contrast, for simulations with λNi = λPi, differences in statistical power were less strongly apparent with increasing variance in λPi. Taken together, these findings suggest statistical power is maximized when negative control endpoints are chosen which tend to occur more commonly among individuals who are at greatest risk of the outcome of interest.
APPLICATION TO ROTAVIRUS BIRTH COHORT DATA
Last, we applied the proposed method to real-world data collected in two birth-cohort studies of rotavirus infection and disease among 200 children in Mexico City, Mexico and 373 children in Vellore, India. These datasets have been described extensively in primary study publications4,5 and subsequent re-analyses.15,42 Similar designs were employed for the studies. Briefly, pregnant mothers were enrolled prior to childbirth, and children were followed from birth to ages 2 years (in Mexico City) and 3 years (in Vellore). Investigators aimed to identify all rotavirus infections through routine testing of asymptomatic stool specimens (collected by field workers at regular home visits) for rotavirus, and by monitoring children for anti-rotavirus seroconversion over serial blood draws at scheduled intervals. Active surveillance was undertaken for all cases of gastroenteritis among children to characterize symptoms and test diarrheal stool specimens for rotavirus.
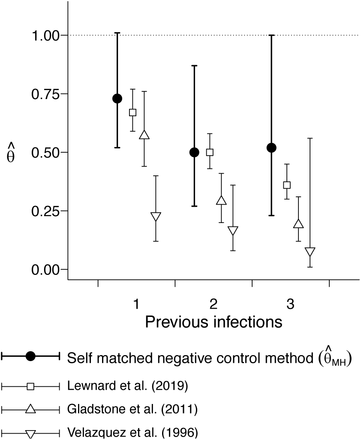
Initial analyses of the datasets led to differing conclusions about the strength of protection against rotavirus gastroenteritis (RVGE). Children in Mexico City were estimated to have experienced 77% (95% confidence interval: 60-88%), 83% (64-92%), and 92% (44-99%) lower rates of RVGE following one, two, and three previous infections, respectively, as compared to zero infections.4 In contrast, children in Vellore, where the rate of rotavirus acquisition was higher, were estimated to have experienced 43% (24-56%), 71% (59-80%), and 81% (69-88%) lower rates of RVGE after one, two, and three previous infections, as compared to zero infections.5 Subsequent analyses of the datasets revealed substantial variation in rates of rotavirus infection and risk of RVGE among individual children, as well as a potential for confounding due to declining risk of RVGE when infections were acquired at older ages, irrespective of previous infection.42 In contrast, model-based analyses accounting for the independent effects of age and previous infection on children’s susceptibility to RVGE estimated that children experienced 33% (23-41%), 50% (42-57%), and 64% (55-70%) lower rates of RVGE after one, two, and three previous infections, respectively, as compared to zero infections.15
We used the proposed self-matched negative control design to re-estimate naturally-acquired protection against RVGE in the cohort datasets. Here, RVGE episodes (acute, new-onset diarrhea with rotavirus detected in the stool) are the outcome of interest and acute, new-onset diarrhea episodes without rotavirus detection as the negative control. We compared the times of RVGE and rotavirus-negative diarrhea episodes from each child beginning from birth, and thereafter following detection of the first, second, and third rotavirus infection (generating confidence intervals via resampling of individual children). This yielded estimates of 27% (–1-48%), 50% (13-73%), and 48% (0-77%) lower rates of RVGE following one, two, and three previous infections, as compared to zero infections (Figure 5). Notwithstanding lower statistical power for the proposed method, these estimates are in agreement with previous findings15 suggesting lower strength of naturally-acquired protection than what was estimated in initial analyses of the birth cohort studies.4,5
We plot point estimates and 95% confidence intervals (lines) for estimates of the hazard ratio of rotavirus gastroenteritis associated with having previously experienced one, two, and three previous infections, versus zero previous infections, estimated via re-analysis of the Mexico City and Vellore rotavirus birth cohort studies.4,5 Analyses include rotavirus-negative diarrhea occurrences as a negative control endpoint.
DISCUSSION
We propose a novel self-matched negative control method for estimating the hazard ratio of time to infection or disease due to a pathogen of interest, given previous infection. Analytically and via simulation, we show this method recovers unbiased estimates under a range of conditions, including when individual incidence rates of the outcome of interest are drawn from highly irregular or skewed distributions. We find these irregular or skewed distributions may lead to bias under proportional hazards models with commonly-used frailty estimation frameworks. Desirably, the proposed approach requires no parametric assumptions other than event-times being exponentially distributed with respect to their underlying, individual-specific rates of occurrence. Beyond infectious disease natural history studies, this approach may have value for assessing the effects of other exposures on recurrent event times.
Our findings provide several practical insights for real-world longitudinal cohort studies. Collecting data on multiple endpoints affords the opportunity to leverage negative-control observations to support causal inference. For studies applying the proposed approach, negative-control endpoints affected by the same risk factors or exposures as the outcome of interest are desirable both to reduce potential risks of confounding due to time-varying factors, and to maximize statistical power based on the correlation between event rates for the outcome of interest and negative-control outcome, λPi and λNi. “Test-negative” control conditions which resemble the outcome of interest, but are not attributable to the same pathogen,43,44 may provide a compelling choice, particularly if their occurrence is predicted by similar risk factors. For instance, shared risk factors are well-documented for rotavirus-positive and rotavirus-negative diarrhea.15,31 Considering respiratory illness, multiple etiologic viruses may share similar seasonal transmission patterns,45 routes of transmission via high-risk contact,46 and associations of disease progression or severity with host comorbidities.47 For sexually-transmitted infections, particular risk behaviors48 differing among individuals or over time could alter risk of any infection, rather than infection with the pathogen of interest alone.25 In the context of real-world cohort studies, test-negative control conditions which are clinically similar to the outcome of interest would likely result in a study visit or other recorded interaction with similar probability. This further supports consideration of inference methods making use of test-positive and test-negative occurrences of a particular clinical syndrome.
In summary, self-matched inference via negative controls may provide a flexible strategy to circumvent bias introduced by variation in individual frailty for analyses of naturally-acquired immunity. Applications to other exposures affecting the distribution of recurrent event times merit consideration, given the possible limitations we identify in existing analysis frameworks.
Data Availability
Code for replication of the analyses is available at github.com/gnorthrup/SelfMatchedNegativeControl.
APPENDIX A COMPETING RISKS
For two competing, independent event times τj and τl occurring at rates rj and rk, the probability for τj to precede τk is
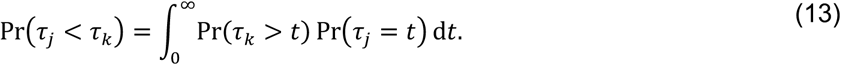
Under the assumption of exponentially-distributed event times,
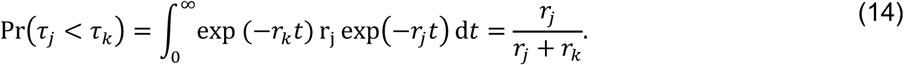
APPENDIX B TRUNCATION OF OBSERVATIONS
The derivation above considers the indefinite integral
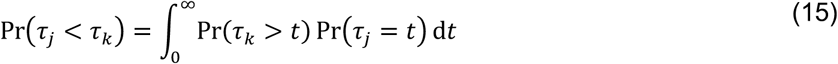
We obtain the same results when considering bounded observations truncated at time δ, more in line with the conduct of real-world studies:
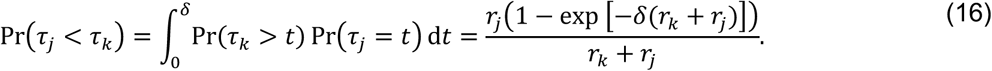
Thus,
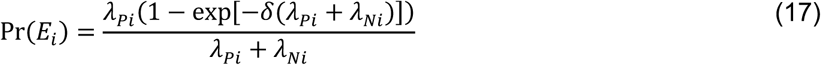
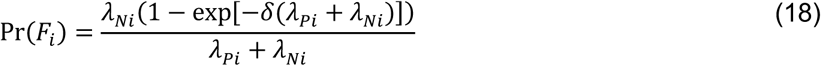
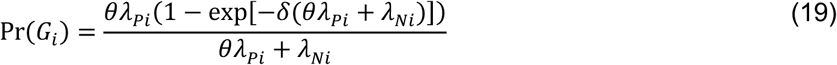
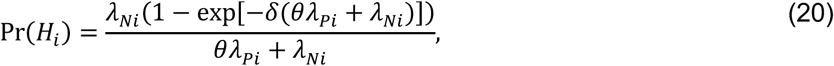 with the additional terms cancelling out in the matched odds ratio formulation:
with the additional terms cancelling out in the matched odds ratio formulation:
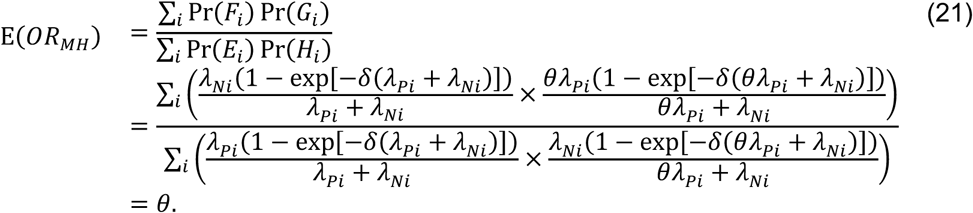
Footnotes
Conflicts of interest: The authors declare no conflicts of interest.
Source of funding: This work was supported by the Dr. E. Dowdle fund from the University of California, Berkeley to JAL.
Materials availability: Code for replication of the analyses is available at github.com/gnorthrup/SelfMatchedNegativeControl.