Transmission Dynamics of Zika Fever: A SEIR Based Model

Abstract

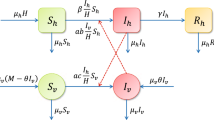
In this paper, a deterministic model is proposed to perform a thorough investigation of the transmission dynamics of Zika fever. Our model, in particular, takes into account the effects of horizontal as well as vertical disease transmission of both humans and vectors. The expression for basic reproductive number $R_0$ is determined in terms of horizontal and vertical disease transmission rates. An in-depth stability analysis of the model is performed, and it is shown, that model is locally asymptotically stable when $R_0 < 1$. In this case, there is a possibility of backward bifurcation in the model. With the assumption that total population is constant, we prove that the disease free state is globally asymptotically stable when $R_0 < 1$. It is also shown that disease strongly uniformly persists when $R_0> 1$ and there exists an endemic equilibrium which is unique if the total population is constant. The endemic state is locally asymptotically stable when $R_0> 1$.

Appendices

Appendix 1: Backward Bifurcation in Model (1)

The model given in the paper has the variables: $S_h, E_h, I_h, R_h, S_v, E_v, I_v$.

Now we redefine these equations by assigning them the following values:

Let $S_h = x_1, E_h= x_2, I_h= x_3, R_h= x_4, S_v= x_5, E_v= x_6, I_v= x_7$. Also let $\hat{f} = [f_1,\ldots ,f_7]$ denote the vector field of the original model in terms of $x_i's$.

Then we have the following model in terms of $x_i's$

$$\begin{aligned} \dfrac{dx_1}{dt}&=f_1= \Pi _h - pB_h x_2-q B_h x_3 - \frac{C_{hv} x_7 x_1}{(x_1 + x_2 + x_3 + x_4)} - \mu _h x_1\\ \dfrac{dx_2}{dt}&=f_2= \frac{C_{hv} x_7 x_1}{(x_1 + x_2 + x_3 + x_4)}+ pB_h x_2 + q B_h x_3 - (\xi + \mu _h) x_2\\ \dfrac{dx_3}{dt}&=f_3= \xi x_2 - (\theta + \delta _{I} + \mu _h) x_3 \\ \dfrac{dx_4}{dt}&=f_4= \theta x_3 - \mu _h x_4 \\ \dfrac{dx_5}{dt}&=f_5= \Pi _v - r B_v x_6 - r B_v x_7 - \frac{C_{hv} x_3 x_5}{(x_1 + x_2 + x_3 + x_4 )} - \mu _v x_5\\ \dfrac{dx_6}{dt}&=f_6= r B_v x_6 + s B_v x_7 + \frac{C_{hv} x_3 x_5}{(x_1 + x_2 + x_3 + x_4 )} - (\sigma +\mu _v) x_6\\ \dfrac{dx_7}{dt}&=f_7= \sigma x_6 - (\mu _v + \delta _v)x_7\\ \end{aligned}$$

Now the disease free equilibrium (DFE) of the system is given by ${\varepsilon _0}$ as follows:

$$\begin{aligned} \varepsilon _0 = \{x_1^*,0,0,0, x_5^*, 0,0\} \end{aligned}$$

Consider the case when $R_0=1$. Take $C_{hv}=C_{hv}^*$ as a bifurcation parameter.

$$\begin{aligned} C_{hv}^*= \sqrt{\dfrac{\Pi _h \mu _v m_1 m_2}{ \xi \sigma \mu _h \Pi _v}}. \end{aligned}$$

The Jacobian of the matrix at the DFE is given by

$$\begin{aligned} J(\varepsilon _0) =\left( \begin{array}{lllllll} -\mu _h &{}\quad -pB_h &{}\quad -qB_h &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -C_{hv}^* \\ 0 &{}\quad -(\xi + \mu _h)+ p B_h &{}\quad q B_h &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{hv}^* \\ 0 &{}\quad \xi &{}\quad -j_1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \theta &{}\quad -\mu _h &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -j_2 &{}\quad 0 &{}\quad -\mu _v &{}\quad -r B_v &{}\quad -sB_v\\ 0 &{}\quad 0 &{}\quad j_2 &{}\quad 0 &{}\quad 0 &{}\quad -j_3+rB_v &{}\quad sB_v\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \sigma &{}\quad -j_4\\ \end{array} \right) \end{aligned}$$

where:

$$\begin{aligned} j_1&=\theta +\delta _I+\mu _h; \qquad j_2=\frac{C_{hv}^* \Pi _v \mu _h}{\Pi _h \mu _v}\\ j_3&=\sigma + \mu _v; \qquad \quad j_4=\mu _v + \delta _v \end{aligned}$$

The above Jacobian matrix of the linearized system has a simple zero eigenvalue (with all other eigenvalues having negative real part). Hence, the Centre Manifold Theory can be used to analyze the dynamics of the system (1). We will use the theorem given by Castillo-Chavez and Song [5].

The Right Eigenvector

The right eigenvector of the Jacobian matrix correspond to zero eigenvalue at $C_{hv}^*$ is given by: w $={w_1,\ldots ,w_7}$, where

$$\begin{aligned} w_1= & {} \left[ \frac{-p B_h j_1 j_3 j_4}{\xi \sigma \mu _h j_2}-\frac{q B_h j_3 j_4 }{\sigma j_2 \mu _h} - \frac{C_{hv}^*}{\mu _h} \right] w_7 , \; w_2=\frac{j_1 j_3 j_4}{\xi \sigma j_2}w_7, \; w_3=\frac{j_3 j_4}{\sigma j_2}w_7\\ w_4= & {} \frac{\theta j_3 j_4}{\mu _h \sigma j_2}w_7 , \; w_5=[-\frac{j_2 j_3 j_4}{\sigma j_2 \mu _v}-\frac{s B_v j_3j_4}{\theta j_2 \mu _h} + \frac{C_{hv}^*}{\mu _h} w_7, \; w_6=\frac{j_4}{\sigma }w_7,\; w_7>0. \end{aligned}$$

The Left Eigenvector

Similarly, the left eigenvector of the Jacobian matrix correspond to zero eigenvalue at $C_{hv}^*$ is given by: v $={v_1,\ldots ,v_7}$, where

$$\begin{aligned} v_1=0, \; v_2=\frac{j_4}{C_{hv}^*}v_7, \; v_3=\frac{q B_h j_4}{j_1 C_{hv}^*}v_7, \; v_4=v_5=0,\; v_6=\frac{j_3}{\sigma }v_7,\;v_7>0. \end{aligned}$$

The Non-zero Derivatives

The value of

$$\begin{aligned} a=\sum _{k,i,j=1}^{7} v_k w_i w_j\frac{\partial ^2 f_k}{\partial x_i x_j}. \end{aligned}$$

So, that

$$\begin{aligned} a= & {} 2w_7^2 v_7 \left( \frac{C_{hv}^* p B_v j_1 j_3^3j_4^2 }{\xi \mu _v \sigma ^3 j_2^2} + \frac{q C_{hv}^* B_v j_3^3 j_4^2}{\mu _v \sigma ^3 j_2^2} + \frac{C_{hv}^{*2}\Pi _v}{\mu _v \Pi _h}\right) -2 w_7^2 v_7 \left( \frac{j_3 j_4^2 (\mu _h j_1+\mu _h \xi +\xi \theta )}{\Pi _h \xi \sigma j_2} \right) \\&-\,2w_7^2 v_7 \left( \frac{C_{hv}^* j_3^3 j_4^2 \Pi _v (j_1 \mu _h+\xi \theta )}{\Pi _h \xi \sigma ^3 j_2^2} \right) -4 w_7^2 v_7 \left( \frac{C_{hv}^* \Pi _v \mu _h^2 j_3^3 j_4^2}{\Pi _h^2 \sigma ^3 j_2^2} \right) -2 \left( \frac{C_{hv}^* j-3^3 j_4^2 \mu _h}{\Pi _h \mu _v \sigma ^3 j_2} \right) \\&+\,\frac{w_7^2v_7q\Pi _hj_4^2\mu _hj_3}{j_1\Pi _h\sigma j_2}\left[ -\frac{s B_v j_3j_4}{\theta j_2\mu _h}+\frac{C_{hv}^*}{\mu _h}\right] . \end{aligned}$$

The value of

$$\begin{aligned} b=\sum _{k,i,j=1}^{7} v_k w_i \frac{\partial ^2 f_k}{\partial x_i C_{hv}^*} \end{aligned}$$

is given by:

$$\begin{aligned} b=\frac{j_4}{C_{hv}^*}v_7 w_7 + \frac{\Pi _v \mu _h j_3^2 j_4}{\mu _v \Pi _h \sigma ^2 j_2} v_7 w_7 \end{aligned}$$

Since b is always positive, backward bifurcation occurs whenever $a>0$.

Appendix 2: Stability of Endemic Steady State

Proof

The proof of Theorem 8 is based on using a Krasnoselskii sub-linearity trick [25, 26].

Rewrite (14) as:

$$\begin{aligned} \dfrac{dE_h}{dt}= & {} \frac{C I_v}{N_h} (N_h - E_h - I_h- R_h) + p B_h E_h + q B_h I_h - (\xi +\mu _h)E_h\nonumber \\ \dfrac{dI_h}{dt}= & {} \xi E_h - (\theta + \mu _h)I_h \nonumber \\ \dfrac{dR_h}{dt}= & {} \theta I_h - \mu _h R_h\\ \dfrac{dE_v}{dt}= & {} \frac{C I_h}{N_h} (N_v - E_v - I_v) + r B_v E_v + s B_v I_v - (\sigma + \mu _v)E_v\nonumber \\ \dfrac{dI_v}{dt}= & {} \sigma E_v - \mu _v I_v.\nonumber \end{aligned}$$

(21)

Linearizing the system (21) around the endemic equilibrium $\displaystyle N_1=(S_h^{\varnothing }, E_h^{\varnothing }, I_h^{\varnothing }, R_h^{\varnothing }, S_v^{\varnothing }, E_v^{\varnothing }, I_v^{\varnothing })$, gives:

$$\begin{aligned} \dfrac{dE_h}{dt}= & {} \left( -\frac{C I_v^{\varnothing }}{N_h} -K_1 + p B_h\right) E_h + \left( -\frac{C I_v^{\varnothing }}{N_h} + q B_h\right) I_h - \frac{C I_v^{\varnothing }}{N_h} R_h + \frac{C S_h^{\varnothing }}{N_h}I_v\nonumber \\ \dfrac{dI_h}{dt}= & {} \xi E_h - (\theta + \mu _h)I_h \nonumber \\ \dfrac{dR_h}{dt}= & {} \theta I_h - \mu _h R_h \\ \dfrac{dE_v}{dt}= & {} \frac{C}{N_h} S_v^{\varnothing }I_h + \left( -\frac{C I_h^{\varnothing }}{N_h}-K_3 + r B_v\right) E_v - \left( -\frac{C I_h^{\varnothing }}{N_h} + s B_v\right) I_v \nonumber \\ \dfrac{dI_v}{dt}= & {} \sigma E_v - \mu _v I_v.\nonumber \end{aligned}$$

(22)

It follows that the Jacobian of the system evaluated at $N_1$ is:

$$\begin{aligned} J(\varepsilon _0) =\left( \begin{array}{lllll} -j_2+pB_h-K_1 &{}\quad -j_2+qB_h &{}\quad -j_2 &{}\quad 0 &{}\quad j_3 \\ \xi &{}\quad -K_2 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \theta &{}\quad -\mu _h &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad j_4 &{}\quad 0 &{}\quad -j_1+rB_v-K_3 &{}\quad -j_1+sB_v\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \sigma &{}\quad -K_4\\ \end{array} \right) \end{aligned}$$

where $\displaystyle j_1=\frac{C I_h^{\varnothing }}{N_h}$, $\displaystyle j_2=\frac{C I_v^{\varnothing }}{N_h}$, $\displaystyle j_3=\frac{C S_h^{\varnothing }}{N_h}$ and $\displaystyle j_4=\frac{C S_v^{\varnothing }}{N_h}.$

Assume that the model (22) has solution of the form

$$\begin{aligned} Z(t) = Ze^{\omega t}; \end{aligned}$$

where $Z=(Z_1, Z_2, Z_3, Z_4, Z_5)$. Substituting Z into (22) gives:

$$\begin{aligned} \omega Z_1= & {} (-j_2+pB_h-K_1)Z_1 + (-j_2 + qB_h)Z_2 -j_2 Z_3 + j_3 Z_5\nonumber \\ \omega Z_2= & {} \xi Z_1 - (\theta _{_I} + \mu _h)Z_2 \nonumber \\ \omega Z_3= & {} \theta _{_I} Z_2 - \mu _h Z_3 \\ \omega Z_4= & {} j_4 Z_2 + (-j_1 + rB_v- K_3)Z_4 + (-j_1 + s B_v)Z_5 \nonumber \\ \omega Z_5= & {} \sigma Z_4 - K_4 Z_5.\nonumber \end{aligned}$$

(23)

We rearranged the above system of equations as follows. First we move the negative terms in the last four equations of (23) to the respective left-hand sides. Secondly, the last four equations are then re-written in terms of $Z_1$. We have

$$\begin{aligned} \omega Z_1= & {} (-j_2+pB_h-K_1)Z_1 + (-j_2 + qB_h)Z_2 -j_2 Z_3 + j_3 Z_5\nonumber \\ Z_2= & {} \frac{\xi Z_1}{(\omega + \theta _{_I} + \mu _{_h})} \nonumber \\ Z_3= & {} \frac{\theta _{_I}(\omega +\theta _{_h}+\mu _{_h}) \xi Z_1 + \theta _{_h}\tau \xi Z_1}{(\omega +\mu _{_h})(\omega + \theta _{_I}+\tau + \mu _{_h})(\omega +\theta _{_h}+\mu _{_h})}\\ Z_4= & {} \frac{(\omega + K_4)j_4 \xi Z_1}{(\omega + K_2)[(\omega + K_4)((\omega + j_1-r\Pi _v+K_3)+(j_1- s B_{_v}))]}\nonumber \\ Z_5= & {} \frac{\sigma (\omega + K_4)j_4 \xi Z_1}{(\omega +K_4)(\omega + K_2)[(\omega + K_4)((\omega + j_1-rB_v+K_3)+(j_1- s B_v))]}.\nonumber \end{aligned}$$

(24)

Substituting the last five equations in the first equation of (23) leads to:

$$\begin{aligned} (1 + F_1(\omega ))Z_1 = (MZ)_1;\nonumber \\ (1 + F_2(\omega ))Z_2 = (MZ)_2;\nonumber \\ (1 + F_3(\omega ))Z_3 = (MZ)_3;\\ (1 + F_4(\omega ))Z_4 = (MZ)_4;\nonumber \\ (1 + F_5(\omega ))Z_5 = (MZ)_5;\nonumber \end{aligned}$$

(25)

where $\displaystyle F_i(\omega )$ for $i=1,\ldots ,5$ are positive functions of parameters and

$$\begin{aligned} M =\left( \begin{array}{lllll} 0 &{}\quad \frac{qB_h}{K_1-pB_h} &{}\quad 0 &{}\quad 0 &{}\quad \frac{C S_h ^{\varnothing }}{N_h(K_1 - pB_h)} \\ \frac{\xi }{K_2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{\theta }{\mu _h}&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{C S_v ^{\varnothing }}{N_h(K_3 - rB_v)} &{}\quad 0 &{}\quad 0 &{}\quad \frac{s B_v}{K_3-rB_v}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sigma }{K_4} &{}\quad 0\\ \end{array} \right) \end{aligned}$$

such that the matrix M has non-negative entries. Define $F(\omega )=min_i|1 + F_i|$. It is easy to verify that the equilibrium point $N_1$ satisfies, $N_1=MN_1.$ The notation $(MZ)_i$ denotes the ith coordinate of the vector MZ. If Z is a solution of (25), then it is possible to find a minimal positive real number r such that $||Z||\le r N_1$ [25, 26]. We want to show that $Re (\omega ) < 0$. Assume, $Re (\omega ) \ge 0$, and consider the following two cases.

Case 1 $\omega = 0.$ In this case (23) is a homogeneous linear system. It is easy to show that the determinant of this system is negative, and it follows that the system (23) has a unique solution, given by $Z = 0$, which correspond to disease free steady state of the model (14).

Case 2 $\displaystyle \omega \ne 0.$ By our assumption in this case $|1+F_i(\omega )|> 1.$ Since r is a minimal positive real number, it follows that

$$\begin{aligned} ||Z||>\frac{r}{F(w)}N_1. \end{aligned}$$

Where $F(\omega )$ is minimal of $|1+F_i(\omega )|.$ From the second equation of (25), we have

$$\begin{aligned} F(w)||Z_2|| \le r I_h^{\varnothing } \end{aligned}$$

which contradicts $||Z||>\frac{r}{F(w)}N_1.$ Hence, $Re (\omega ) < 0$. Thus, all eigenvalues of the characteristic equation associated with the linearized system (14) will have negative real parts. This implies local asymptotical stability of endemic state. $\square$

Appendix 3: Model Parameters

The estimated parameters are presented in Table 3.

Table 3 Mean values of the model parameters with their assigned distributions