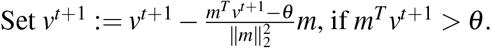ABSTRACT
Massive vaccination is one of the most effective epidemic control measures. Because one’s vaccination decision is shaped by social processes (e.g., socioeconomic sorting and social contagion), the pattern of vaccine uptake tends to show strong social and geographical heterogeneity, such as urban-rural divide and clustering. Yet, little is known to what extent and how the vaccination heterogeneity affects the course of outbreaks. Here, leveraging the unprecedented availability of data and computational models produced during the COVID-19 pandemic, we investigate two network effects—the “hub effect” (hubs in the mobility network usually have higher vaccination rates) and the “homophily effect” (neighboring places tend to have similar vaccination rates). Applying Bayesian deep learning and fine-grained simulations for the U.S., we show that stronger homophily leads to more infections while a stronger hub effect results in fewer cases. Our simulation estimates that these effects have a combined net negative impact on the outcome, increasing the total cases by approximately 10% in the U.S. Inspired by these results, we propose a vaccination campaign strategy that targets a small number of regions to further improve the vaccination rate, which can reduce the number of cases by 20% by only vaccinating an additional 1% of the population according to our simulations. Our results suggest that we must examine the interplay between vaccination patterns and mobility networks beyond the overall vaccination rate, and that the government may need to shift policy focus from overall vaccination rates to geographical vaccination heterogeneity.
Introduction
COVID-19 pandemic is not only a public health challenge but also an immense societal challenge because social processes, such as political polarization and social contagion, significantly impact the course of epidemics1–10. Although the availability of effective vaccines presents a clear solution—reaching the herd immunity11, it is still challenging to predict the course of the pandemic as numerous social factors come into play12–15. These factors include highly unequal vaccine allocation across locations16, heterogeneous vaccine hesitancy across social groups14, and their mixing patterns17,18 in social and mobility networks. Such heterogeneity raises important questions: What are the implications of heterogeneous vaccine uptake across the society? How can we understand and predict the course of the pandemic given the observed patterns of vaccine uptake?
Our study addresses these questions by employing an empirical mobility network dataset and large-scale epidemic simulations with counterfactual vaccination distributions. Departing from the assumption of uniform vaccination and the usage of simplistic models to understand vaccine performance19,20, we employ a data-driven approach to reveal geographic vaccination heterogeneity in the real world by leveraging the availability of fine-grained human mobility data, vaccination data, and census data in the U.S. These rich datasets, along with fine-grained data-driven models21–23, enable us to estimate the outcome of counterfactual vaccination distributions and vaccination campaigns targeting specific regions14,18,24–26.
We propose a network framework to understand the impact of geographic vaccination heterogeneity on COVID-19 cases by focusing on two major network effects. The first network effect is homophily, which describes the phenomenon where similar people tend to cluster, either due to sorting, social contagion, or local regulations3,17,27. In our context, homophily captures the fact that vaccination rates are similar among geographically close or socially connected locations, similarly to other socioeconomic covariates9,27,28. A high level of homophily in vaccination leads to clusters of the unvaccinated, which can trigger localized outbreaks and produce more cases than expected by the overall vaccination rate.
The second network effect is the hub effect: the vaccination rate of central and highly mobile places can have a disproportionate impact on the case count29,30. Given that mobility networks exhibit a high level of degree heterogeneity31, and that the urban population is more likely to be vaccinated in the U.S. due to the current political landscape, the vaccination heterogeneity in the U.S. may potentially reduce the severity of outbreaks. Generally speaking, a well-connected location or a “hub” can either accelerate (if poorly vaccinated) or suppress (if sufficiently vaccinated) the spread of the disease. In many parts of the world, transportation hubs may have a higher vaccination rate32. This could be explained by the positive correlation between the vaccination rate and socioeconomic status33,34.
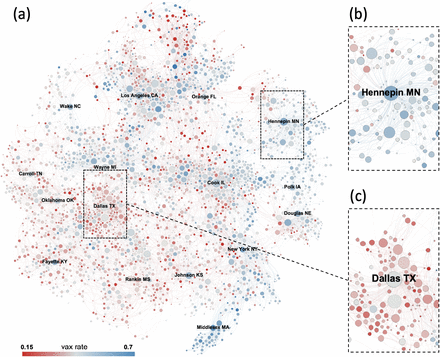
Figure 1 presents the county-level mobility network among U.S. counties (see Materials and Methods for details). Panel (a) is the network for all U.S. counties. The network illustrates strong homophily, shown as localized clusters of the blue and red. For example, we see “blue clusters” for counties close to New York county in NY and Middlesex county in MA, while we observe “red clusters” for counties close to Dallas county in TX and Fayette county in KY. Panels (b) and (c) are the local networks for Hennepin county in MN and Dallas county in TX, respectively. We can observe that these hub counties, which are connected to many other counties, tend to have a higher vaccination rate than their neighboring counties. In the rest of our paper, we investigate the homophily and hub effects at a more fine-grained level of census block groups (CBGs) to maximally leverage the high-resolution mobility dataset.
Illustration of the average vaccination rate in each county and the county-level mobility network backbone (a) among all U.S. counties, (b) for Hennepin county in MN and its adjacent counties, and (c) for Dallas county in TX and its adjacent counties (see Materials and Methods for details). We use the 2019 mobility data to reflect the scenario when all businesses were to fully reopen and vaccination rates are recorded on July 1st, 2021. The mobility network exhibits a high level of degree heterogeneity and strong homophily with respect to COVID-19 vaccination rates. Nodes correspond to counties and are colored according to their vaccination rate, ranging from red (low) to blue (high), and are positioned according to the Fruchterman-Reingold layout35. The node size reflects its network degree. A few major counties are labelled.
Our study consists of three components. First, by designing synthetic networks that exhibit varying degrees of homophily or correlation between network positions and vaccination, we illustrate how these two effects operate in isolation. We then compare them with counterfactual vaccination distributions where we remove or flip the direction of homophily or hub effects (otherwise the same), finding that the homophily effect exacerbates the size of an outbreak, while the hub effect attenuates it.
Second, we repeat the same procedure on the empirical mobility networks and vaccination distribution in the U.S. Because vaccination data is only available at the county level, we leverage additional fine-grained census features and Bayesian deep learning36,37 to infer vaccination rates at the level of the census block groups (CBGs). As discussed in Materials and Methods, our deep learning approach outperforms other state-of-the-art small area estimation methods38. Since our simulations assume the full-reopening scenario, we use pre-pandemic mobility data in 2019. We run simulations with a range of counterfactuals, where the vaccination rates across locations are varied, and show that the observed homophily accounts for at least 17% increase in new COVID-19 infections within 30 days in comparison with counterfactual scenarios without homophily, while the hub effect caused by urban-rural divide reduces the cases compared with the counterfactuals when the correlation between centrality and vaccination rate is eliminated or flipped.
Finally, inspired by these findings, we develop an efficient algorithm to explore the optimal vaccination campaign strategy that focuses on certain locations to further reduce hesitancy and encourage additional vaccinations (given no shortage of vaccines). While it is computationally challenging to run transmission simulations for 200,000 CBGs, our algorithm solves these challenges by using gradient-based optimization on a differentiable surrogate objective. We predict that our proposed campaign strategy can reduce the number of cases by almost 20% with only a 1% increase in overall vaccination rate, as opposed to a 5% reduction with homogeneously distributed vaccination uptake.
Results
Simulation results from two synthetic networks
We begin by employing synthetic mobility networks to study the impact of hubs and homophily on case counts. The goal of this first set of simulations is to isolate the impact of each effect by selectively controlling specific features of synthetic networks. To study the impact of homophily, we construct a clustered network of census block groups (CBGs), where closely connected CBGs have a similar level of vaccination rates and the network is polarized into high and low vaccination regions. Separately, to show the impact of the hub effect, we construct a centralized network with a positive correlation between the network degree of a CBG and its vaccination rate. We then mix these two networks to observe how these two effects jointly affect the outcome. See Materials and Methods for the detailed explanation of how these synthetic networks are constructed.
To measure the impact of homophily or hubs on the severity of outbreaks, we redistribute vaccination over CBGs in the network that removes or flips the homophily or hub effect, but otherwise is identical to the original vaccination distribution including the overall vaccination rate. We can then compare the outcome under a counterfactual and the original vaccination distributions. Differences in the COVID-19 cases would then inform the impact of homophily or hub effects. Throughout the article, we consider four counterfactual vaccine distributions: “reverse”, “exchange”, “shuffle”, and “order.” Their impacts on homophily and the hub effect are illustrated in Table 1 and details are described in Materials and Methods.
Homophily in the networks is largely reduced or removed with “exchange” and “shuffle”, but mostly unchanged by “reverse” and “order”; the hub effect is flipped by “reverse” (i.e., high vaccination CBGs become low vaccination in the counterfactual and vice versa) and removed by “shuffle”, improved by “order”, and mostly unchanged by “exchange”. In all four counterfactual scenarios, we keep the average vaccination rate (population-weighted over CBGs) the same as “original” to prevent any effect from higher or lower overall vaccination rate.
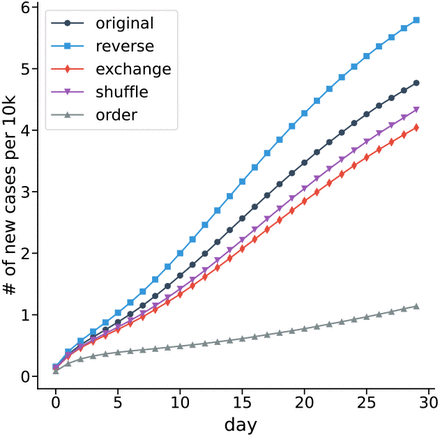
Figure 2 shows the simulated case counts under these counterfactuals, using a pre-assigned proportion of initially infected people (see Materials and Methods for details). The left panel shows any counterfactual that removes the homophily effect (“exchange” or “shuffle”) reduces cases; this confirms our conjecture that stronger homophily increases the number of cases. Since there is no hub effect in this network, “reverse” has the same result as “original”, and introducing the hub effect (“order”) would greatly reduce the cases. The middle panel presents the simulated case counts on the centralized network which has a strong hub effect but no homophily. The main observation is that “shuffle” and “reverse” increase cases because they either eliminate or reverse the direction of the hub effect. Furthermore, since the network already has a perfectly strong hub effect, the “order” does not further improve the outcome. This confirms our assumption that the hub effect attenuates the severity of outbreaks. Since this network does not exhibit homophily, “exchange” does not have any impact.
Simulation results for synthetic networks. (Left) For a network with strong homophily, both “exchange” and “shuffle” remove the homophily, leading to fewer cases. “Reverse” does not affect the homophily, as well as the outcome. “Order” slows down the spread by introducing the the optimal hub effect. (Middle) For a network with strong hub effect, both “reverse” and “shuffle” remove the hub effect, leading to more cases. “Exchange” does not significantly affect the hub effect, nor the number of cases. (Right) A mixture of two networks (clustered and centralized networks) with a tuning parameter λ illustrates how the two effects can be mixed in a single network. Error bars are standard deviations from different runs of simulations.
The right panel shows how new infections change under the counterfactuals for different mixtures of the two synthetic networks. The network includes λ fraction of the edges from the centralized network and 1 − λ fraction of the edges from the clustered network (see Materials and Methods for details). Here the vaccination rate is the weighted average (where the weights are λ and 1 − λ) in the two networks. As λ increases, the case count under the “reverse” counterfactual increases due to a stronger hub effect. Similarly, when λ decreases, the case count under “exchange” decreases due to weaker homophily. These results further verify that homophilous networks with vaccination clustering would have more cases whereas the highly vaccinated hubs decrease them.
Simulation results on the U.S. mobility network
Having illustrated the potential impacts of homophily and hubs, we then examine these effects on the observed U.S. mobility network and vaccination rates. The nationwide mobility network is constructed based on mobile phone users’ home census block group (CBG) and the points of interest (POIs) they visit on an hourly basis (see Materials and Methods for details). We examine the impact of current vaccination patterns when human mobility were to be recovered to pre-pandemic, and thus we use the mobility data from 2019.
Since the vaccination rates are only available at the county level, we extrapolate them to the CBG level using additional CBG-level census demographic and geographic features. We use a graphical model39 and Bayesian neural networks36 to capture the joint distribution between the observed variables (CBG-level census features and county-level vaccination rates) and the hidden variables (CBG-level vaccination rates). We use variational inference37,40 to infer the hidden CBG-level vaccination rates (see Materials and Methods for the description of the algorithm). Similar to the simulations on the synthetic network, we examine the impact of homophily and hub effects on case count using “reverse”, “exchange”, “shuffle”, and “order” counterfactuals described above. Note that here we apply “reverse” counterfactual to each state separately (see Materials and Methods for the rationale).
Figure 3 shows the simulated case counts over 30 days for the original and counterfactual scenarios (see SI for details of the simulation). Compared to the actual vaccine distribution, the “exchange” counterfactual reduces the cases by 17.1%. This result agrees with our conclusion from synthetic networks that homophily in vaccination rate adversely affects the number of new infections. It is also consistent with the high correlation we observe between the vaccination rate of a CBG and that of its neighbors (see SI). The “reverse” counterfactual increases the cases by 22.0%, pointing to the positive impact of high vaccination rates in hubs. Under the “shuffle” counterfactual, which simultaneously eliminates the hub effect and homophily, the number of cases decreases by 11.4%. This result indicates that the homophily effect appears to be the dominant factor. The “order” counterfactual demonstrates the huge potential of further exploiting the hub effect, since assigning the highest vaccination rates to central nodes reduces the case count by 74.5% compared to “original.” In SI, we run separate simulations for each state to investigate how the homophily and hub effect affect the spread within each state, which offers insights into how our results might generalize to other regions or smaller countries.
The number of simulated cases based on the U.S mobility network under various counterfactual scenarios. Error bars are standard deviations of simulations. These results support our hypothesis that the homophily effect harms the outcome while the within-state hub effect improves it. Specifically, by removing homophily, “exchange” reduces the cases. By flipping the hub effect, “reverse” increases the cases. The “order” counterfactual strengthens the hub effect, and greatly reduces the number of cases; “shuffle” eliminates all network effects and leads to a decrease in cases.
Informing effective vaccination campaigns
An effective strategy to increase the vaccination rate is by vaccination campaigns that encourage hesitant individuals to receive vaccination with financial incentives or advertising. Motivated by the strong network effect, we study a hypothetical vaccination campaign strategy that focuses on a small number of CBGs, given aiming for further promoting a fixed number of hesitant individuals to get vaccinated.1 This is a significant computational challenge because we are testing numerous combinations of thousands of CBGs out of over 200,000 CBGs in total. Therefore, we design an algorithm that addresses the computational challenge by using the projected gradient descent41,42 to optimize a computationally feasible surrogate objective. Our proposed approach might be practically feasible to some extent as it could be implemented by concentrating promotions and vaccine availability in the targeted communities. The details of our algorithm and the validation steps are presented in Materials and Methods.
Our objective function implies the uses of both the hub effect and the homophily effect (see Materials and Methods for explanations). To show the effectiveness of the proposed vaccination campaign, we compare it against four baseline policies: untargeted, random targeting, targeting least vaccinated CBGs, and targeting the most central CBGs (see Materials and Methods for details). To guarantee fair comparisons, all policies promote the same number of people (an additional 1% of the U.S. population) to receive the vaccine.
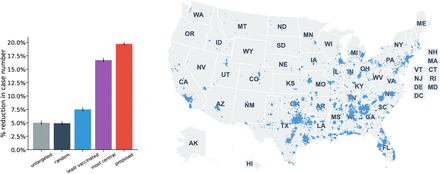
The simulation results are presented in the left panel of Figure 4. First, we find a network externality (or spillover) effect: although all policies are designed to increase the country-wide vaccination by only 1%2, their actual effect is much larger (i.e., at least 4.9%), because vaccines protect not only the vaccinated people, but also the unvaccinated people who may contact the vaccinated. Second, the non-targeting or the random vaccine campaign show the poorest performance among all strategies. Targeting the least vaccinated CBGs achieves slightly better performance, with a 7.5% reduction in the cases. Most importantly, our proposed policy reduces 19.7% of cases, which is three times more than the non-targeting or random targeting strategy. Our proposed campaign also has a significantly better outcome than targeting the most central CBGs, which reduces cases by 16.6%.
(Left) The performance of the four targeting strategies. The y-axis is the reduction compared to the current vaccination distribution (“original”) in the first 30 days. Error bars are standard deviations from different runs of simulations. (Right) The most strongly targeted CBGs whose vaccination rate increases more than 5% under a scenario with our proposed strategy. Each blue dot represents a targeted CBG.
An important question regarding the proposed vaccination campaign is whether it takes advantage of the hub effect (by increasing vaccination rate in central CBGs) or the homophily (by breaking the similarity in clusters of low vaccination). The right panel of Figure 4 presents the map of the targeted CBGs. We observe that our policy primarily targets hub cities and the south (which includes several clusters with low vaccination). 74.9% of the targeted CBGs by the proposed policy overlap with those targeted by the most-central policy. This suggests that an ideal strategy mainly leverages the impact of the hub effect to improve the outcome of the vaccination campaign, echoing the “order” counterfactual result. The proposed strategy also appears to take advantage of the homophily effect, since it reduces the correlation between a CBG’s vaccination rate and its neighborhood average from 0.756 to 0.733 with the 1% increase in the overall vaccination rate. This might explain our further improvement compared with the “most central” targeting strategy.
Discussion
While massive vaccination is crucial to the control of COVID-19, our results show that the geographic heterogeneity of vaccination has a strong impact on the course of the epidemic. Specifically, we show by both synthetically generated networks and real-world mobility networks that homophily can increase case counts whereas hub effects reduce them. We also propose a promising vaccination campaign strategy that would substantially reduce case counts by marginally increasing the vaccination rates in a small number of regions.
Our study may have policy implications beyond the U.S. In addition to the synthetic networks and the U.S. mobility network, we conduct the transmission simulation on the mobility network of each U.S. state, assuming no cross-state mobility, and observe largely similar results. Our conclusions could be generalized to other countries, future mobility trends, or other pandemics such as measles43.
Our results suggest the existence of a huge geographical heterogeneity in the impact of each additional vaccination. By reducing hesitancy and consequently increasing vaccination rates, a small set of locations would have disproportionate impacts on the nationwide outcomes. Thus, the geographical distribution of vaccination may be more informative than the overall vaccination rate in predicting the course of the pandemic. We show that there may be a large, untapped potential to utilize the homophily and the hub effect to improve the effectiveness of the vaccination campaign. Even though it is sometimes suggested that one should focus on the least vaccinated places (in fact, current campaigns are already using this strategy44), our results indicate that this may not be the best strategy for reducing total case counts.
However, our conclusions should be interpreted cautiously. First, our mobility networks are constructed from data provided by SafeGraph, which collects human mobility data from mobile applications. The data may have biases such as over-representing certain demographic groups who use mobile phones more frequently. Moreover, the quality of vaccination data and the predictability of simulation models may also affect the estimated daily case counts. Therefore, we recommend using our results to qualitatively inform policy making, rather than using our exact estimates. If policymakers make decisions based on our approach, the effectiveness of their decision would be further improved if they have higher quality data. Furthermore, any real-world applications based on our study must examine the social implications and ethical concerns. For instance, our proposed campaign strategy may preferentially target certain socio-demographic groups. Note that we focus on campaigns that reduce hesitancy and incentivize vaccination rather than allocating limited extra doses, hence the ethical issues might be less severe than spatial allocation (i.e. providing vaccination only to targeted locations). Nevertheless, we urge that our results should be carefully interpreted and applied by considering diverse social contexts and social inequality. Finally, when performing our proposed vaccination campaign, we should inspect political, legal, and economical feasibility. Those feasibility and ethical issues have to be resolved by the government or specialists.
Materials and Methods
Data collection
The network is constructed using the U.S. mobility from SafeGraph, a company that provides aggregated data collected from mobile applications. All data is anonymized and aggregated by the company so that individual information is not re-identifiable. This dataset has been widely adopted to study human mobility patterns, particularly during the COVID pandemic, such as1,3,23,45–48. Most notably, an epidemic model built on this data—which we adopt in this paper—has shown to be highly predictive of the size of local outbreaks as well as other stylized facts23. SafeGraph receives the location data from “third-party data partners such as mobile application developers, through APIs and other delivery methods and aggregates them.” This data reflects the frequency of mobility between all points of interest (POIs) and the census block groups (CBGs) in the United States. Specifically, the data contains information on the number of people at a CBG who visit a POI on a certain day or in a certain hour. The data also contains the information for each CBG’s area, median dwell times, as well as geo-locations of all CBGs and POIs. In total, there are 214,697 CBGs and 4,310,261 POIs in the U.S. Since this paper aims to measure the counterfactual impact of vaccine distribution if all businesses were to fully reopen, we use the mobility data from U.S. in 2019 prior to the pandemic for our simulation.
We also collected the latest U.S. census data from the SafeGraph database (the complete US Census and American Community Survey data from 2016 to 2019). The data contains the demographic features of each CBG, such as the fractions of each sex, age group, racial and ethnic group, education level, and income level. The Centers for Disease Control and Prevention (CDC)3 provides daily vaccination records on all states except Texas and Hawaii. The Texas Department of State Health Services provides its own data on daily vaccinations4. We joined these data sources and generated the vaccination rate of all U.S. counties (except those in Hawaii) on July 1st, 2021.5
Constructing mobility network of counties or CBGs
We first construct a mobility bipartite network for a given region (country or state), consistent with ref. 23. The edges in the bipartite network are between POIs (denoted by the set 𝒫) and CBGs (denoted by the set 𝒞). The edge weight between a POI p ∈ 𝒫 and a CBG c ∈ 𝒞 corresponds to the number of people who live in CBG c and visit POI p. The bipartite network can vary over time according to the SafeGraph mobility data. However, since our study aims to illustrate the two network effects rather than to provide exact predictions in growth of COVID-19 cases, we aggregate the hourly number of visits in 2019 and construct the bipartite network for each hour given the annual average weights (persons per hour).
The undirected mobility network among CBGs is derived by projecting the aforementioned bipartite graph, considering the areas and dwell times of each POI. In this network, the edges between two CBGs c and c′ is

Here p corresponds to a POI, V (c, p) is the hourly average number of visitors from CBG c at POI p, ap is the area of POI p. dp is the probability of two people visiting the POI p at the same time, derived from the median dwell time at the POI as described in ref.23. This edge weight is consistent with the simulation process proposed by ref.23, as illustrated later in Eq. (2). The edge weight is proportional to the number of people in CBG c who get infected from CBG c′ assuming equal infection rate across all CBGs. The network in Figure 1 is constructed using the same method, but it is at the level of counties instead of CBGs for illustrative purposes. We only retain the top five neighbors of each county with the highest weights (thus making it as a directed graph); and then we convert the directed graph to an undirected one for Fig. 1. We use the full CBG-level network in our simulations.
The synthetic networks
In this section, we explain the construction of the synthetic networks in detail. The construction of networks is consistent with the input in the model of ref. 23, where the basic element is a CBG and individuals are homogeneous among each CBG. For the clustered network, we assume there are 10,000 CBGs each with 10,000 residents. These CBGs are equally divided into 100 clusters, each of which can be considered as a “city.” Similarly, we create 10,000 POIs, which are equally spread out in the 100 clusters. All POIs have identical areas and dwell times. People living in one CBG visit the 100 POIs within the same cluster with a high probability (for each POI with an hourly probability of 40%), but visit the other 9,900 POIs with a small probability (for each POI with an hourly probability of 0.05%). We draw from the Bernoulli distribution to determine whether there exists at least one person from the CBG who visits the POI. To create some heterogeneity in the number of visits, the number of additional visitors follows the Poisson distribution Pois(1). To create the homophily effect, we randomly assign vaccination rates (either 80% or 20%) to clusters. That is, all CBGs in the same cluster have the same vaccination rate, which is either 80% and 20%, which creates a strong contrast of vaccination rates among different groups.
For the centralized network, we also assume there are 10,000 CBGs and 10,000 POIs, with a population of 10,000 in each CBG. However, instead of organizing into clusters of similar vaccination, the CBGs exhibit a high level of variation in their degree centrality. We first generate the random variable Dc for each CBG c, which follows a power distribution (with density function  and 0 < Dc < 1). The CBG is then connected to 100 × Dc (rounded to an integer) randomly selected POIs. In this way, the degree distribution will be skewed with considerable degree heterogeneity among CBGs—a few CBGs will connect to many POIs, thus becoming central, while the majority will connect to only a few POIs. Similar to the clustered network, the number of people who visit each POI from CBG c follows the Poisson distribution Pois(1), which generates a certain level of heterogeneity in the edge weights. To create a positive hub effect, we impose a positive correlation between the degree of the CBG and its vaccination rate. In particular, the vaccination rate of a CBG c is set to be 0.4 + 0.5Dc, thus ensuring that more central CBGs (with higher degree) have higher vaccination rates. Finally, since the degree of each CBG and in particular the set of POIs it is connected to is independent of other CBGs, the network will not exhibit homophily in vaccination.
and 0 < Dc < 1). The CBG is then connected to 100 × Dc (rounded to an integer) randomly selected POIs. In this way, the degree distribution will be skewed with considerable degree heterogeneity among CBGs—a few CBGs will connect to many POIs, thus becoming central, while the majority will connect to only a few POIs. Similar to the clustered network, the number of people who visit each POI from CBG c follows the Poisson distribution Pois(1), which generates a certain level of heterogeneity in the edge weights. To create a positive hub effect, we impose a positive correlation between the degree of the CBG and its vaccination rate. In particular, the vaccination rate of a CBG c is set to be 0.4 + 0.5Dc, thus ensuring that more central CBGs (with higher degree) have higher vaccination rates. Finally, since the degree of each CBG and in particular the set of POIs it is connected to is independent of other CBGs, the network will not exhibit homophily in vaccination.
Finally, hybrid networks (with varying λ) are constructed by mixing the clustered and centralized networks with a parameter λ that controls the composition of the mixture. We first randomly map each CBG in the instance of the clustered network to a CBG in the instance of the centralized network.6 For a given value of λ, an edge between a CBG and a POI in the clustered network is kept with a probability of λ independent of other edges, and similarly an edge from the centralized network is kept with probability of 1 − λ. Thus, a higher value of λ implies a stronger hub effect and a weaker homophily. The vaccination rate of a CBG is the weighted average of the vaccination rates in the centralized network and the clustered network, with weights of λ and 1 − λ respectively.
Inferring CBG-level vaccination rate
County-level vaccination rates are provided by the CDC on a daily basis, while fine-grained CBG-level vaccination rates are unavailable. Because counties cover relatively large, heterogeneous areas and because the epidemic model we use is formulated at the level of CBGs, which offers a much higher resolution than county-level models and predicts the epidemic growth with high accuracy, we estimate the CBG-level vaccination rates from county-level vaccination rates.
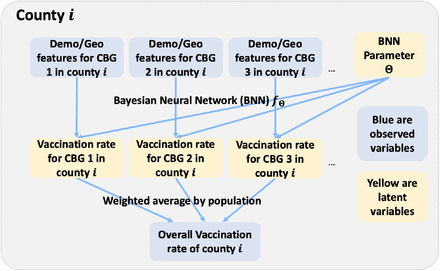
This problem is called “small area estimation”38, where the goal is to use aggregated statistics (such as county-level vaccination rate) and socio-demographic characteristics to infer corresponding statistics at a more fine-grained resolution (such as CBG-level vaccination rate). To enable more accurate inferences, we use demographic and geographic features such as sex, age, race and ethnicity, income level, education level, and geographical coordinates, which are available for all the CBGs. Our assumption is that CBGs with similar features should have similar vaccination rates. This is a missing data imputation problem as illustrated in Fig. 5, where the observed variables are county-level vaccination rates and CBG-level features, while the missing variables are the CBG-level vaccination rates.
A Bayesian latent variable model to impute the CBG-level vaccination rate from the county-level vaccination rate. For each county (indexed by i) we observe the county-level average vaccination rate; for each CBG we observe demographic and geographic features (proportions of different sex, age, racial or ethnic, income, and education groups as well as the geo-locations). The latent variables (which we need to impute) are the vaccination rate for each CBG. We model the mapping from each CBG’s feature to vaccination rate as a Bayesian neural network with unknown parameters Θ. Given the observed variables (blue boxes) we infer the posterior distribution on the latent variables (yellow boxes).
We design a Bayesian model shown in Fig. 5 to impute the missing variables (i.e., the CBG-level vaccination rates). The benefit of the Bayesian approach is that once we define the data generation process, we can compute the Bayesian posterior over the missing variables given the observed variables with standard inference methods37. We define the following data generation process: for each CBG we observe the demographic and geographic features; the features are inputs to a Bayesian neural network36 with unknown parameter Θ, which outputs the vaccination rate of the CBG. Finally, we average the vaccination rates of all CBGs in a county to obtain the overall vaccination rate of that county. Since the posterior inference is approximate, the weighted average of CBG-level vaccination rates in a county does not exactly match the ground truth vaccination rate for that county. Thus, we rescale the inferred vaccination rates to match the ground truth county level vaccination rate. In SI, we present examples of our inferred results. We use the interpolated CBG-level vaccination rates as the input for the downstream simulation tasks.
A major challenge is performance evaluation because no CBG-level ground truth data is available. We thus resort to using county-level ground truth data. We remove 10% of county-level vaccination rate data (i.e., we treat them as unobserved variables in addition to the CBG-level vaccination rates), and infer the posterior vaccination rates for these removed counties. We then compute the mean absolute error (MAE) between the inferred vaccination rate and the ground truth vaccination rate for these counties. For our model, we observe an MAE of 5.23%, while the small area estimation method based on logistic regression (details in SI) has an MAE of 5.82%. This shows that deep neural networks can more accurately capture the non-linear relationships between demographic and geographic features versus the vaccination rates.
Counterfactual vaccine distributions
Here we describe the construction of the counterfactual vaccine distributions in detail:
Original: We use the originally assigned vaccination rates from the inference process discussed above.
Reverse: We “reverse” the vaccination rates. That is, if the original vaccination rate of a CBG c is vc, we assign it to 1 − vc instead. Thus if hubs have high vaccination rates in the original scenario, they will end up with low rates in this counterfactual. The homophily effect is preserved because by reversing all vaccination rates, the network assortativity49 remains the same. For U.S. simulations, we apply the reverse counterfactual to each state separately, which prevents conflating variation in the mobility centrality of different states and helps retain the urban-rural divide in vaccination within states. Also note that due to large differences in vaccination rates across states, conducting the reverse counterfactual across the country may simply capture the effect of heterogeneity in vaccine acceptance among the states with high and low rates, which is not the main point of this paper.
Exchange: We “exchange” the vaccination rates of CBGs with similar mobility centrality scores. Specifically, we first rank all CBGs by their mobility centrality scores (see SI for the definition). We conduct pairwise matching – for each CBG, we find the other with the closest mobility centrality score; and then we exchange the vaccination rates of these two CBGs. In this way, we maintain the correlation between the mobility centrality score and the vaccination rate, while shuffling the vaccination rate distribution such that the homophily effect is reduced. Since the mobility centrality score follows the long tailed distribution, we do not exchange the CBGs with the top 1% mobility centrality scores, which prevents significant impacts from changing the vaccination rates of CBGs with the top 1% mobility centrality.
Shuffle: We also randomly “shuffle” the vaccination rates among CBGs. Therefore, we maintain the average and variance of the vaccination rates while simultaneously eliminating the homophily and hub effect.
Order: We re-”order” the vaccination rates. That is, we first rank the CBGs by mobility centrality score; then for a CBG with a higher mobility centrality score (see SI for the definition), we assign a higher vaccination rate in the original distribution. In this way, we impose the maximum level of the hub effect.
For all counterfactuals, we adjust all the vaccination rates such that the CBG-population-weighted vaccination rate average is the same with the original distribution (by adding and subtracting the differences). We clip vaccination rates in all counterfactuals to range in [0, 1].
Simulating COVID-19 spreading
We extend the model in ref. 23 to simulate the spreading of COVID-19. The model is essentially an SEIR model50, but it is based on the full human mobility data at the level of CBGs and the key parameters in the SEIR model are estimated from the mobility network using machine learning tools. Susceptible individuals (S) first get exposed (E) to the disease with a certain probability after contacting infected people; then exposed people develop symptoms (I, infected) after a period of time; finally, the infected people get recovered or removed (R) after a period of time.
The key difference in our approach is that we also incorporate the vaccination status of individuals in the model using the CBG-level vaccination rate. For example, if a CBG c has a vaccination rate vc, we assume that a fraction vc of individuals in the CBG are “recovered” at time 0. This implies that the efficacy of the vaccination is “perfect” or 100%. Essentially, the number of people in CBG c who newly get exposed (and then infected) at time t from POI p follows a Poisson distribution as shown below:

Here we follow the convention, using 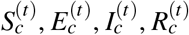 to denote the number of people in CBG c who are susceptible, exposed, infectious, and removed at the time stamp (i.e., hour) t, respectively. Other variables were defined along with Eq. (1). All exposed people will eventually become infectious, and all infectious will eventually become removed.
to denote the number of people in CBG c who are susceptible, exposed, infectious, and removed at the time stamp (i.e., hour) t, respectively. Other variables were defined along with Eq. (1). All exposed people will eventually become infectious, and all infectious will eventually become removed.
Equation 2 also motivates our construction of edge weights for the network. The number of people in CBG i who get infected because of their contact with people from CBG j is proportional to the edge weight we define in Equation 1. This also helps us define the mobility centrality of a CBG (see SI).
Designing the vaccination campaign
Here we explain the selection procedure of targeted CBGs in our proposed vaccination campaign strategy. Let u be the vector of the initial fraction of unvaccinated for each CBG (i.e., one minus the vaccination rate), and v be the increase in the vaccination rate under the campaign. Thus, u − v is the unvaccinated fraction vector after the campaign. Our goal is to find the optimal v* that decreases the case count as much as possible.
The quantity (u − v)TW (u − v) is our objective function, which captures the growth rate of the cases. The intuition is as follows. First, from Eq. (2) we know that the number of people in CBG c who get infected from people in CBG c′ is proportional to 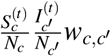 . Under the “perfect” vaccination (i.e., vaccinated people do not get infected), we assume
. Under the “perfect” vaccination (i.e., vaccinated people do not get infected), we assume 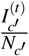 is highly correlated with (or approximately proportional to) the fraction of unvaccinated in c′, which is
is highly correlated with (or approximately proportional to) the fraction of unvaccinated in c′, which is 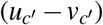 ; and
; and 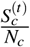 is highly correlated with (approximately proportional to) the unvaccination rate of c, which is (uc − vc). Therefore, the value (uc − vc)wc,c′ (uc′ − vc′) reflects the transmission from CBG c to c′. Using the matrix notation, (u − v)TW (u − v) is approximately proportional to the total transmission for all possible c, c′ pairs, or the number of new cases.
is highly correlated with (approximately proportional to) the unvaccination rate of c, which is (uc − vc). Therefore, the value (uc − vc)wc,c′ (uc′ − vc′) reflects the transmission from CBG c to c′. Using the matrix notation, (u − v)TW (u − v) is approximately proportional to the total transmission for all possible c, c′ pairs, or the number of new cases.
Intuitively, this objective function incorporates both the hub effect and homophily. For the hub effect, the increase in the vaccination rate of a CBG (by vc) reduces the objective function by vc times the mobility centrality score of the CBG (see SI). Therefore, the optimization tends to reduce the vaccination rates of more central CBGs. For the homophily effect, a decrease in a CBG c’s vaccination rate results in the decrease of the objective function that is proportional to wc,c′ (uc′ − vc′) for all other c′ that are connected to c. Therefore, reducing the vaccination rate of one CBG spills over to the adjacent CBGs. The spillover effect is larger if the targeted CBG c is in a cluster of CBGs with similarly low vaccination rates. Thus, the optimization can exploit the homophily in the network by targeting clusters of low vaccination and further reducing the objective function by the spillover effect.
In addition, we impose several feasibility constraints. Specifically, we assume that u − v ≽ 0, which means that no CBG’s unvaccination rate is negative. Also, v ≽ 0, which indicates that vaccination campaign only reduces unvaccination rate and never increases it. We also impose constraints that make the practical implementation of the vaccination campaign possible: specifically, it is difficult to decrease the unvaccination rate of a CBG by a large amount; a 10% increase in the vaccination rate of two CBGs might be much easier than a 20% increase in one CBG. Therefore, we require v ≼ 0.1, i.e., we reduce unvaccination rate of each CBG only up to 10%. Finally, to model finite resources, we limit the total number of vaccine doses to administer by θ, that is ⟨v, m⟩ ≤ θ where m is the population vector of CBGs. For our results, we set θ to 1% of the total population of the country, in other words, the proposed strategy increases the country-wide vaccination rate by at most 1%. Accordingly, the proposed strategy is the solution of the following optimization problem:



More technical details of the optimization approach are included in SI.
Finally, we compare the eventual case counts under the following five campaign policies by running the simulations under the same setting on the U.S. mobility data:
Proposed. It uses the increase in vaccination rate of targeted CBGs proposed by our algorithm. The total number of targeted people is capped at 1%.
Untargeted. It increases the vaccination rates of all CBGs by 1%.
Random. It increases the vaccination rate of randomly chosen CBGs by 10%. This process continues until an additional 1% of the whole population has been vaccinated.
Least vaccinated. It increases the vaccination rate of CBGs with the lowest vaccination rate by 10%. The process of choosing the least vaccinated CBGs continues until an additional 1% of the whole population is targeted.
Most central. It increases the vaccination rate of CBGs with the highest mobility centrality by 10%. The process of choosing the most central CBGs continues until an additional 1% of the whole population is targeted.
Data Availability
All data produced in the present study are available upon reasonable request to the authors
Supplementary Information
Illustrations for synthetic networks
We first provide a simple illustration for our synthetic networks. By “simple”, we mean that we visualize networks of 50 nodes only, although our simulation utilizes 10,000 nodes. The left panel of Fig. S1 presents a centralized network where well-connected hubs tend to have higher vaccination rates. The middle panel illustrates a network of two clusters – one with high and another with low vaccination rates. The right panel presents a network with a mix of edges from both the centralized and the clustered networks. This network has two clusters with different overall vaccination rates. At the same time, it also exhibits centralization with higher vaccination at hubs of each cluster than other non-central nodes of the same cluster.
Simple illustrations of the synthetic centralized network, clustered network, and the mixed network (with λ = 0.5). Blue and red indicate high and or low vaccination rates, respectively. Larger nodes have higher mobility centrality in the network. Nodes are positioned according to the Fruchterman-Reingold layout35.
Details for the parameters in the simulations
Our simulations are based on ref. 23 with modifications to adapt to the goals of our study. For the synthetic networks, we run the simulations over 30 days by setting the initial infection rate to 0.01% and the transmission rate to 0.1. These parameters have no specific meanings and their choice would not change our main conclusions other than the growth rates in Fig. 2. The simulations on the synthetic networks enforce a within-CBG transmission rate of 0 since our focus is on how cross-CBG transmissions affect the eventual case number.
For the U.S. country-level simulation, we set the initial infection rate to 0.1%, the country-wide cross-CBG transiting to ϕ = 1500 (multiplied by a POI’s factor) and within-CBG transmission to 0.005 (these numbers affect the transmission rates). The choice of these values is informed by their estimates in the ten major metro areas studied in ref 23. Marginal changes to these values would not alter our main conclusions significantly.
Ref. 23 employs inferred hourly mobility patterns to conduct simulations which aim to most accurately predict the growth of COVID-19 transmission. By contrast, our study aims to examine how the homophily and hub effects of heterogeneity in vaccination affect the frequency of infections when human mobility returns to the pre-pandemic levels. Thus, the input to our simulations is the hourly average number of visits in 2019 rather than their inferred values above. All our results, including figure 3, are based on the simulations over a period of 30 days.
Mobility centrality
In network science, there are multiple measures for node centrality51. They describe the degree to which each node is central in the network under different contexts. In our study, we employ the weighted degree centrality. Specifically, we use W to denote the weighted adjacency matrix (|𝒞 | ×|𝒞 |). Then, mobility centrality (MC) is defined as

Intuitively, a more mobile and populous CBG, or a CBG connected to many other CBGs (through mutually visited POIs), should have a higher mobility centrality score. There are different ways of defining the edge weights. We choose this edge weight because it directly reflects the extent of transmission between two CBGs, as it corresponds to Eq. (2). Thus, a more mobile CBG is considered more central as it is more vulnerable to contracting the disease. Similarly, there are other valid choices for the centrality score51. However, since our study examines a mobility network of more than 200, 000 CBGs, calculating other centrality measures (such as eigenvector centrality or betweenness centrality) becomes computationally expensive. Nevertheless, as previous work has shown, degree centrality is highly correlated with other centrality measures, specifically eigenvector centrality52. Thus we do not expect the choice of centrality measure to significantly change our conclusions.
Figure S2 presents the mobility centrality maps of California and Texas, the two most populous states in the U.S. As shown in the figure, CBGs that are closer to the large cities (such as Los Angeles and San Francisco in California and Dallas and Houston in Texas) have larger centrality scores. Moreover, CBGs in Texas have larger average mobility scores than those in California, indicating that residents in Texas are on average more mobile than in California.
Measuring homophily in U.S. data
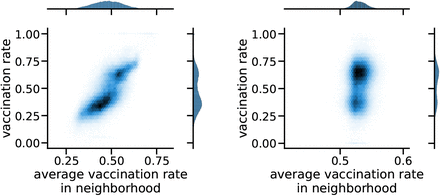
Here, we analyze the correlation between a CBG’s vaccination rate and the weighted average among its neighboring CBGs in the U.S. This analysis is complementary to the simulations discussed in the main text and provides direct evidence on the existence of homophily in the US, yet it does not capture the impact of homophily on the number of infections. Fig. S3 provides an intuitive visualization of the strength of the homophily effect. As shown in the Figure, there is a strong positive correlation between a CBG’s vaccination rate and its neighbors’ weighted average (ρ = 0.756). This strong positive correlation suggests a high level of clustering by vaccination, dense clusters of high and low vaccination CBGs with many connections within and few connections between, which may lead to more infections compared to a uniform vaccine distribution without the homophily effect. Figure S3 also shows this correlation under the “exchange” counterfactual. The correlation is largely reduced, thus confirming the rationale behind the “exchange” procedure which largely reduces the homophily effect.
The mobility centrality maps for the two most populous states in the U.S. The centrality is presented and color coded in log-scale.
Left: The vaccination rate of a CBG versus the average among its neighbors in the network weighted by their mobility centrality under the “original” distribution. Right: The same plot as the one on the left, but under the “exchange” counterfactual.
Measuring hub effect in U.S. data
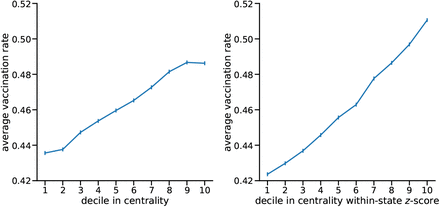
Similar to the previous section, here we present results of a complementary analysis to the simulations which verify the existence of the hub effect. We first divide all CBGs by their mobility centrality51 into deciles, and then plot the average vaccination rate in each decile. Furthermore, to understand the within-state relationship between mobility centrality and the vaccine rate, we plot the vaccination of CBGs versus their within-state centrality z-scores. The country-level and within-state binned scatter plots are presented in Fig. S4.
In the left panel, we see that as centrality in the country network increases by one decile, the average vaccination rate increases by 0.5%. This result suggests a weak but positive correlation between centrality and vaccination. In the right panel, we observe that as within-state centrality increases by one decile, the average vaccination rate increases by 1%. This result suggests that the within-state hub effect is stronger and more significant than the country-level. Thus reversing vaccination rates within states, rather than the whole country, would help us better understand the impact of the hub effect. Moreover, such a “reverse” counterfactual also reflects the urban-rural divide in vaccination that is common in many states.
The average vaccination rates in each decile of the country-wide mobility centrality (left) or the normalized centrality z-score within states (right). Error bars are standard errors of the averages.
Within-state counterfactuals and simulations
The counterfactual analysis in this section is similar to the one presented in the main text, with the exception that the counterfactual procedure is conducted within each state separately, while removing any cross-state mobility from the network. Thus we perform the simulation separately in each of the fifty state and district networks (except Hawaii for which we don’t have vaccination data). The state networks exhibit large variations in their structural properties, which may imply the generality of our results to other regions, especially less populous countries. The results in this section can thus provide extra insights on how geographic heterogeneity in vaccination, especially the homophily and hub effects, affects the overall transmission in different regions.
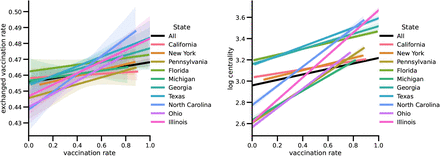
As shown in the upper left panel of Fig. S5, we find that many states exhibit a significant increase in the case count by reversing the vaccination rates, with Kansas, Nebraska, and Oklahoma being the top three states. As for the homophily effect, we find different patterns than the simulation result for the whole country. That is, for many states, the “exchange” counterfactual does not significantly reduce the cases. The state with the most noticeable homophily effect is Virginia, where the “exchange” counterfactual on average reduces the number of new cases by 16.1% and a large discrepancy in vaccination rate is observed between Northeast and Southwest and of Virginia but much less mobility is observed between these two regions.
However, in most other states, the “exchange” counterfactual does not always reduce the case number. We conjecture that this may be due to the following reasons. First, the “exchange” procedure may only succeed in removing the homophily effect in a large region (e.g. the entire U.S.). If we exchange the vaccination rates of CBGs with similar centrality scores in a small region, we may not sufficiently shuffle the vaccination rate such that homophily is largely removed. As shown in the left panel of Fig. S6, there is a very weak correlation between the vaccination rate and the value it is exchanged with for the country-level counterfactual analysis. However, the exchange counterfactual within each state, even in the ten most populous U.S. states, shows a strong correlation between the vaccination rate of a CBG and the value it is exchanged with (right panel). These results imply the limitations of our exchange approach as it potentially retains the homophily effect if applied to small regions. Second, as shown in the right panel, most states show a strong correlation between CBG vaccination rates and their within-state mobility centrality scores, but on the country level such correlation is much weaker. This echoes our results in the synthetic networks: if the hub effect dominates, the exchange counterfactual may not clearly show the homophily effect.
Combining with “shuffle”, we also obtain insights into the effects of the homophily effect. For each state and each counterfactual, we run 25 rounds of simulations and obtain the case numbers. We then generate the “reverse:original” ratio, “exchange:original” ratio, and “shuffle:original” ratio. We treat “shuffle:original” ratio as the dependent variable and “reverse:original” ratio and “exchange:original” as independent variables. With an ordinary least squares model, we find the regression coefficient for the “reverse:original” is 0.328 (p < 0.001) and the regression coefficient for the “exchange:original” is 0.377 (p < 0.001). This result indicates that both the hub effect (“reverse”) and the homophily effect (“exchange”) contribute to the shuffled result. Since “reverse:original” ratios are generally larger than the “exchange:original” ratios, the “shuffle” result (for example the ranks) is consistent with the “reverse” result in the main text.
From the lower right panel, we see that although the current hub effects are shown to be strong from the “reverse” effect, we can still leverage and increase the hub effect to further reduce the case number. For example, we find that by improving the hub effects in states such as New York, Nevada, and Georgia we would observe very large reductions in the case numbers.
The box plots of the ratio of (upper left) “reverse” to “original” (upper right) the ratio of “exchange” to “original”, (lower left) the ratio of “shuffle” to “original”, and (lower right) the ratio of “order” to “original” counterfactuals within each state. States are ranked by the ratio averages.
Details of inferred CBG-level vaccination rates
Here we discuss more details about our Bayesian neural network. We use a three-layer network with ReLU activation. We then assume a Gaussian prior on the parameters of the neural network Θ36. Exact inference over the posterior of a Bayesian neural network is intractable, so we use an approximate inference technique based on dropout37.
(Left) The correlation between the vaccination rate of a CBG and the vaccination rate it is exchanged with in the country-level (all) and state-level (the ten most populous states are presented) simulations. We use linear models to fit the correlations and present the 95% CIs. (Right) The correlation between the vaccination rate of a CBG and the vaccination rate it is exchanged with in the country-level (all) and state-level simulations (the ten most populous states are presented). We use linear models to fit the correlations and present the 95% CIs.
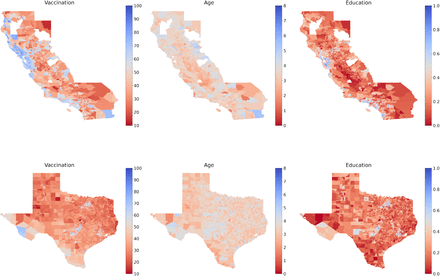
Fig. S7 presents our inferred results of the two most populous states: California and Texas. The left panels of each row present the inferred CBG level vaccination rate. To illustrate how the inferred vaccination rate reflects demographic features, we plot the estimated average age and education level (percentage with Bachelor’s or higher degree) for each CBG as examples. As shown in Figure, the CBGs with higher vaccination rates in general have either a higher average education level or higher average age.
Details of the proposed vaccination strategy
We solve the optimization problem by projected gradient descent41,42 At each step, we take a gradient step to minimize (u − v)TW (u − v). The resulting v might be infeasible, i.e. fail to satisfy the constraints in Eq.(4,5), so we project v back to the feasible set. In particular, to satisfy Eq.(4) we can compute the projection by
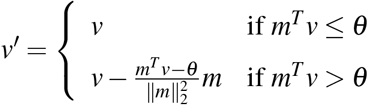
To satisfy Eq. (5) we can compute the projection by

Intuitively, we lower bound vc by 0 and upper bound it by the smaller of 0.1 and uc.
The algorithm must converge with a small enough learning rate based on standard results in optimization theory41,42 (i.e. because each step in the algorithm does not increase the L2 distance to the optimal solution). Upon convergence, the resulting vT is approximately the optimal solution (v*) to the optimalization problem in Eq. (3).
Inferred vaccination rates on the two most populous states. Blue indicates higher vaccination rate (or higher average age or education level) and red indicates low vaccination rate (or higher average age or education level). For comparison, we also plot the average age and education (percentage with college degree). In general, CBGs with either a higher average age or a higher education level have higher vaccination rates. This is consistent with the observation that in general older people have higher vaccination rate (because of earlier access) and better educated people have higher vaccination rate (because of lower hesitancy).
Formally, the algorithm is as follows:
Initialize v0, λ0 = 0, γ0 = 0;
For t = 0, …, T:
vt+1 := vt + η (2W(u−v(t));
Set vt+1 := min(min(max(vt+1,0),0.1),u);
Set
 .
.
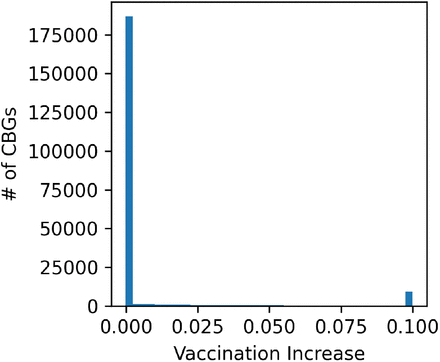
Finally, we plot the histogram of the vaccination rate increases for all the CBGs in Fig. S8.
Histogram of the vaccination rate increases for all the CBGs (0 if untargeted). The histogram is a bi-modal distribution: for the majority of CBGs the vaccination rate increase is 0% (i.e. these CBGs are not included in the vaccination campaign), while for a small proportion of CBGs the vaccination rate increase is 10% (which is the maximum vaccination rate increase that we assume is feasible). Much fewer CBGs are targeted but have an increase smaller than 10%.
Acknowledgements
We thank Ana Bento, Esteban Moro, and Christos Nicolaides for their helpful comments.
Footnotes
↵1 Here we assume vaccination is available to all individuals; the strategy is to encourage hesitant individuals in certain CBGs rather than allocating limited number of doses of vaccines.
↵2 In our data, about half of the population are unvaccinated, so a 1% increase in vaccination rate protects approximately 2% of unvaccinated people.
↵5 The vaccination data from Hawaii is not available and Hawaii is not included in our analysis. Given that their population makes up a tiny fraction and that Hawaii is an island state, we believe that its impact on the country-level outcomes could be marginal or negligible.
↵6 In practice, each CBG has an index from 1 to 10,000 which is independent of its own attributes, and we match on the index.