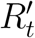1 Abstract
Different combinations of targeted quarantine and broad scale social distancing are equally capable of stemming the transmission of a virus like SARS-CoV-2. Finding the optimal balance between these policies can be operationalized by minimizing the total amount of social isolation needed to achieve a target reproductive number. This results in a risk threshold for triggering quarantine that depends strongly on disease prevalence in a population, suggesting that very different disease control policies should be used at different times or places. Very aggressive quarantine is warranted given low disease prevalence, while populations with a higher base rate of infection should rely more on broad social distancing. Total cost to a society can be greatly reduced given modestly more information about individual risk of infectiousness.
2 Introduction
SARS-CoV-2 transmission can be stemmed either by widespread social distancing, or by effective testing, tracing, and isolation. Social distancing to control the spread of SARS-CoV-2 comes with immense social cost, and is difficult to maintain for long periods. Targeting quarantine to those at higher risk of being infectious has the potential to reduce the indiscriminate harms of social distancing at the whole population level. Here we explore the combination of population-wide social distancing plus targeted quarantine that is best capable of minimizing harms while stemming transmission. This can be operationalized by comparing the harms of different combinations that all achieve the same target value for the effective reproduction number.
Our approach, at the interface of infectious disease epidemiology and economics [1], solves a number of problems previously encountered in that area. It is difficult to decide on an exchange rate between distancing and lives; furthermore, selfish agents may count only the cost to their own life, and not that of others they infect [2]. Difficulties determining an exchange rate lead some to present only idealized curves without a concrete recommendation [3, 4]. Idealized curves can lead to abstract insights, but are of limited use to practical decision-making. Here we make concrete recommendations, e.g. as to exactly how a risk threshold should be set in an exposure notification app.
We avoid the need for an exchange rate between distancing and lives by instead comparing one form of (population-wide, partial) distancing with another form of (targeted, more stringent) distancing. This allows the lowest cost quarantine strategy to be selected without having to monetarize the cost of health outcomes, the latter being held constant in our analysis. The policy optimization problem is thus framed as a minimization of a cost function across different degrees of isolation for different individuals.
Second, prior work tends to integrate across an entire sweep of a pandemic modelled using an SIR approach [5]. This introduces substantial uncertainty relative to our focus on a moment in time. Our focus is informed by a control theory view described in Section 5, regarding how this will generalize to apply over longer timescales.
Third, many models consider decision-making given the possession of instantaneous knowledge [5]. This is problematic given that key indicators such as hospital usage or even positive tests have a marked lag relative to infections. Our approach focuses instead on making optimal use of available, probabilistic information. Past economic approaches to modelling covid treat more stark examples of information, e.g. testing to find out who is infected and should isolate, as opposed to who is exposed to what degree and should quarantine [5, 6]. But quantitative information about individual risk can be obtained from a variety of sources. For example, the risk of infection with SARS-CoV-2 can be estimated based on proximity and duration of contact with a known case, and their estimated infectiousness as a function of timing relative to symptom onset date [7]. Similarly, setting local rather than global shutdown policies, in the light of differences between regions, can lower costs [8].
Our work ultimately describes the value of information, specifically information about who is at high enough risk of being infected to quarantine strictly rather than merely to conform to population-wide distancing measures. Given an individual estimated to be infectious with probability ‘r’, we propose a method for deciding whether to quarantine this individual. We do so by weighing the cost of quarantine against the degree to which indiscriminately applied social distancing would need to be increased to achieve the same reduction in transmission. Our approach informs choice of the lowest cost solution needed to achieve epidemiological targets. In particular, we formalize the intuition that populations with low prevalence should set more strict conditions for quarantine.
3 Optimal Risk Threshold
Consider a population of size P, of which I people are currently both infected and infectious, and S people are susceptible. Let the disease have initial reproduction number R0, and effective reproduction number Rt = R0 ∗ S/P, depending on the fraction of people still susceptible (S/P). Here we define Rt to explicitly exclude interventions such as social distancing or quarantine, because these are the values being optimized. However, Rt is intended to include low cost and fixed cost interventions like mask wearing and improved ventilation.
Population-wide social distancing is parameterized using D, which varies between 0 and 1. A value of 0 indicates normal social contact, 1 indicates complete isolation, and the reproduction number is modeled as proportional to (1− D). Here we assume that the effect of D on transmission is linear, but other variations are explored in section 4. Qi denotes the number of infectious people who are quarantined or isolated and Qn denotes the number of non-infectious people who are quarantined. The effect of targeted quarantine is modeled using 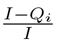 , the fraction of infectious cases who are not successfully quarantined and then isolated. The local effective reproduction number
, the fraction of infectious cases who are not successfully quarantined and then isolated. The local effective reproduction number 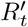 after social distancing and quarantine interventions are applied is given by equation 1.
after social distancing and quarantine interventions are applied is given by equation 1.
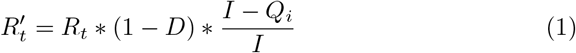
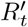 calculates the expected number of onward transmissions per infected case in the general population. Equation 1 is undefined when the number of locally transmitted cases I = 0, and even for low value of I, a different, stochastic treatment warranted - this is discussed in Appendix C. Failing that, equation 1 could be used by assuming a very small expected number of locally transmitted cases I, given uncertainties in importation and subsequent spread.
calculates the expected number of onward transmissions per infected case in the general population. Equation 1 is undefined when the number of locally transmitted cases I = 0, and even for low value of I, a different, stochastic treatment warranted - this is discussed in Appendix C. Failing that, equation 1 could be used by assuming a very small expected number of locally transmitted cases I, given uncertainties in importation and subsequent spread.
The cost of reduced contact for a person is represented by the function f (x), which is assumed to be strictly increasing (from 0 cost with normal contact, to the maximum cost with complete isolation). The exact function is not specified, but in section 4 the resulting risk threshold is shown to have a bounded dependence on its form. For a given level of social distancing and prevalence of quarantine/isolation, the total cost to a population is given by Equation 2, based on (Qi + Qn) people in complete isolation, and (P −Qi −Qn) people with contact reduced by D.

For a target reproductive number, Rtarget, and fixed quarantine quantities, Qi and Qn, the amount of social distancing needed to meet the target can be computed. The solution is given by Equation 3. The value is bounded at 0; if 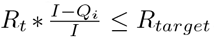 , the target has already been met and no social distancing is required. In many real scenarios it is not possible to adjust D instantaneously or exactly due to changes in quarantine policy. In Appendix D, Equation 3 is shown to be independent of time and control uncertainty if the caseload and control measures are fairly steady over time, as has been the case in many regions for at least some substantial period of time.
, the target has already been met and no social distancing is required. In many real scenarios it is not possible to adjust D instantaneously or exactly due to changes in quarantine policy. In Appendix D, Equation 3 is shown to be independent of time and control uncertainty if the caseload and control measures are fairly steady over time, as has been the case in many regions for at least some substantial period of time.
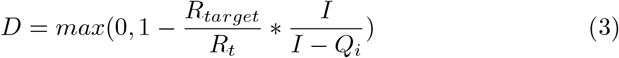
Combining equations 2 and 3, the total cost of a quarantine and distancing scenario is given by J (Qi, Qn) in Equation 4. This equation could be used to compare general quarantine policies using real or simulated data. In the context of comparing classifiers, Qi represents true positives, and Qn represents false positives.

For this work, it is assumed that people under consideration for quarantine have an estimated risk of infectiousness. This could be estimated using proximity and duration of contact with a known case as described in [7]. Or it could be estimated for members of a sub-population like a workplace by rapid testing of a random sample of that sub-population and projecting the proportion positive onto the remainder. If a person with risk of infectiousness, r, were quarantined, Qi would be incremented by 1 with probability r, and Qn would be incremented by 1 with probability 1 − r. Quarantining this person is worthwhile if the expected change in cost given by Equation 5 is less than 0.
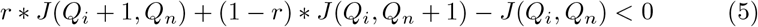
Solving for r, the optimal risk threshold is given by Equation 6.
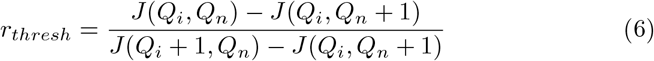
The simplest equation for the cost of isolation is a linear function, f (x) = x. Using this equation in a situation where some social distancing is necessary 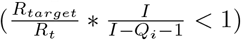 , Equation 6 simplifies to Equation 7.
, Equation 6 simplifies to Equation 7.
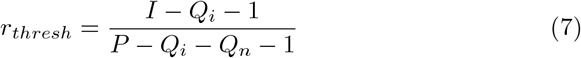
In this simple case, the interpretation of Equation 7 is straightforward and intuitive. The optimal risk threshold for quarantine is based on the disease status within a community. With this simple choice of f (x), the threshold is equal to the disease probability in the community (excluding both those already isolated or quarantined, and the focal individual). This implies that in regions with very low prevalence rates, much stricter quarantine requirements should be used. By doing this, the general population doesn’t need to be as impacted by disease-control measures. In populations with higher prevalence rates there is less benefit to quarantining someone with low risk because they represent a much smaller fraction of the overall disease risk.
4 Sensitivity to Isolation Cost and Benefit Functions
Even the simplest cost and benefit functions can inform an order-of-magnitude risk threshold, which we will see in Section 6 is sufficient for evaluating quarantine policies. Here we discuss several refinements, in part to evaluate sensitivity.
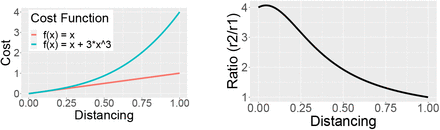
The shape of the isolation cost function, f (x), as the extent of isolation x varies, is unknown. In Appendix A, we show that the deviation from Equation 7 is relatively small for reasonable choices of f (x). In particular, if r1 is computed using f1(x) = x and r2 is computed using any f2(x) that is strictly increasing and concave up, then r2 ≥ r1 and 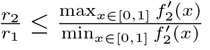 . In practice, the values are often much closer than the upper bound. For example, the difference between optimal risk thresholds for the two cost functions shown in Figure 1 is bounded at a 10-fold difference, and is numerically found to be 4.1-fold.
. In practice, the values are often much closer than the upper bound. For example, the difference between optimal risk thresholds for the two cost functions shown in Figure 1 is bounded at a 10-fold difference, and is numerically found to be 4.1-fold.
The two isolation cost functions (left) differ by a modest ratio in their risk thresholds (r2/r1; right) as a function of population-wide distancing.
Adjustments to Rt or Rtarget shift the amount of broad social distancing needed. For a linear cost function this change has no impact on the risk threshold (except when the target has already been met) because the cost and benefit of the shift exactly cancel out. For concave up cost functions, an increase in Rt/Rtarget will increase the amount of broad-scale social distancing needing, causing a slight decrease in the risk threshold.
Both the cost of isolation and the benefit of isolation can vary among individuals. For example, the cost of isolation is higher for essential workers than for those that can easily work from home, while the benefit of isolation is higher for those whose jobs expose many and/or vulnerable people. Equation 7 can be modified to accommodate knowledge about an individual. If the isolation cost function is a multiple of m more expensive for this person than the general population, and the potential danger to others if they are actually infectious is a multiple of d compared to an average case, then the risk threshold for this person should be modified to rthresh ∗m/d. Note that this approach differs from other suggestions to target isolation directly to the elderly and other high medical risk individuals [4]. We instead recommend increasing the stringency of quarantine among their contacts.
For a given individual, the cost of quarantine is likely to depend more than linearly on its length, due both to logistical and to psychological factors. To accommodate this, the cost of quarantine could be modelled as time-dependent by scaling f (x) ∗ m(t). The benefit of quarantine is not equal for each possible day of quarantine, given a probability distributions for incubation period and quantitative timecourse of infectiousness [7]. Consideration of these two factors will lead shorter recommended quarantine durations, targeted to the most infectious days. Testing individuals in quarantine could further shorten its duration [9].
Equation 3 assumes that the benefits from both social distancing and quarantine are linear. In practice, both are likely somewhere between linear and quadratic [4]. When people seek out places that have variable levels of crowding, benefits are quadratic; when they seek out people who are still willing to meet with them, benefits are linear. The effect of non-linearity is explored in Appendix B.
5 Control of Rt
At the beginning of the COVID-19 pandemic, populations experienced rapid exponential growth, e.g. as high as a 2.75 day doubling time in New York City [10]. Through some combination of top-down control measures and individual behavior modifications, many populations subsequently achieved relatively flat case counts, i.e. an effective R value remarkably close to 1 [11]. Even locations that subsequently lost control of the pandemic have tended to eventually issue stay at home orders leading to exponential decline. Over the very long term, a geometric mean of R not much greater than 1 is inevitable (see Appendix D).
This implies that there is a form of control system (whether intentional or not) using social distancing to regulate transmission rate. A well-functioning control system is one with a negative feedback loop such that the error in achieving a desired outcome feeds in as a correcting input [12]. As case counts rise, contact tracing becomes more difficult, and the subsequent breakdown in quarantine can create a positive feedback loop [13], potentially accelerating the outbreak. Consciously adjusting the risk threshold that triggers quarantine, whether regarding incoming travellers, or risk thresholds in an exposure notification app, contributes to the same positive feedback loop. However, conscious management of this positive feedback loop can manage the process to focus contact tracers’ attention where it can do the most good, in a manner that is under straightforward real-time control.
Control of 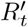 , e.g. to bring it back down to its target given a rise due to seasonal conditions or simply pandemic fatigue, is better exerted through population-wide measures to affect D. Our work shows that this is the socially optimal approach, and indeed if performed adequately, should be accompanied by a perhaps unintuitive relaxing of quarantine. Our formal development so far assumes a perfect control system, and focuses on one-individual perturbations to an equilibrium. It is likely that D will not reliably adjust in a completely timely manner, but a proactive approach can improve the chances of this occurring.
, e.g. to bring it back down to its target given a rise due to seasonal conditions or simply pandemic fatigue, is better exerted through population-wide measures to affect D. Our work shows that this is the socially optimal approach, and indeed if performed adequately, should be accompanied by a perhaps unintuitive relaxing of quarantine. Our formal development so far assumes a perfect control system, and focuses on one-individual perturbations to an equilibrium. It is likely that D will not reliably adjust in a completely timely manner, but a proactive approach can improve the chances of this occurring.
The manner in which control of R′ is achieved matters. Using a simple model, this control system can be explained as a combination of proportional, integral, and derivative control [12]. Derivative control would set social distancing policy based on whether exponential growth has resumed, and if so with what doubling time. This achieves the most effective control, but is unlikely to occur spontaneously, but rather requires government action in response to epidemiological reports not yet of concern to the general population. Spontaneous control by self-interested individuals responding to local conditions would under ideal circumstances follow proportional control, i.e. reflect current case counts. More likely, individuals will respond to the integral of case counts over time, which is the least effective control system, allowing significant fluctuations.
If testing and tracing improves, then less population-wide distancing will be required. This can similarly be recognized as a drop in 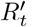 In many cases, this might lead to a reconsideration of Rtarget to a lower level once that seems achievable at lower cost, but otherwise, reductions in social distancing should again ideally be triggered via derivative control.
In many cases, this might lead to a reconsideration of Rtarget to a lower level once that seems achievable at lower cost, but otherwise, reductions in social distancing should again ideally be triggered via derivative control.
6 Examples of application
In a large population with many cases, Equation 6 is closely related to the base rate of infection in the population. When rapid testing is widespread, but only when symptoms are present, as was the case in British Columbia in October 2020, official case counts of around 100/day are a good estimate of symptomatic cases, and asymptomatic and presymptomatic cases can be estimated in proportion. When testing is less adequate, estimating the true number of cases is more complex, involving projections from death rates and/or testing rates, but has been attempted e.g. at [11] or [14]. Assuming another 20 asymptomatic or other undiscovered cases per day in our British Columbia example, each with a 10 day infectious window, yields 200 non-isolated infectious individuals on any given day. In addition, we estimate 4 infectious days per discovered case prior to isolation, yielding another 400 non-isolated infectious individuals on any given day. The base rate of infectiousness, conditional on not having been isolated, is thus of order 600/5,000,000=O(10−4). From Equation 7, a quarantine risk threshold of 10−4 is appropriate, or a little higher if a non-linear cost function is assumed in Equation 6. This implies that quarantine recommendations for entire schools or workplaces may be worthwhile if it is expected to isolate one more infected person than would be achieved via traditional contact tracing.
In contrast, North Dakota in October 2020 had around 400 detected cases per day and perhaps another ∼400 undetected in a population of ∼800,000. This yields ∼5000 undetected infectious individuals on a given day, or a 0.6% base rate and corresponding risk threshold. Several studies have found the secondary attack rate to be on the order of 1/10 - 1/100 [15, 16, 17], so this risk threshold aligns well with standard guidelines for the minimum contact considered close for tracing purposes. We note that 14 day quarantine is more than is needed to put the conditional probability of infectiousness, given lack of symptoms, of a non-household close contact below the base rate [7].
Imported and exported cases introduce complications. Policy is best set for regions that match natural migration, and do not e.g. cut off commuter communities from one another. When imported and exported cases make up only a small fraction of total cases, then subtleties in using case counts to estimate  (discussed in Appendix C) have negligible effects. When local transmissions are abundant enough such that elimination is not a near-term goal, then incoming individuals can therefore be quarantined by comparing their infectiousness risk to rthresh on the basis of base rates of infection in the location they arrived from, plus the risk of travel. These considerations apply e.g. to the need to quarantine following travel from one part of the U.S. to another.
(discussed in Appendix C) have negligible effects. When local transmissions are abundant enough such that elimination is not a near-term goal, then incoming individuals can therefore be quarantined by comparing their infectiousness risk to rthresh on the basis of base rates of infection in the location they arrived from, plus the risk of travel. These considerations apply e.g. to the need to quarantine following travel from one part of the U.S. to another.
Some locations, e.g. British Columbia, have achieved very low levels of local transmission, but the degree of economic connectedness with harder hit locations makes infeasible sufficiently strict quarantine to put the risk from incomers below rthresh as described above [18]. This is because the marginal cost of quarantine applies not just to the quarantined individuals, but to trucking routes and other aspects of the economic system. At this point, some significant expected number of imported cases acts as a forcing function outside the exponential dynamics of 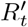 . In this case, it might be better to set a target value for the expected number of cases per day, and then to set Rtarget to achieve this in combination with imported cases.
. In this case, it might be better to set a target value for the expected number of cases per day, and then to set Rtarget to achieve this in combination with imported cases.
If local elimination is achieved, including successfully quarantining all imported cases, then Rtarget can be relaxed up to Rt, removing all social distancing, with huge social gain. The disproportionate benefits warrant careful attention to avoid even a single imported non-quarantined case. How best to achieve this is best quantified by a stochastic model, outside the scope of this paper. Qualitatively, we note that the danger of letting a single case slip through, and hence having to return to social distancing, is higher for larger populations. The harm is magnified by delays in realizing that an outbreak is underway, and hence the extent of harm depends strongly on local surveillance and contact tracing capabilities.
When different regions come under shared political control, importation risk can be controlled at the source rather than the destination. An example is Vietnam in March 2020. Viewed as an entire country instead of as smaller regions, it is optimal to quarantine at a threshold of 1/106. This would motivate quarantining entire cities so that the rest of the country doesn’t have to substantially modify their behaviour. This is similar to the approach Vietnam actually took, with up to 80,000 people in quarantine at a time from regional lockdowns and aggressive contact tracing [19].
7 Discussion
Here we showed that the socially optimal policy is to quarantine an individual if their risk of infectiousness is even mildly above that of the average person in the population who is not under quarantine. How much above depends slightly on the non-linearity of the cost of isolation with the strictness of isolation. In practice, only order of magnitude calculations may be possible in many circumstances, but given that case prevalences vary over orders of magnitudes among populations, our rough calculations are nevertheless instructive. Some tools, like exposure notification apps, have quantitative sensitivities that can be tuned in real time in ways informed by such calculations.
To simplify the optimal trade-off between targeted quarantine and broad social distancing, we have neglected two complications. First, we have based recommendations as to who should quarantine on the assumption that they will do so completely. In reality, quarantined individuals often reduce rather than eliminate non-household contact, let alone all contact. More nuanced messaging regarding the degree of quarantine may be difficult to manage.
Second, how to choose Rtarget is not specified here. In Section 5, we discuss a control theory perspective on the fact that social distancing adjusts to keep the long-term geometric mean of Rt near 1. There are obvious advantages to having it do so against a background of low case counts rather than high case counts. In the shorter term, a separate control problem is whether shorter, sharper action vs. moderate decline with more social freedom achieves the least harm in transitioning between different case prevalences. The choice of Rtarget to control the speed with which case numbers are brought to low levels must also place a value on illness and death in comparison with social restrictions, a difficult problem. We note that in practice, compliance with transmission control measures such as size limits to gathering, compulsory masking etc. can be hard to predict, and hence the degree of top-down control is limited. This underlies our decision in this manuscript to focus on marginal costs given prevailing policy and behaviors.
The total cost of social distancing could be reduced if we issued immunity passports. In Equation 2, the total number of people who need to socially distance could be reduced from P − Qi − Qn to S − Qi − Qn, which becomes substantial when S < P. The problem with immunity passports is that they set up an adverse incentive in favor of contracting SARS-CoV-2, especially for young and healthy individuals, where the risks from illness are outweighed by the subsequent restoration of freedom from social distancing constraints. To avoid creating such an adverse incentive, it may be necessary to continue to enforce some social distancing requirements even on those who are likely immune. However, with increasing vaccine availability, the benefits from immunity passports will rise and the adverse incentive to get infected gets converted into a socially aligned incentive to get vaccinated.
In many countries, compliance not just with social distancing, but also with quarantine has been low. This is to be expected, given the uncompensated cost of quarantine to individuals, who are currently asked (or in cases coerced) to sacrifice for the public good. We advocate that governments align incentives, by guaranteeing e.g. 150% the individual’s normal daily income. This approach can also be used to assign a dollar value to quarantine, on the order of USD$150 per day of complete quarantine. This is the implied utility sacrificed by either total quarantine or equivalent social distancing D. I.e., this is what one would need to pay people in order to incentivize their compliance, i.e. to achieve neutrality among preferences.
Cost as a function of the degree of social distancing should be interpreted as total cost to society, i.e. both individual preferences for one day of total quarantine vs. two days of 50%, and incidental consequences and expenses. Redistributive payments move this cost from the quarantined individuals to the taxpayer. Part of the curvature of the cost function comes from the need for room and board, so that quarantined individuals do not put their household members at risk. Placing a dollar value on the marginal cost of quarantine is instructive regarding the value of information about risk of infectiousness. With better risk resolution, fewer people need to be quarantined in order to achieve a target level of transmission reduction.
As proof as principle of the value of information, we simulate a range of encounters using the COVID Tuner risk score configuration tool [20], following a 3D grid with distance distributed uniformly between 0 and 5 meters, durations uniformly between 5 and 30 minutes, and date relative to symptom onset date uniformly between −10 days and +10 days. This tool, on the basis of the current public health definition of close contact (2 metres for 15 minutes from day −2 to day +9) uses an implicit risk threshold of 0.002. We simulate the Swiss, Irish, and Arizonan configurations included in this tool, plus a “baseline” configuration that is equivalent to the Arizonan configuration but with only two rather than 6 non-zero levels of infectiousness. The Swiss and Irish configurations use only one non-zero level of infectiousness.
We assume that the cost of quarantine is $150 per day, and that the average quarantine is 10 days long. This gives an expected cost of quarantine of $1500 per individual that a particular configuration succeeds in getting to quarantine. At the margin, this indicates the value that society implicitly places, i.e. that removing a 0.002 risk is worth $1500. The benefit of quarantine is calculated in terms of “excess risk” above 0.002 having a value where each 0.002 of excess is worth $1500.
Net benefit was calculated for the specific scenario of a population of 10 million, 2% of whom test positive over the time period of interest. We assume that 20% use the app, of whom 50% enter their diagnosis into the app, thus notifying 20% of contacts that the app scores as above threshold risk, who go on to infect half as many people as they would were they not contacted. We assume the cost of quarantine is similarly only half what it would be given complete compliance. We assume that each has 30 contacts following the distribution described above. Net benefit comes out to $6.1 million for the Irish app, $6.2 million for the Swiss app, $11.4 million for the baseline app and $14.7 million for the Arizonan app. The differences between these figures illustrates the importance of infectiousness information - unfortunately, version 2 of the Google/Apple exposure notification system restricts the number of non-zero levels of infectiousness down to two.
We note that the value of an exposure notification app would be dramatically higher if, instead of a blanket 14 day quarantine duration, a shorter quarantine, targeted to the days of greatest risk, were used [7]. Further gains would come from using negative test results to shorten quarantine. We have shown here how to use information about expected infectiousness to recommend quarantine in a socially optimal way, by treating risk consistently, and quarantining those above a threshold. We further provide order of magnitude methods to choose the optimal threshold. The more information we have about risk, the more that quarantine policy creates the conditions for a return to more normal life.
Data Availability
NA
9 Competing Interests
Joanna Masel consults for WeHealth, distributor of the Covid Watch app to Arizona. James Petrie is likely to soon sign a contract giving him an equity interest in WeHealth.
8 Acknowledgements
James Petrie acknowledges support from the Ontario Graduate Scholarship and thanks his advisor, Prof. Stephen Vavasis, for giving him the freedom to work on this research project. We thank Kevin Murphy at Google for access to his COVID Tuner risk score configuration tool, and the entire WeHealth team for their ethical commitment to maximizing benefits while minimizing harm, including via the recommendations of this paper.
Appendices
A. Cost Function Dependence
Consider the situation where r1 is calculated using f1(x) = x, and r2 is calculated using f2(x), where f2(x) is strictly increasing, concave up, and differen-tiable. For both of these calculations, define 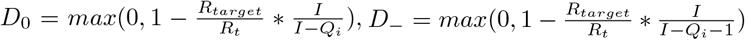 , and Q = Qi + Qn. The two risk thresholds are then given by equation 9 and 10.
, and Q = Qi + Qn. The two risk thresholds are then given by equation 9 and 10.
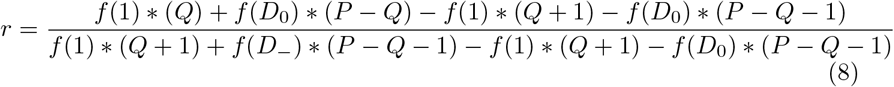
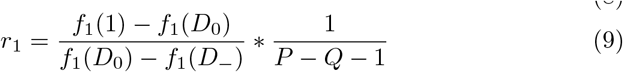
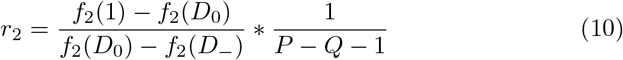
Substituting f1(x) = x, and taking the ratio of the two thresholds gives Equation 11. Since 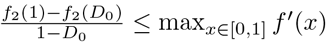 , and
, and 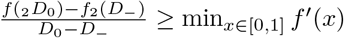 , then Equation 12 gives a bound on the ratio of the two thresholds. If f2(x) is concave up (indicating that additional isolation is more costly), then
, then Equation 12 gives a bound on the ratio of the two thresholds. If f2(x) is concave up (indicating that additional isolation is more costly), then 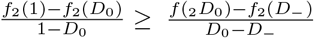 , and therefore r2 ≥ r1.
, and therefore r2 ≥ r1.


B. Matching Function Dependence
The effect of social distancing on transmission reduction was previously assumed to be linear. Here we show that for α ∈ [1, 2] the risk threshold computed using 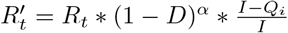 is approximately a multiple of α greater than whenα = 1.
is approximately a multiple of α greater than whenα = 1.
Define 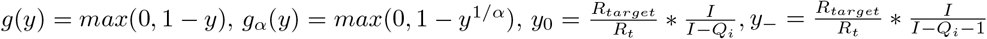
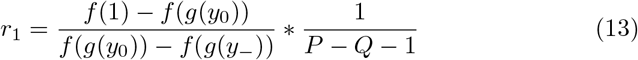
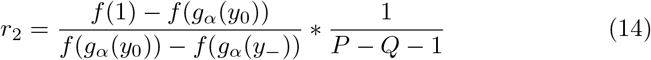

Assuming y0 < 1, y− < 1 (some social distancing necessary)
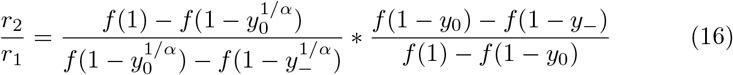
Setting the cost function f (x) = x

Define Δy = y− − y0

Using the Taylor expansion to replace  with
with  :
:


C. Imported Cases and Stochasticity
For regions where imported cases make up a significant fraction of total cases, policy makers should consider the modified dynamics when choosing Rtarget. Imported cases act as a forcing term, with the number of cases at a future timepoint being the sum of locally obtained infections and imported infections.
The mechanics of choosing a risk threshold do not change, but it is important to highlight that Rtarget only determines a portion of future cases. A complete solution must also consider the effect of border policies.
When the total number of cases is small, e.g. in a region with excellent local control for which imported cases are the primary concern, discrete and stochastic effects become important.
Quantitative models of tiny case count scenarios are challenging, because of stochasticity in the length of time needed to return to elimination, combined with curvature in the harms of shutdown as a function of its length. This is further exacerbated by superspreader dynamics, i.e. the low over-dispersion parameter [21]. Modelling the number of secondary cases with a negative binomial distribution with over-dispersion 0.1 and mean 2.5 yields a variance of 65. In locations not aiming for local elimination, stochasticity averages out over time, and expected values can be used. When local elimination is being attempted, it would be useful to make use of discrete, stochastic models when choosing Rtarget, e.g. to calculate the probability distribution of time to elimination and the expected damage from shutdowns of different severity. With the choice of Rtarget set, the previous arguments mostly still hold (although some consideration may be given to the difference in variance in transmissions based on broad vs. targeted distancing).
If local elimination has already been achieved, then a still more complicated case is to consider the risk of an outbreak from an imported case, the time delay and growth in the outbreak before it is noticed, and the subsequent shutdowns needed to re-achieve local elimination and thus relax general social distancing. It is likely that the considerable costs of such an outbreak warrant strict quarantine for incoming individuals. A robust testing and contact tracing system capable of quickly containing any new outbreak is also key.
D. Long-term 
In Section 3, the relationship between broad social distancing and targeted quarantine/isolation was presented with Rtarget constrained at an instant in time. In this section, we show that the same relationship holds when averaged over time, even including stochastic effects, time delays, and uncertainty about system state. To make this argument, we assume that for a certain region and time frame, the virus is neither eliminated nor infects the entire population, and that control measures are relatively stable. In this situation, the product of 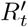 over time must be within a few orders of magnitude of 1, so we assume that
over time must be within a few orders of magnitude of 1, so we assume that  . N denotes the number of serial intervals considered and Dinf (t) gives the number of daily infections at a certain time. Replacing
. N denotes the number of serial intervals considered and Dinf (t) gives the number of daily infections at a certain time. Replacing 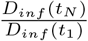 with the product of R over time gives:
with the product of R over time gives:
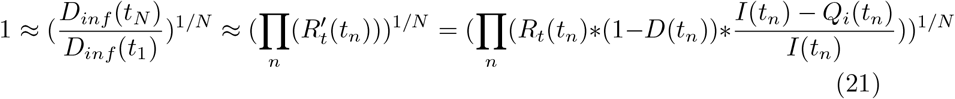
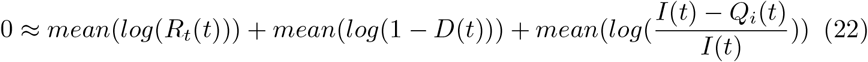
Assuming control measures don’t change drastically over time, we replace the mean of the log with the log of the mean:

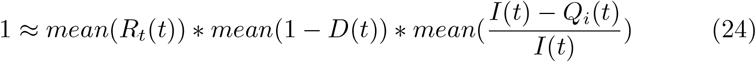
This is equivalent to Equation 1 with 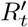 set to 1, showing that by averaging over time, the requirements for precise knowledge and control of system state can be relaxed.
set to 1, showing that by averaging over time, the requirements for precise knowledge and control of system state can be relaxed.