Exhaled CO₂ as COVID-19 infection risk proxy for different indoor environments and activities

Coronavirus disease 2019 (COVID-19) is currently sweeping the world and causing major losses of human lives (1). Lockdowns imposed to various extent worldwide for the COVID-19 transmission reduction are not supposed to be long-term measures, otherwise they would lead to unaffordable social and economic costs. On the other hand, resumption of social, educational, and business activities raises concerns about transmission resurgence.

In last few months, there has been rapidly mounting evidence for COVID-19 transmissions via aerosols (2, 3), i.e., severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-containing particles with diameters of e.g., several µm that can float in the air for minutes to hours. Transmission is much easier indoors than outdoors, which is most consistent with aerosols (3–5). As humans spend most time in indoor environments, where air volumes are limited and virus-laden aerosols may easily accumulate, mitigation of indoor COVID-19 transmissions is a subject of high interest (6, 7) and is key to a successful societal and economic reopening. Practical, affordable, and widely applicable measures to monitor and limit indoor transmission risks are urgently needed.

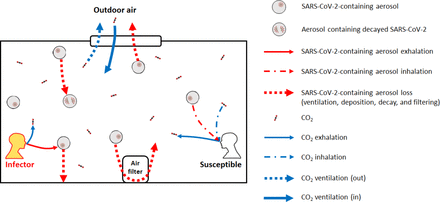
Indoor CO₂ has been suggested as a practical proxy of respiratory infectious disease transmission risk (8), as pathogen-containing aerosols and CO₂ are co-exhaled by those infected (Fig. 1). Since background (ambient) CO₂ level is stable and indoor excess CO₂ is usually only from human exhalation, measurements of indoor CO₂ concentration by low-cost CO₂ sensors can often be good indicators of infection risk and suitable for mass deployment (9, 10). However, the CO₂ level corresponding to a given COVID-19 infection risk is largely unknown. A few guideline limit concentrations have been proposed, but without solid and quantitative basis (11,12). In particular, only a single CO₂ threshold was recommended in each of these proposed guidelines. Whether a single CO₂ concentration ensures low COVID-19 infection risk in all common indoor environments remains an open question, but is also critical for effective CO₂-based mass risk monitoring.

• Download figure
• Open in new tab

Fig. 1

Schematic illustrating the exhalation, inhalation, and other loss processes of SARS-CoV-2-containing aerosols and the exhalation, inhalation, and other source and sink of CO₂ in an indoor environment.

In this study, we derive the analytical expressions of the probability of indoor COVID-19 infection through room-level aerosol transmission only (i.e., assuming social distance is kept so that close proximity aerosol and droplet pathways are eliminated; fomite transmission is not included), human-exhaled CO₂ concentration, and subsequently a few CO₂-based quantities as infection risk proxies. Based on available data, we apply these expressions to common indoor settings to answer the abovementioned open question.

To derive the SARS-CoV-2 aerosol concentration in indoor air, we assume well-mixed air (Fig. 1). SARS-CoV-2 is emitted by infectious person(s) only. Ventilation with outdoor air, virus decay and deposition onto surfaces, and additional control measures (e.g., air filtration and use of germicidal UV) result in losses of infective virus from indoor air. Other sources (e.g., virus-containing aerosol resuspension) and sinks (e.g., inhalation by humans and animals indoors) are assumed to be unable to significantly affect the SARS-CoV-2 concentration. The amount of the virus infectious doses (“quanta”) inhaled by a susceptible person (n) determines their probability of infection (P). According to the Wells-Riley model of aerosol infection (13),

One SARS-CoV-2 quantum corresponds to a probability of infection of 1-1/e (63%). The expected value of n (〈n〉) for an originally uninfected person corresponding to a given level of immunity in local population (probability of an occupant being immune, Pim), can be calculated as follows 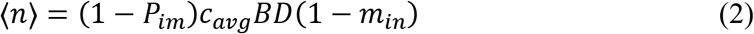where cavg, B, D, and min are the average virus concentration (quanta m^-3), breathing rate of the susceptible person (m³ h^-1), duration of the event (h), and mask filtration efficiency for inhalation, respectively. (1 − P_im) is included since quanta inhaled by an immune uninfected individual will not lead to infection and should be excluded. Under the assumption of no occupants and no SARS-CoV-2 in the indoor air at the start of the event, the analytical expression of the expected value of cavg based on the prevalence of infectors in local population (probability of an occupant being infector, PI), <cavg>, is (see Materials and Methods for the derivation) 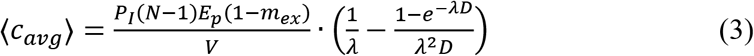where N is number of occupants, E_p is the SARS-CoV-2 exhalation rate by an infector (quanta h^-1), mex mask filtration efficiency for exhalation, V indoor environment volume (m³), and λ first-order virus loss rate coefficient (h^-1) that includes the ventilation with outdoor air and all other virus removal and deactivation processes.

If there are no other significant CO₂ sources/sinks (e.g., gas/coal stove and pets/plants), i.e., if indoor excess CO₂ (relative to the background outdoor level) production is only due to human exhalation and its loss is ventilation, similar quantities for CO₂ can be expressed as follows (see Materials and Methods for the derivation) 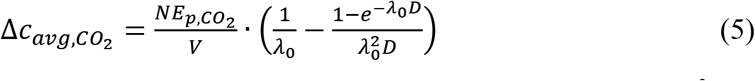where n_ΔCO2,ΔC_avg,CO2, and E_p,co2 are inhaled excess (human-exhaled) CO₂ volume (m³), excess CO₂ volume mixing ratio, and CO₂ exhalation rate per person (m³ h^-1), respectively, and λ₀ is the ventilation rate (h^-1).

When P is low, as it should be for a safe reopening, P ≈ n. As airborne SARS-CoV-2 and excess CO₂ are co-exhaled and co-inhaled, in principle n_ΔCO2 can be a proxy of ‹n›, and thus P. The ratio n_ΔCO2 of to ‹n› (in m³ quantum^-1), indicates the volume of inhaled excess CO₂ corresponding to a unit inhaled quantum. However, this quantity, involving inhaled CO₂ volume that is difficult to measure, is not practical for widespread transmission risk monitoring, which usually requires a fast decision-making process simply based on indoor CO₂ concentration reading (usually in ppm) of a low-cost sensor. Therefore, we propose, as another proxy of the risk of an environment, with PI = 0.1%, the volume mixing ratio of the excess CO₂ that an uninfected individual inhales for 1 h in that environment for .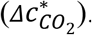

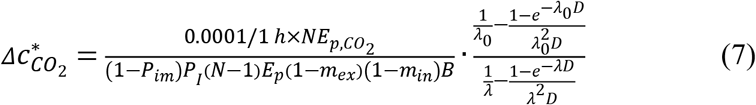
This quantity is closely related to the excess CO₂ level corresponding to the unity basic reproduction number (R0) (8) (see Materials and Methods for details), and can be directly and easily compared to CO₂ sensor readings. The ratio of the sensor reading to 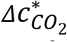is that of the probability of infection of an originally uninfected person in that environment for 1 h to 0.01%. P = 0.01% being chosen as reference does not imply safety at this P in all situations, since when N and/or D are large, and/or the event is repeated many times (e.g., in school/university settings), the overall probability of infection for one susceptible person and/or total infections may still be significant.

is a function of a number of variables. A priori, varying any of them can result in a different value of even for similar settings. As an example, we study a set of model cases for a typical university class. The cases are specified in Table S1. The 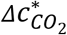and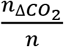 in these cases are shown in Fig. 2A and S1A, respectively.

• Download figure
• Open in new tab

Fig. 2.

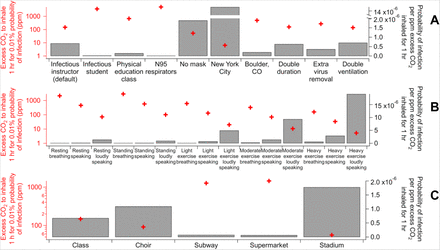
Excess CO₂ volume mixing ratio (ppm) that an uninfected individual inhales for 1 h for a probability of infection of 0.01% 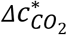and probability of infection per ppm excess CO₂ inhaled for 1 hr (inversely proportional to 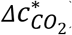) for (A) variants of the university class case (see Table S1 for the case details), (B) various activities (see Table S2 for details of the activities), and (C) several indoor environments(see Table S3 for the case details).

In the base class case, the infector is assumed to be the instructor. Compared to the case with a student being infector, 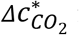in the base case is ∼1.5 orders of magnitude lower, just because the vocalization of the instructor, who usually speaks, greatly enhances E_p (14, 15), while virus exhalation by students, who are assumed here to speak little, is much less efficient. In the case of a physical education (PE) class in the same indoor environment, where occupants are assumed to be doing heavy exercise and no talking, 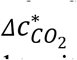is much lower than for the infected student case in a traditional lecture (Fig. 2A). Compared to sitting, heavy exercise increases both occupants’ virus and CO₂ exhalation rates to similar extents (14–16), which does not significantly change 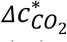. However, breathing rates of occupants doing intense activities are much higher than those sitting (17). Even if CO₂ and SARS-CoV-2 concentrations are the same as in the infected student case, a susceptible person in the PE class case can still inhale a larger dose of SARS-CoV-2 and more excess CO₂, and have a remarkably different P. As a result, a single recommendation of indoor CO₂ threshold is not valid even for a series of school settings.

According to Eqs. 2 and 3, whether occupants wear masks and what masks they wear can make a substantial difference in infection risk through virus filtration in the same indoor setting. However, masks do not filter CO₂. The base class case (with surgical masks), that with all occupants wearing N95 respirators, and that with no mask use have identical CO₂ mixing ratios, but up to ∼2 orders of magnitude different P (Table S1) due to filtration of virus-containing particles by mask. Therefore, for the same P of 0.01%, the base class case has a corresponding excess CO₂ level x∼30 lower than the case with all occupants wearing N95 respirators, but x∼2 higher than the case with no mask use (Fig. 2A).

PI is obviously another important factor governing the infection risk, as P proportional to it. Again, it has no impact on CO₂. Compared to the base class case (PI = 0.001), the estimated situation of New York City in April (PI = 0.023) and of Boulder, CO in June (PI = 0.0003) have x∼20 higher and x∼2 lower P, respectively, (Table S1), and hence Δc_co2(1 h,p = 0.01%) lower and higher to the respective extents (Fig. 2A). However, Pim usually cannot result in a difference in P greater than a factor of 2 under conditions of interest, since if Pim > 50%, the population has reached or is close to herd immunity (18) and widespread transmission risk monitoring is no longer needed.

According to Eq. 7, the other variables that can affect 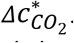are N, D, λ, and λ0. 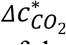is generally not highly sensitive to them, although some of them (e.g., λ) can have a large impact on P. As long as occupants are not only a few, , where N plays a role in Eq. 7, is close to 1.

The fraction term involving D, λ, and λ0 (after the product sign) in Eq. 7 usually does not deviate from 1 substantially (Fig. S2). It is close to 1 when λD is very small, and λ/λ0 when λD is very large. As long as the indoor environment is not very poorly ventilated nor equipped with very strong virus removal setups (e.g., substantial filtering of recirculated air, portable HEPA filters, germicidal UV), λ/λ0 is relatively close to 1. Compared to the base classroom case (λ/λ0 ∼ 1.3), doubling the duration or ventilation brings minimal changes to 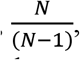. Increasing λ/λ0 to ∼3 by additional virus control measures increases more significantly, as those measures do not remove CO₂. But this change is still within a factor of 2 for the range of control measures in these examples (Fig. 2A).

As discussed above, occupants’ activities indoors, to which Ep, E_p,co2, and B are all related, are a major or dominant factor governing the infection risk. We thus compile the data of these parameters as a function of activity (intensity and vocalization degree) (Table S2). Note that this compilation has large uncertainties from Ep data (14, 15) and matching of activity categories, which are all classified differently for Ep, E_p,co2, and B (see Materials and Methods for details). Moreover, these uncertainties are currently impossible to quantify. However, the trends shown by the data are clear and thus able to reveal the relative risk of these activities with confidence. Simply, the stronger vocalization, the higher risk, and the more intense activity, the higher risk. We calculate for these activities when N is large, D = 1 h, PI = 0.001, λ0 = 3 h⁻¹, λ = 4 h⁻¹, no mask is used (Fig. 2B), a setting similar to the class case. Three class cases, i.e., base, infected student, and PE cases, can be easily related to the activity categories of “Standing – loudly speaking”, “Resting – breathing”, and “Heavy exercise – breathing”, respectively. The related pairs have 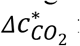within x∼2 and their mask use setting and close but different Ep, E_p,co2, and B values can largely explain the differences in.

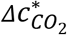Then we apply this analysis to a range of real-world settings, in addition to the class case, i.e., the Skagit County choir superspreading event (19), a subway car, a supermarket (focused on a worker), and an event in a stadium, which, though outdoors, often has somewhat stagnant air allowing virus-laden aerosols to build up and thus can be treated similarly as an indoor environment (see Table S3 for the specifications of these cases). Figures 2C and S1B shows their 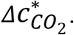and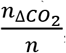, respectively. Again, these values span orders of magnitude. We can still relate these cases to the activity categories of “Standing – loudly speaking”, “Resting – breathing”, “Light exercise – breathing” (or “Light exercise – speaking”), and “Light exercise – speaking” (or “Light exercise – loudly speaking”), respectively.

For the actual choir case, its PI is an order of magnitude lower than 0.1% while the estimated Ep is an order of magnitude higher (19), resulting in a similar 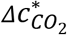to that of “Standing – loudly speaking” shown in Fig. 2B. 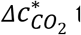in the stadium case is between those of “Light exercise – speaking” and “Light exercise – loudly speaking”, as both activities may happen in the event. The difference of 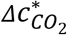between the supermarket case and its related activities shown in Fig. 2B is mainly due to the long duration of the event (8 h). 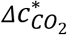of the supermarket case divided by D leads to the excess CO₂ threshold for the worker to inhale over 8 h between those of “Light exercise – breathing” and “Light exercise – speaking”. of the subway case is ∼1/3 lower than that of “Resting – breathing” in Fig. 2B because of the short duration (0.33 h) and mask use (universal use of surgical masks or equivalent).

As shown above, the infection risk analysis for various settings can be based on the relevant activities with adjustments for PI, D, mask use etc. For policy-making concerning acceptable indoor CO₂ level, we also recommend an activity-dependent approach. Reference excess CO₂ levels for indoor environments with certain types of activities mainly involved can be found in Fig. 2B. Then this mixing ratio can be scaled for typical D (by multiplying it) and target P (by multiplying its ratio to 0.01%) to obtain an excess CO₂ threshold, which may be relaxed a little further depending on the local mask policy. The sum of this value and the outdoor CO₂ concentration, i.e., ∼410 ppm (20), is the final recommended indoor CO₂ concentration threshold. This procedure is relatively easy to implement at local and even individual business levels but has a much stronger scientific basis than one-threshold-for-all approaches. Calculations for other scenarios can be easily performed with the online COVID-19 aerosol transmission estimator (21).