Abstract
The COVID-19 pandemic has created an urgent need for models that can project epidemic trends, explore intervention scenarios, and estimate resource needs. Here we describe the methodology of Covasim (COVID-19 Agent-based Simulator), an open-source model developed to help address these questions. Covasim includes demographic information on age structure and population size; realistic transmission networks in different social layers, including households, schools, workplaces, and communities; age-specific disease outcomes; and intrahost viral dynamics, including viral-load-based transmissibility. Covasim also supports an extensive set of interventions, including non-pharmaceutical interventions, such as physical distancing, hygiene measures, and protective equipment; and testing interventions, such as symptomatic and asymptomatic testing, isolation, contact tracing, and quarantine. These interventions can incorporate the effects of delays, loss-to-follow-up, micro-targeting, and other factors. In collaboration with local health agencies and policymakers, Covasim has already been applied to examine disease dynamics and policy options in Africa, Europe, Oceania, and North America.
1 Introduction
Governments are faced with an urgent need to understand the rapidly evolving COVID-19 pandemic landscape and translate it into policy. Since the onset of the pandemic, mathematical modeling has been at the heart of informing this decision-making. Numerous COVID-19 models and data visualization and interpretation tools have been developed over the last several months in an attempt to meet this demand, with varying purposes, structures, and levels of detail and complexity. Data dashboards and statistical models, such as the model from the Institute for Health Metrics and Evaluation (IHME COVID-19 Team & Murray, 2020), are useful for understanding the current state of the epidemic. However, more detailed models are needed to evaluate scenarios based on complex intervention strategies. These strategies are increasingly important to evaluate, as we aim to balance epidemiological and economic factors in reopening economies.
Models for examining COVID-19 transmission and control measures can be broadly divided into two main types: compartmental models and agent-based (or microsimulation) models, with the former generally being simpler and faster, while the latter are generally more complex, detailed, and computationally expensive. Numerous compartmental models have been developed or repurposed: Walker et al. (2020) used an age-structured stochastic SEIR model to determine the global impact of COVID-19 and the effect of various social distancing interventions to control transmission and reduce health system burden; Read et al. (2020) developed an SEIR model to estimate the basic reproductive number in Wuhan; and Keeling et al. (2020) use one to look at the efficacy of contact tracing as a containment measure. In models such as those by Giordano et al. (2020) and Zhao and Chen (2020), compartments are further divided to provide more nuance in simulating progression through different disease states, and have been deployed to study the effects of various population-wide interventions such as social distancing and testing on COVID-19 transmission.
For microsimulation models, several agent-based influenza pandemic models have been repurposed to simulate the spread of COVID-19 transmission and the impact of social distancing measures in Australia (Chang et al., 2020), Singapore (Koo et al., 2020), the United States (Chao et al., 2020), and the United Kingdom (Ferguson et al., 2020). Additionally, agent-based models have been developed to evaluate the impact of social distancing and contact tracing (Aleta et al., 2020; Kretzschmar et al., 2020; Kucharski et al., 2020). Features of these models include accounting for the number of household and non-household contacts (Chao et al., 2020; Kretzschmar et al., 2020; Kucharski et al., 2020); the age and clustering of contacts within households (Aleta et al., 2020; Chao et al., 2020; Kucharski et al., 2020); and the microstructure in schools and workplace settings informed by census and time-use data (Aleta et al., 2020). Branching process models have also been used to investigate the impact of non-pharmaceutical intervention strategies (Hellewell et al., 2020; Peak et al., 2017).
In developing Covasim, our aim was to capture the benefits of agent-based modeling (in particular, the ability of such models to simulate the kinds of microscale policies being used to respond to the COVID-19 pandemic), whilst also using the best-available computational methods in order to minimize the complexity and computational time usually associated with such models.
The primary aim of this paper is to describe the Covasim methodology. Section 2 describes Covasim’s disease progression model, transmission dynamics, population and network structure, available interventions, as well as additional features, performance characteristics, and implementation details. Section 3 presents several brief examples illustrating some of the different analyses and use cases that are supported by Covasim, while Section 4 reviews the limitations of Covasim and discusses future work.
2 Methods
2.1 Overview
Covasim simulates the state of individual people, known as agents, over a number of discrete time steps. Conceptually, the model is largely focused on a single type of calculation: the probability that a given agent on a given time step will change from one state to another, such as from susceptible to infected, or from critically ill to dead. Once these probabilities have been calculated, a pseudorandom number generator with a user-specified seed is used to determine whether the transition actually takes place for a given model run.
The logical flow of a single Covasim run is as follows. First, the simulation object is created, then the parameters are loaded and validated for internal consistency, and any specified data files are loaded (described in Section 2.6.5). Second, a population is created, including age, sex, and comorbidities for each agent, drawing from location-specific data distributions where available. Third, agents are connected into contact networks based on their age and other statistical properties (Section 2.4). Next, the integration loop begins. On each timestep (which corresponds to a single day by default), the order of operations is: dynamic rescaling (Section 2.6.3); applying health system constraints (Section 2.6.1); updating the state of each agent, including disease progression (Section 2.2); importation events (Section 2.6.2); applying interventions (Section 2.5); calculating disease transmission events across each infectious agent’s contact network (Section 2.3); and the collation of outputs into results arrays (Section 2.6.6). The following sections describe each step in more detail.
2.2 Disease progression
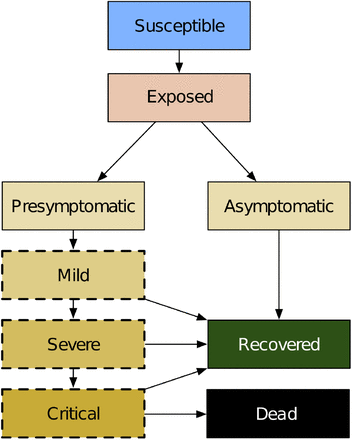
In Covasim, each individual is characterized as either susceptible, exposed (i.e., infected but not yet infectious), infectious, recovered, or dead, with infectious individuals additionally categorized according to their symptoms: asymptomatic, presymptomatic, mild, severe, or critical. A schematic diagram of the model structure is shown in Figure 1.
Covasim model structure, including infection (exposure), disease progression, and final outcomes. Yellow shading indicates that an individual is infectious and can transmit the disease to other susceptible agents. States with a dashed border are considered symptomatic with respect to symptomatic versus asymptomatic testing.
The length of time after exposure before an individual becomes infectious is assumed to follow a log-normal distribution with a mean of 4.6 days, which is within the range of values reported across the literature (Table 1). The length of time between the start of viral shedding and symptom onset is assumed to follow a log-normal distribution with a mean of 1 day (Table 1). Exposed individuals may develop symptoms or may remain asymptomatic. Individuals with symptoms are disaggregated into either mild, severe, or critical cases, with the probability of developing a more acute case increasing with age (Table 2). Covasim can also model the effect of comorbidities, which act by modifying an individual’s probability of developing severe symptoms (and hence critical symptoms and death). By default, comorbidity multipliers are set to 1 since they are already factored into the marginal age-dependent disease progression rates.
Default duration parameters, in days, used in the Covasim model.
Age-linked disease susceptibility, progression, and mortality probabilities. Key: psus: probability of developing symptoms; psym: probability of developing symptoms; psev: probability of developing severe symptoms (i.e., sufficient to justify hospitalization); pcri: probability of developing into a critical case (i.e., sufficient to require ICU); pdeath: probability of death. Susceptibility values are derived from Zhang et al. (2020); all other values are derived from Verity et al. (2020)and Ferguson et al. (2020). *Overall values depend on the age structure of the population being modeled. For a population like the US or UK, the symptomatic proportion is roughly 0.7, while for populations skewed towards younger ages, the symptomatic proportion is lower.
Estimates of the duration of COVID-19 symptoms and the length of time that viral shedding occurs are highly variable, but durations are generally reported to increase according to acuity (Bi et al., 2020; Yang et al., 2020). We reflect this in our model with different recovery times for asymptomatic individuals, those with mild symptoms, and those with severe symptoms, as summarized in Table 1. All non-critical cases are assumed to recover, while critical cases either recover or die, with the probability of death increasing with age (Table 2).
2.3 Transmission and within-host viral dynamics
Whenever a susceptible individual comes into contact with an infectious individual on a given day, transmission of the virus occurs according to probability β. For a well-mixed population where each individual has an average of 20 contacts per day, a value of β = 0.016 corresponds to a doubling time of roughly 4–6 days and an R0 of approximately 2.2-2.7, where the exact values depend on the population size, age structure, and other factors). The value of β = 0.016 is used as the default in Covasim; however, this value is typically calibrated by the user to best match local epidemic data.
If realistic network structure (i.e., households, schools, workplaces, and community contacts) is included, the value of β depends on the contact type. Default transmission probabilities are roughly 0.1 per contact per day for households, 0.02 for workplaces, 0.01 for schools, and 0.002 for the community. These values correspond to relative weightings of 50:10:5:1, with a weighted mean close to the default β value of 0.016 for a well-mixed population (i.e., if different network layers are not used). When combined with the default number of contacts in each layer, age-based susceptibility, and other factors, for a typical (unmitigated) transmission scenario, the proportions of transmission events that occur in each contact layer are approximately 40% via households, 35% via workplaces, 10% via schools, and 15% via the community. The value of β can also be modified by interventions, such as physical distancing, as described below.
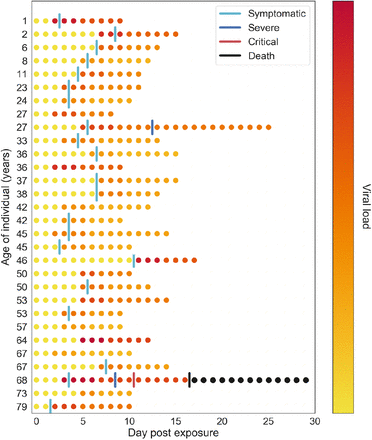
In addition to allowing individuals to vary across disease severity and time spent in each disease state, we allow individual infectiousness to vary between people and over time. We use individual viral load to model these differences in infectivity. Several groups have found that viral load is highest around the time of symptom onset, or possibly even before that, and then falls monotonically (D. He et al., 2020; Lescure et al., 2020; To et al., 2020; Zou et al., 2020). As a first approximation to this viral time course, we model two stages of viral load: an early high stage followed by a longer low stage. By default, we set the viral load of the high stage to be twice as high as the low stage and to last for 30% of the infectious duration or 4 days, whichever is shorter. The default viral load for each agent is drawn from a log-normal distribution with mean 0.84 and standard deviation 0.30 (Endo et al., 2020). The daily viral load is used to adjust the per-contact transmission probability (β) for an agent on a given day (Figure 2).
Example of within-host viral load dynamics in Covasim. Each row shows a different agent in the model. Color indicates viral load, which typically peaks the day before or the day of symptom onset, before declining slowly.
Schematic diagram of contact networks with multiple layers in Covasim.
Evidence is mixed as to whether transmissibility is lower if the infectious individual does not have symptoms (D. He et al., 2020). We take a default assumption that it is not, but include a parameter that can be modified as needed depending on the modeling application or context.
2.4 Contact network models
Covasim is capable of generating and using three alternative types of contact networks: random networks, SynthPops networks, and hybrid networks. Each of these may be useful in different settings, and in addition users have the option of defining their own networks. A comparison of the main features and use cases of each of Covasim’s default network model options is shown in Table 3, and details on each are provided in the following sections. In addition, to facilitate easy adaptation to different contexts, Covasim comes pre-loaded with data on country age distributions and household sizes as reported by the UN Population Division, 2019.
Comparison of population options in Covasim.
2.4.1 Random networks
Covasim generates random networks by assuming that each person in the modeled population can come into contact with anyone else in the population. Each person is assigned a number of daily contacts, which is drawn from a Poisson distribution whose mean value can be specified by the user depending on the modeling context (with a default value of 20). The user can also decide whether these contacts should remain the same throughout the simulation, or whether they should be sampled randomly from the population each day.
2.4.2 SynthPops networks
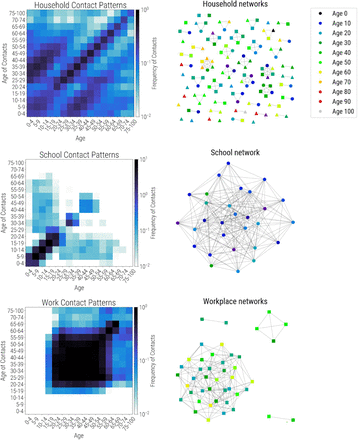
Covasim is integrated with SynthPops, an open-source data-driven model capable of generating realistic synthetic contact networks for populations; further information, including documentation and source code, is available from synthpops.org. Briefly, the method draws upon previously published models and empirical studies to infer high-resolution age-specific contact patterns in key settings (e.g., households, schools, workplaces, and the general community) relevant to the transmission of infectious diseases (Fumanelli et al., 2012; Mistry et al., 2020; Smieszek et al., 2014). Census and municipal data are used by SynthPops to inform demographic characteristics (e.g., age, household size, school enrollment, employment rates). Age-specific contact matrices (such as those in Prem et al., 2017) are then used to generate individuals and their expected contacts in a multilayer network framework. By default, SynthPops generates household, school, and work contact networks; community connections are generated using the random approach described above. An example synthetic network as generated by SynthPops is shown in Figure 4.
Synthetic population networks for households (top), schools (middle), and workplaces (bottom). Age-specific contact matrices are shown on the left, while actual connectivity patterns for a 127-person subsample of a population of 10,000 individuals are shown on the right. All individuals are present in the household network, including some with no household connections. A subset of these individuals, including teachers, are present in the school network (circles); another subset is present in workplace networks (squares); some individuals are in neither school nor work networks (triangles).
2.4.2.1 Households
SynthPops uses data on the distribution of ages, household sizes, and the age of reference individuals conditional on household size for a given population, to generate individuals within households. The algorithm first generates household sizes from the household size distribution, and then assigns a reference individual (for example, the head of the household) with their sampled age conditional on the household size. To construct the other household members, age mixing contact matrices are used to infer the likely ages according to the age of the reference person and the population age distribution adjusted for non-reference ages.
2.4.2.2 Schools
A similar approach is used to construct schools. Census and municipal school data, or survey data such as from Demographic and Health Surveys (Huisman & Smits, 2009), can be used to inform enrollment rates by age, school sizes, and student-teacher ratios. The SynthPops algorithm first chooses a reference student for the school conditional on enrollment rates to infer the school type, and then uses the age mixing contact matrix in the school setting to infer the likely ages of the other students in the school. Students are drawn from an ordered list of households, such that they reproduce an approximation of the neighborhood dynamics of children attending area schools together. Teachers are drawn from the adult population comprising the labor force and assigned to schools as needed, reflecting average student-teacher ratio data.
2.4.2.3 Workplaces
The labor force is drawn using employment rates by age, and non-teachers are assigned to workplaces using data on establishment sizes. Workers are assigned to workplaces using a similar method with an initial reference worker sampled from the labor force and their co-workers inferred from age mixing patterns within the workforce. All workers (teachers included) are drawn at random from the population, to reflect the general mixing of adults from different neighbourhoods at work.
For contacts in the general community, we draw n random contacts for each individual on a daily basis from other individuals in the population, where n is drawn from a Poisson distribution with rate parameter λ equal to the expected number of contacts in the general community (with λ = 20 as a default, as above). Connections in this layer reflect the nature of contacts in shared public spaces like parks and recreational spaces, shopping centres, community centres, and public transportation. All links between individuals are considered undirected to reflect the ability of either individual in the pair to infect each other.
The generated multilayer network of household, school, work, and general community network layers presents a population with realistic microstructure. This framework can also be extended to consider more detailed interactions in key additional settings, such as hospitals, encampments, shelters for those experiencing homelessness, and assisted living facilities.
2.4.3 Hybrid networks
Covasim contains a third option for generating contact networks, which captures some of the realism of the SynthPops approach but does not require as much input data, and is more readily adaptable to other settings. As such, it is a “hybrid” approach between a fully random network and a fully data-derived network. As with SynthPops, each person in the population has contacts in their household, school (for children), workplace (for adults), and community. A population of individuals is generated according to a location-specific age distribution, and each individual is randomly assigned to a household using location-specific data on household sizes.
Unlike SynthPops, the hybrid algorithm does not account for the distribution of ages within a household. Children are assigned to schools and adults to workplaces, each with a user-specified number of fixed daily contacts (by default, Poisson-distributed with means of 20 for schools and 8 for workplaces). Individuals additionally have contacts with others in the community (by default, Poisson distributed with a mean of 20). All children and young adults aged between 6 and 22 are assigned to schools and universities, and all adults between 22 and 65 are assigned to workplaces. This distinguishes it from SynthPops where enrollment or employment varies depending on the given data. A comparison of the different population structure options available in Covasim is listed in Table 3.
2.5 Interventions
A core function of Covasim is modeling the effect of interventions on disease transmission or health outcomes, to understand the impact that different policy options may have in a specific setting. In general, interventions are modeled as changes to parameter values. Covasim has built-in implementations of the common interventions described below, as well as the ability for users to create their own interventions.
2.5.1 Physical distancing and hygiene
The most basic intervention in Covasim is to reduce β (transmissibility) starting on a given day. This can be used to reflect both (a) reductions in transmissibility per contact, such as through mask wearing, personal protective equipment, hand-washing, and maintaining physical distance; and (b) reductions in the number of contacts at home, school, work, or in the community. However, Covasim also includes an “edge-clipping” intervention (considering a contact between two agents as a weighted “edge” between two “nodes”), where β remains unchanged but the number of contacts that person has is reduced. Complete school and workplace closures, for example, can be modeled either by setting β to 0, or by removing all edges in those contact layers; partial closures can be modeled by smaller reductions in either β or the number of contacts.
In general, both types of interventions have similar impact – for example, halving the number of contacts and keeping β constant will produce very similar epidemic trajectories as halving β and keeping the number of contacts constant. However, the distinction becomes important when considering the interaction between physical distancing and other interventions. For example, in a contact tracing scenario, the number of contacts who require tracing, number of tests performed, and number of people placed in quarantine are all strongly affected by whether physical distancing is implemented as a reduction in β of a specific edge, or removing that edge entirely.
2.5.2 Testing and diagnosis
Testing can be modelled in two different ways within Covasim, depending on the format of testing data and purpose of the analysis. The first method allows the user to specify the probabilities that people with different risk factors and levels of symptoms will receive a test on each day. Separate daily testing probabilities can be entered for those with/without symptoms, and those in/out of quarantine. The model will then estimate the number of tests performed on each day. The second method allows the user to enter the number of tests performed on each day directly, including multipliers on the probability of a person receiving a test if they have symptoms, are in quarantine, or are over a certain age. This method will then allocate the tests among the population.
Once a person is tested, the model contains a delay parameter that indicates how long people need to wait for their results, as well as a loss-to-follow-up parameter that indicates the probability that people will not receive their results. Additional parameters control the sensitivity and specificity of the tests.
2.5.3 Contact tracing
Contact tracing corresponds to notifying individuals that they have had contact with a confirmed case, so that they can be quarantined, tested, or otherwise change their behavior. Contact tracing in Covasim is parameterized by the probability that a contact can be traced, and by the time taken to identify and notify contacts. Both parameters can vary by type of contact, and can be controlled by the user. For example, it may be reasonable to assume that people can trace members of their household immediately and with 100% probability, while tracing work colleagues may take several days and may be incomplete.
2.5.4 Isolation of positives and contact quarantine
Isolation (referring to behavior changes after a person is diagnosed with COVID-19) and quarantine (referring to behavior changes after a person is identified as a known contact of someone with confirmed or suspected COVID-19) are the primary means by which testing interventions reduce transmission. In Covasim, people diagnosed with COVID-19 can be isolated. Their contacts who have been traced can be placed in quarantine with a specified level of compliance; people in quarantine may also have an increased probability of being tested. People in isolation or quarantine typically have a lower probability of infecting others (if infectious) or of acquiring COVID-19 (if quarantined and susceptible), with the default reduction being 80%. The efficacy of isolation or quarantine varies by environment; isolation or quarantine at home may mean that there is actually a higher probability of passing on infection to, or acquiring infection from, other household members, while the probabilities of transmission or acquisition from school, work, or community contacts may be reduced.
2.5.5 Pharmaceutical and user-defined interventions
Pharmaceutical interventions, including antiviral treatments and vaccines, are not explicitly implemented in Covasim due to the large considerable uncertainties regarding their eventual characteristics and availability. However, they can be defined by adapting existing Covasim interventions. For example, each agent in the model has a relative susceptibility parameter, which is a multiplicative factor on their risk of infection per exposure event. A vaccine of a given efficacy (which could include waning efficacy or increased efficacy from multiple doses) could be implemented by reducing an agent’s relative susceptibility after receiving the vaccine. Similarly, antiviral treatments could be modeled by modifying an individual’s probabilities of progression to severe disease, critical disease, and death, and by modifying their relative transmissibility.
Each intervention has full access to the simulation object at each timestep, which means that user-defined interventions can dynamically modulate any aspect of the simulation. This can be used to create interventions more specific than those included by default in Covasim; for example, age-specific physical distancing or quarantine. However, interventions can also be used for other purposes: for example, it is possible to define an “intervention” that, at each timestep, records additional details about the internal state of the model that are not included as standard outputs.
2.6 Additional features
2.6.1 Health system capacity
Individuals in the model who have severe and critical symptoms are assumed to require regular and ICU hospital beds, respectively, including ventilation in the latter case. The number of available ICU beds is an input parameter; if the current number of critical cases is greater than the number of available beds, then the health system capacity is exceeded, and critically ill individuals who are unable to access treatment have an increased mortality rate (by default, by a factor of 2, corresponding to virtually all critical cases dying).
2.6.2 Importations
The spatial movement of agents is not explicitly modeled in Covasim, and the population size for a given simulation is fixed. Thus, importations are implemented as spontaneous infections among the susceptible population. This corresponds to agents who become infected elsewhere and then return to the population.
2.6.3 Dynamic scaling
One of the major challenges with agent-based models is simulating a sufficient number of agents to capture an epidemic at early, middle, and late stages, without requiring cumbersome levels of memory or processor usage. Whereas compartmental SEIR models require the same amount of computation time regardless of the population size being modeled, the performance of agent-based models typically scales linearly or supralinearly with population size (see Section 2.7.1). As a consequence, many agent-based models, including Covasim, include an optional “scaling factor”, where a single agent in the model is assumed to represent multiple people in the real world. A scaling factor of 10, for example, corresponds to the assumption that the epidemic dynamics in a city of 2 million people can be considered as the sum of the epidemic dynamics of 10 identical subregions of 200,000 people each.
However, the limitation of this approach is that it introduces a discretization of results: model outputs can only be produced in increments of the scaling factor, so relatively rare events, such as deaths, may not have sufficient granularity to reflect the epidemic behavior at a small scale. In addition, using too few agents in the model introduces stochastic variability patterns that do not reflect real-world processes in the entire population.
To circumvent this, Covasim includes an option for dynamic scaling. Initially, when the epidemic is small, there is no scaling performed: one agent corresponds to one person. Once a certain threshold is reached, however (by default, 5% of the population), the non-susceptible agents in the model are downsampled and a corresponding scaling factor is introduced (by default, a factor of 2 is used). For example, in a simulation of 100,000 agents representing a true population of 1 million, dynamic scaling would be triggered when cumulative infections surpass 5,000, leaving 95,000 susceptible agents; dynamic rescaling would resample the non-susceptible population to 2,500 (representing 5,000 people) and increase the number of susceptible agents to 97,500 (representing 195,000 people), with every agent now counting as two. If the epidemic expands further, this process will repeat iteratively until the scale factor reaches its upper limit (which in this example is 10, and which would be reached after 50,000 cumulative infections). Through this process, arbitrarily large populations can be modeled, even starting from a single infection, maintaining a constant level of precision and computation time throughout.
2.6.4 Model outputs
By default, Covasim outputs three main types of result: “stocks” (e.g., the number of people with currently active infections on a given day), “flows” (e.g., the number of new infections on a given day), and “cumulative flows” (e.g., the cumulative number of infections up to a given day). For states that cannot be transitioned out of (e.g. death or recovery), the stock is equal to the cumulative flow. Flows that are calculated in the model include: the number of new infections and the number of people who become infectious on that timestep; the number of tests performed, new positive diagnoses, and number of people placed in quarantine; the number of people who develop mild, severe, and critical symptoms; and the number of people who recover or die. The date of each transition (e.g., from critically ill to dead) is also recorded. By default, these results are summed over the entire population on each day; results for subpopulations can be obtained by defining custom “interventions”, as described in Section 2.5.5.
In addition to these core outputs, Covasim includes several outputs for additional analysis. For example, several methods are implemented to compute both doubling time and the effective reproductive number Reff. By default, the epidemic doubling time is computed using the “rule of 70” (Bakir, 2016), specifically:
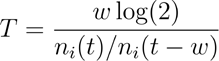 where T is the doubling time, w is the window length over which to compute the doubling time (3 days by default), and ni(t) is the cumulative number of infections at time t.
where T is the doubling time, w is the window length over which to compute the doubling time (3 days by default), and ni(t) is the cumulative number of infections at time t.
Numerous definitions of the effective reproductive number exist. In standard SIR modeling, the most common definition (“method 1”) is (Barratt & Kirwan, 2010):
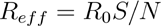 where R0 is the basic reproductive number, S is the number of susceptibles, and N is the total population size. However, with respect to COVID-19, many authors instead define Reff to include the effects of interventions, due to the implications that Reff = 1 has for epidemic control. A second common definition of Reff (“method 2”) is to first determine the total number of people who became infectious on day t, then count the total number of people these people went on to infect, and then divide the latter by the former. “Method 3” is the same as method 2, except it counts the number of people who stopped being infectious on day t (i.e., recovered or died), and then count the number of people those people infected. While methods 2 and 3 are implemented in Covasim, they have the disadvantage that they introduce significant temporal blurring, due to the potentially long infectious period (and, for method 3, the long recovery period). To avoid this limitation, the default method Covasim uses for computing Reff is to divide the number of new infections on day t by the number of actively infectious people on day t, multiplied by the average duration of infectiousness.
where R0 is the basic reproductive number, S is the number of susceptibles, and N is the total population size. However, with respect to COVID-19, many authors instead define Reff to include the effects of interventions, due to the implications that Reff = 1 has for epidemic control. A second common definition of Reff (“method 2”) is to first determine the total number of people who became infectious on day t, then count the total number of people these people went on to infect, and then divide the latter by the former. “Method 3” is the same as method 2, except it counts the number of people who stopped being infectious on day t (i.e., recovered or died), and then count the number of people those people infected. While methods 2 and 3 are implemented in Covasim, they have the disadvantage that they introduce significant temporal blurring, due to the potentially long infectious period (and, for method 3, the long recovery period). To avoid this limitation, the default method Covasim uses for computing Reff is to divide the number of new infections on day t by the number of actively infectious people on day t, multiplied by the average duration of infectiousness.
2.6.5 Data inputs
In addition to the demographic and contact network data available via SynthPops, Covasim includes interfaces to automatically load COVID-19 epidemiology data, such as time series data on deaths and diagnosed cases, from several publicly available databases. These databases include the Corona Data Scraper (coronadatascraper.com), the European Centre for Disease Prevention and Control (ecdc.europa.eu), and the COVID Tracking Project (covidtracking.com). At the time of writing, these data are available for over 4,000 unique locations, including most countries in the world (administrative level 0), all US states and many administrative level 1 (i.e., subnational) regions in Europe, and some administrative level 2 regions in Europe and the US (i.e., US counties).
2.6.6 Calibration
The process of calibration involves finding parameter values that minimize the difference between observed data (which typically includes daily confirmed cases, hospitalizations, deaths, and number of tests conducted) and the model predictions. In practice, minimizing the difference between the model and data equates to maximizing a log-likelihood function. Since most data being calibrated to are time series count data, this function is defined as:
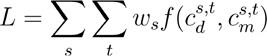 where s is a time series of observations (such cumulative confirmed cases or number of deaths); t is the time index; ws is the weight associated with s;
where s is a time series of observations (such cumulative confirmed cases or number of deaths); t is the time index; ws is the weight associated with s; 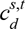 and
and 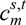 are the counts from the data and model, respectively, for this time series at this time index; and f is the Poisson test statistic as defined in Mathews (2010). By default, if data are loaded into a simulation, Covasim calculates the log-likelihood using this method.
are the counts from the data and model, respectively, for this time series at this time index; and f is the Poisson test statistic as defined in Mathews (2010). By default, if data are loaded into a simulation, Covasim calculates the log-likelihood using this method.
Calibrating any model to the COVID-19 epidemic is an inherently difficult task: not only is there significant uncertainty around the reported data, but there are also many possible combinations of parameter values that could give rise to these data. Thus, in a typical calibration workflow, most parameters are fixed at the best available values from the literature, and only essential parameters (for example, β) are allowed to vary.
Currently, calibration must be performed externally to Covasim. However, since a single model run returns a scalar log-likelihood value, these runs can be easily integrated into standardized calibration frameworks. An example implementation using Weights & Biases (wandb.com) is included in the codebase, but any standard optimization library – such as the optimization module of SciPy – can be easily adapted, as can more advanced methods such as the adaptive stochastic descend method of the Sciris library (Kerr et al., 2018), or Bayesian approaches such as history matching (Andrianakis et al., 2015).
2.7 Software architecture
Covasim was developed for Python 3.7 using the SciPy (scipy.org) ecosystem (Virtanen et al., 2020). It uses NumPy (numpy.org), Pandas (pandas.pydata.org), and Numba (numba.pydata.org) for fast numerical computing; Matplotlib (matplotlib.org) and Plotly (plotly.com) for plotting; and Sciris (sciris.org) for data structures, parallelization, and other utilities.
The source code for Covasim is available via both the Python Package Index (via pip install covasim) and GitHub (github.com/institutefordiseasemodeling/covasim). Covasim is fully open-source, released under the Creative Commons Attribution-ShareAlike 4.0 International Public License. More information is available at covasim.org, with full documentation at docs.covasim.org.
2.7.1 Performance
All core numerical algorithms in the Covasim integration loop - specifically, calculating intra-host viral load, per-person susceptibility and transmissibility, and which contacts of an infected person become infected themselves - are implemented as highly optimized 32-bit array operations in Numba. For further efficiency, agents are not represented as individual objects, but rather as indices of one-dimensional state arrays (Figure 5). This approach avoids the need to use an explicit for-loop over each agent on every integration timestep. Similarly, contacts between all agents in the model are stored as a single array of “edges” per contact layer.
Illustration of the standard object-oriented approach for implementing agent-based models (top), where each agent is a separate object, compared with the approach used in Covasim (bottom), where agents are represented as slices through a set of state arrays. Dots (…) represent omitted entries; in practice, each agent has 39 states, and there are typically tens or hundreds of thousands of agents.
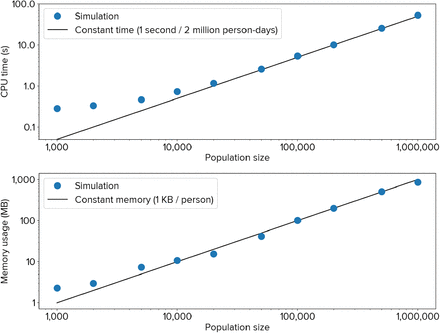
As shown in Figure 6, these software optimizations allow Covasim to achieve performance comparable to C++, despite being implemented purely in Python. Performance scales linearly with population size over multiple orders of magnitude: memory scales at a rate of roughly 1 KB per agent, while compute time (benchmarked on an Intel i9-8950HK laptop processor) scales at a rate of roughly 2 million simulated person-days per second of CPU time. Thus, it is feasible to run realistic scenarios, such as tens of thousands of infections among a susceptible population of hundreds of thousands of people for a duration of several months, in under a minute on a personal laptop.
Covasim performance in terms of processor usage (top) and memory usage (bottom), showing linear scaling over almost three orders of magnitude of population size.
2.7.1 Deployment
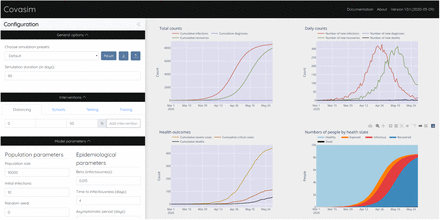
For ease of use, a simple webapp for Covasim has been developed, based on Vue.js (for the frontend), ScirisWeb (for communicating between the frontend and the backend), Flask (for running the backend), and Gunicorn/NGINX (for running the server); this webapp is available at app.covasim.org. A screenshot of the user interface is shown in Figure 7. A pre-built version of Covasim, including the webapp, is also available on Docker Hub (hub.docker.com)
Covasim webapp user interface; screenshot taken from app.covasim.org.
2.7.2 Software tests
Covasim includes an extensive suite of both integration tests and unit tests; code coverage for version 1.0 is 94% (including compiled Numba functions), with much of the remaining 6% consisting of exceptions that are not raised by standard usage. In addition, outputs from the default simulations for each version are compared against cached values in the repository; since random seeds are stored, results are exactly reproducible despite the stochasticity in the model. When new data become available and parameter values are updated, previous parameters are stored, ensuring that any changes affecting the model outputs are intentional, and that previous versions can be easily retrieved and compared against.
3 Example usage
Applications of Covasim to specific settings and explorations of real-world scenarios are beyond the scope of this paper. Instead, this section provides illustrative examples of the types of analyses and outputs that Covasim can produce.
3.1. Single runs and standard features
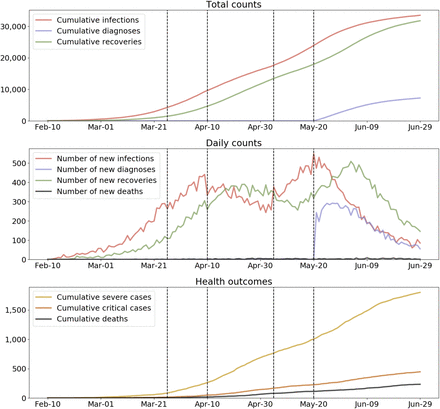
Several of Covasim’s standard features are illustrated by Figure 8. It represents a “calibrated” simulation (in terms of using a customized value of β) of 200,000 people, from February 10th until June 29th, starting with 75 seed infections. After an initial 45 days of uncontrolled epidemic spread, the following interventions are applied:: March 26th, close schools and reduce work and community contacts to 70% of their original values; April 10th, reduce work and community to 30% of their original values; May 5th, reopen work and community to 80% of their original values; May 20th, begin testing 10% of people with COVID-like illness each day, and trace the contacts of people who test positive.
Illustrative example of a single run of a Covasim simulation. Interventions (described in the text) are shown as dashed vertical lines.
By default, Covasim shows time series for key cumulative counts, daily counts, and health outcomes (including deaths). All plotting outputs are configurable, and results can also be saved in Excel, JSON, or NumPy formats for further processing. While a full Covasim application would likely include additional complexity regarding calibration and plotting, other aspects of the example shown in Figure 8 are comparable to a real-world exploratory policy analysis. Despite this, the Python script used to generate Figure 8 is only 28 lines; this code is listed in Figure 9.
Full listing of the code used to produce Figure 8, including defining the parameters of the simulation (lines 4-11); defining the interventions (lines 14-23); and creating, running, and plotting the simulation (lines 26-28).
3.2. Multiple runs and calibration
In addition to running single simulations, Covasim also allows the user to run multiple simulations, which can be averaged over to determine forecast intervals. By default, the forecast intervals used correspond to the 10th and 90th percentiles of the simulated trajectories. Although these forecast intervals bear some similarities to confidence or credible intervals, since they are typically produced through a combination of stochastic variability and parameter uncertainty, they do not have a rigorous statistical interpretation.
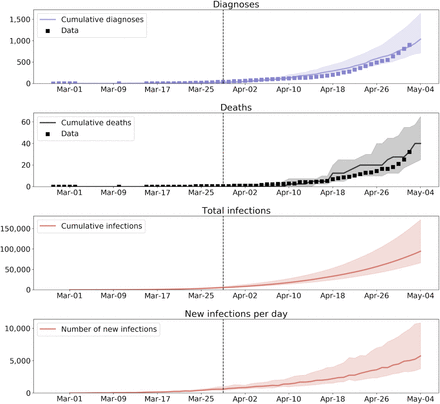
An example calibration to publicly available data from Lagos State, Nigeria, is shown in Figure 10. Assuming accurate reporting of deaths, we estimate that there were approximately 74,000 [80% forecast interval: 35,000, 120,000] people infected with COVID-19 in Lagos State by May 4th. In this example, calibration was performed using four parameters: (1) the overall transmissibility (which in the best-fit simulation was 0.0125, roughly 15% lower than the default value); (2) the number of infections already present in the population on March 1st (best-fit value, 200; note that the first official COVID-19 diagnosis in Lagos was only three days prior to that, on February 27th); (3) the per-day probability of a person with active COVID-19 symptoms being tested (best fit value, 0.4%); and (4) the change in transmission rates following the March 30th lockdown (best fit value, 50%).
Model calibration to Lagos State over the first 65 days of the epidemic, assuming accurate reporting of deaths. The dotted line indicates the beginning of the Lagos State lockdown.
3.3. Extended analyses
The preceding examples illustrate some aspects of Covasim’s core functionality that are used in most applications. However, more in-depth analyses are possible, leveraging the large number of default outputs, and the fact that the full state of the model is accessible to the user at every timestep via custom intervention functions.
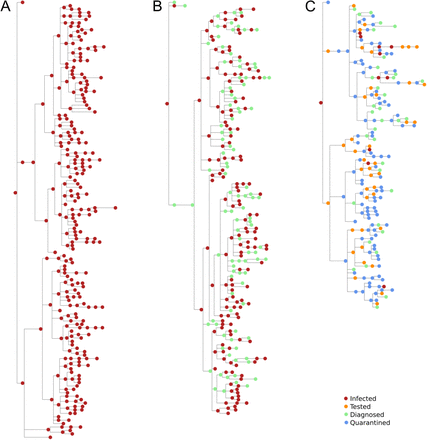
For example, detailed information about the transmission tree is stored for each simulation. This information can be used to determine the detailed microstructure of the infection patterns in a given simulation. Complete transmission trees for a small network under three different intervention scenarios are shown in Figure 11, visualized via the ETE Toolkit (Huerta-Cepas et al., 2016). For realistically sized networks, it is not feasible to visualize entire transmission trees. However, their statistical properties can be analyzed to determine transmission routes and potential intervention targets. For example, such information can be used to determine the net contribution of schools (or even teachers at schools) to the overall epidemic trajectory.
Example transmission trees for a hypothetical population of 300 individuals with a single seed infection on day 1, with (A) no interventions, (B) testing only, and (C) testing plus contact tracing. Time is represented on the horizontal axis, with each tree representing a period of approximately 90 days. The vertical size of each tree is proportional to the total number of infections.
4 Discussion
The COVID-19 pandemic has presented an unprecedented challenge to the disease modeling community in terms of requiring rapid, accurate predictions, often based on extremely limited data, with consequences of global scale. Covasim was developed to help policymakers make decisions based on the best available data, while taking into account the large uncertainties that remain in terms of COVID-19 transmission dynamics, disease progression, and other aspects of its biology, such as the proportion of asymptomatic and presymptomatic transmission.
Covasim has already been used to explore a number of different national and subnational COVID-19 epidemic projection and intervention questions, including: the impacts of school reopenings in the United Kingdom, fever screening in Nigeria, and partial workplace and community reopening in Australia; epidemic projections for Eswatini, Oregon, Colorado, and Washington; and transmission patterns aboard navy ships and cruise ships. Forthcoming publications will describe these in detail.
4.1 Limitations
Covasim is subject to the usual limitations of mathematical models, most notably constraints around the degree of realism that can be captured. For example, human contact patterns are intractably complex, and the algorithms that Covasim uses to approximate these are necessarily quite simplified.
Like all models, the quality of the outputs depends on the quality of the inputs, and many of the parameters on which Covasim relies are still subject to large uncertainties. Most critically, the proportion of asymptomatics and their relative transmission intensity, and the proportion of presymptomatic transmission, strongly affect the number of tests required in order to achieve workable COVID-19 suppression via testing-based interventions.
Dynamical models are commonly validated by comparing their projections against data on what actually happened. However, there are several challenges in using this approach for COVID-19, including (a) data quality issues (such as low case detection rates and under-reporting of deaths), (b) the difficulty of predicting future social and political responses that would significantly impact model projections (such as the timing of school and workplace reopening), and (c) the fact that model-based projections themselves have the potential to influence policy decisions, e.g., optimistic model projections may lead to relaxed policies, which in turn will lead to worse outcomes than predicted; pessimistic model projections may lead to stricter policies, which in turn will lead to better outcomes than predicted.
4.2 Future directions
Our understanding of the COVID-19 pandemic is still evolving rapidly. As additional data become available, parameter values will be continually updated. Increased data availability will also allow the incorporation of more detailed populations and networks, including aged care facilities, healthcare workers, different types of industry, spatial mixing patterns, and the socioeconomic and racial disparities present in both transmission patterns and health outcomes. A second key area of development is increased detail in modeling health system capacity, health system interventions, and treatment outcomes. Future work will also involve expansion to other locations for which sufficient data are available, with emphasis on exploring scenarios for achieving COVID-19 suppression via testing, contact tracing, and quarantine.
Data Availability
All data and source code are available; details are available in the manuscript.
Author contributions
Covasim model development was led by CCK, RMS, RGA, and DJK, with additional support by GH, KR, PS, RCN, LG, and MJ. The SynthPops model was developed by DM, with additional support by CCK, RGA, DJK, and LG. The health systems component was based on a model developed by BH. Literature and code reviews were performed by CCK, RMS, RGA, DM, GH, KR, PS, RCN, LG, APO, DD, CB, BW, SC, JPG, JAC, APO, EW, MF, and DJK. Schematics were produced by DM and MI. The manuscript was primarily written by CCK, RMS, DM, GH, PS, and DJK.
Acknowledgements
Numerous colleagues and collaborators have made generous contributions to the Covasim model and this manuscript, including: from the Institute for Disease Modeling, Dennis Chao, Charles Eliot, Christian Wiswell, Mary Fisher, Jennifer Schripsema, Clinton Collins, Christopher Jones, Christopher Lorton, Svetlana Titova, Dejan Lukacevic, Jeffrey Steinkraus, John Sheppard, Robert Hart, Guillaume Chabot-Couture, Caitlin Bever, Helen Olsen, and Natalia Corona; from GitHub, including William Fitzgerald, Hamel Husain, Cory Gwin, Julian Nadeau, Rasmus Wriedt Larsen, Aditya Sharad, and Oege de Moor; from Microsoft, including William Chen, Scott Ayers, and Rolf Harms; from the Burnet Institute, including Nick Scott and Sherrie Kelly; and from the Jet Propulsion Laboratory, Casey Handmer. We also wish to thank the participants of the Covasim Users Group, including David P. Wilson from the Bill and Melinda Gates Foundation; Andre Lin Ouedraogo from the Institute for Disease Modeling; and Julie Maher, Dean Sidelinger, and Erik Everson from the Oregon Health Authority. Institutional support, including high-performance computing resources and library access, was provided by the Burnet Institute and the University of Sydney School of Physics. This work was supported by Bill and Melinda Gates through the Global Good Fund.