Abstract
Repurposed drugs that are immediately available and have a good safety profile constitute a first line of defense against new viral infections. Despite a limited antiviral activity against SARS-CoV-2, several drugs serve as candidates for application, not only in infected individuals but also as prophylaxis to prevent infection establishment. Here we use a stochastic model to describe the early phase of a viral infection. We find that the critical efficacy needed to block viral establishment is typically above 80%. This value can be improved by combination therapy. Below the critical efficacy, establishment can still sometimes be prevented; for that purpose, drugs blocking viral entry into target cells (or equivalently enhancing viral clearance) are more effective than drugs reducing viral production or enhancing infected cell death. When a viral infection cannot be prevented because of high exposure or low drug efficacy, antivirals can still delay the time to reach detectable viral loads from 4 days when untreated to up to 30 days. This delay flattens the within-host viral dynamic curve, and possibly reduces transmission and symptom severity. These results suggest that antiviral prophylaxis, even with reduced efficacy, could be efficiently used to prevent or alleviate infection in people at high risk. It could thus be an important component of the strategy to combat the SARS-CoV-2 pandemic in the months or years to come.
1 Introduction
The novel coronavirus SARS-CoV-2 rapidly spread around the globe in early 2020 (Li et al., 2020; Zhu et al., 2020; Lai et al., 2020; Chinazzi et al., 2020). As of May 6th, more than 3.5 million cases and 250,000 associated deaths have been detected worldwide. SARS-CoV-2 causes substantial morbidity and mortality with 5% to 47% of cases requiring hospitalization (Verity et al., 2020; Cereda et al., 2020) and a case fatality ratio of the order of 1% overall, but much higher in the elderly (Wu et al., 2020; Hauser et al., 2020; Verity et al., 2020). With a short doubling time of 2 to 7 days when uncontrolled (Li et al., 2020; Cereda et al., 2020; Muniz-Rodriguez et al., 2020), this epidemic can rapidly overburden healthcare systems (Ferguson et al., 2020). Many countries have imposed social distancing measures to reduce incidence. Lifting these measures while keeping the epidemic in check may require a combination of intensive testing, social isolation of positive cases, efficient contact tracing and isolation of contacts (Bi et al., 2020; Ferretti et al., 2020). Even if these measures are locally successful in keeping the disease at low prevalence, the presence of SARS-CoV-2 in many countries and substantial pre-symptomatic transmission (Tindale et al., 2020; Ferretti et al., 2020) suggest that the virus may continue to circulate in the years to come.
Existing antiviral therapies can be repurposed to treat COVID-19 in infected individuals (Harrison, 2020; Li and Clercq, 2020; Gordon et al., 2020). Clinical trials to test several agents are underway, but existing antivirals have limited efficacy against SARS-CoV-2 and are most efficient to reduce viremia when taken early in infection (Gonçalves et al., 2020; Kim et al., 2020). Prophylactic therapy using repurposed antivirals has recently been proposed (Jiang et al., 2020; Pagliano et al., 2020; Spinelli et al., 2020). Prophylactic therapy is successfully used in the prevention of HIV infection and malaria (Mermin et al., 2006; Baeten et al., 2012). It could be an essential tool to reduce the probability of SARS-CoV-2 infection in the elderly (especially those in nursing homes), individuals with co-morbidities, and health care workers, thus substantially reducing the burden on health care systems. Depending on the safety profile of the antiviral drug it could be taken continuously (pre-exposure) or just after potential exposure (post-exposure). In this study, we integrate recent knowledge on SARS-CoV-2 host-pathogen interactions and the pharmacological properties of the antivirals currently tested in clinical trials to evaluate the efficacy of prophylactic antiviral therapy. We calculate the probability of establishment of a viral inoculum in an individual under prophylactic antiviral therapy.
2 Within-host model of viral dynamics
We consider a stochastic analog of a standard target-cell-limited model for viral kinetics. In this model, the virus, V, infects epithelial cells of the host, denoted T, with rate β. Following an eclipse phase of mean duration 1/k, cells become productively infected and virions are continuously released with rate p. Free virions and infected cells are lost with rate c and δ, respectively. A potential early humoral immune response would contribute to the clearance parameter c. When the number of cells and virions are large, the following set of differential equations describes the dynamics:
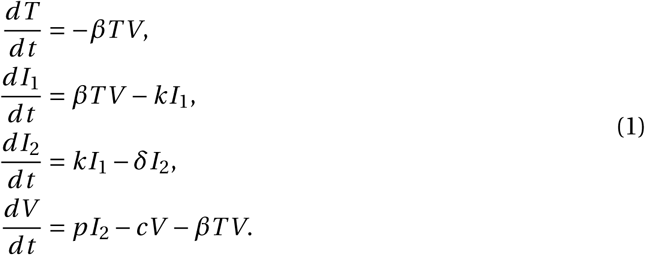
Using the same methodology as in (Gonçalves et al., 2020) to generate parameter estimates for the system in (1), we show examples of predictions in four patients (Fig. 1); (see Gonçalves et al., 2020) or Section S7 in the Supplementary Information (SI) for details. An important quantity in determining the dynamics of this model is the intra-host basic reproductive number R0. It reflects the mean number of cell infections that occur from a single infected cell at the beginning of the infection, when target cells are not limiting. Using next-generation tools for invasion analysis (Hurford et al., 2010), the basic reproductive number for the model described in (1) is given by
 where T0 is the initial number of target cells. R0 is the product of two terms: βT0/(c + βT0) corresponds to the probability that the virus infects a cell before it is cleared, and p/δ, which is the mean number of virus particles produced by an infected cell during its lifespan. We call this mean number of produced virions, p/δ, the “burst size” and denote it by N.
where T0 is the initial number of target cells. R0 is the product of two terms: βT0/(c + βT0) corresponds to the probability that the virus infects a cell before it is cleared, and p/δ, which is the mean number of virus particles produced by an infected cell during its lifespan. We call this mean number of produced virions, p/δ, the “burst size” and denote it by N.
Model predictions using the target cell limited model in four typical patients of Young et al. (2020), with a mean R0 of 7. Parameter values are given in Table S2 in the Supplementary Information.
We study the within-host dynamics of SARS-CoV-2 in the early stage of an infection, when the number of infected cells is small and stochastic effects are important. To do so, we define a set of reactions corresponding to the differential equations model from (1) (see Pearson et al. (2011); Conway et al. (2013) for similar models):

Because we are interested in early events, we subsequently assume that the number of target cells remains equal to T0 (see Section S1 in the SI). This is a reasonable assumption as long as the number ofvirionsis much smaller than the number of target cells (V (t) ≪ T (t)).
2.1 Parameterization of the model
We verify our theoretical predictions that are made under the assumption T = T0 by individual based simulations of system (3) where T is allowed to vary. Based on patient data from (Young et al., 2020), we estimate the intra-host basic reproductive number to be R0 = 7. The burst size for SARS-CoV-2 is unknown. Estimates of the burst size for other coronaviruses range from 10 – 100 (Robb and Bond, 1979) to 600 – 700 (Bar-On et al., 2020; Hirano et al., 1976). Due to the considerable uncertainty in this parameter, we ran simulations both with N ≈ 20 (parameter set ‘LowN’) and with a much higher burst size of N = 200 (parameter set ‘HighN’), which approximately corresponds to a ten-fold increase compared to the LowN parameter set. The LowN parameter set is motivated by the parameter estimation in (Gonçalves et al., 2020) adapted to our model. Details are provided in the SI, Section S7. The exact values of both parameter sets are given in Table 1. Variations of R0 are explored in the SI, Section S8.
The other parameters are not changed between the simulations and are set to: k = 5 d−1, δ = 0.58 d−1, c = 10 d−1, β = 7.403 × 10−7 d−1. The low burst size parameter set (LowN) is estimated by the same methods as used in (Gonçalves et al., 2020) but with the system of differential equations as stated in (1) – see also Section S7 in the SI. The high burst size parameter set (HighN) was obtained by fixing the burst size to 200 (a ten-fold increase compared with the reference parameter set) and inferring the value of T0 while maintaining the same R0.
3 Survival and establishment of the virus within the host
As shown in (Pearson et al., 2011; Conway et al., 2013), the probability that a viral inoculum of size V0 establishes an infection within the host is given by:
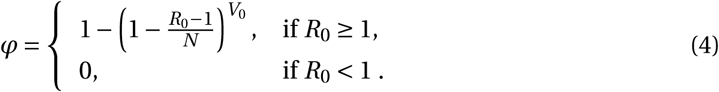
When R0 > 1, the establishment probability increases with the size of the inoculum V0. Indeed, for infection to succeed, only a single virus particle among V0 needs to establish, so the more viruses there are initially, the more likely it is that at least one establishes. Importantly, for a given R0, the virus establishes more easily when it has a low burst size N. Indeed, keeping the mean number of offspring R0 constant, a virus with a smaller burst size will have a larger infectivity β or smaller clearance c (i.e. increases the first factor of R0, see (2)). Moreover, for the same number of virions to be produced at lower burst sizes, more cells need to be involved in viral production than for large burst sizes. This mitigates two risks incurred by the virus: the risk that it does not find a cell to infect before it is cleared, and the risk that infected cells die early by chance. Since more cells are involved in viral production for lower burst sizes, these risks are shared over all these virus-producing cells. This reduces the stochastic variance in viral production, which in turn results in a higher establishment probability.
4 Prophylactic antiviral therapy blocks establishment of the virus
Next, we investigate the effect of prophylactic antiviral drug therapy on the establishment probability of the virus during the early phase of an infection. In particular, we examine drugs with four distinct modes of action: (i) reducing the ability of the virus to infect cells β, (ii) increasing the clearance of the virus c, (iii) reducing viral production p, and (iv) increasing infected cell death δ. The first mode of action corresponds for instance to drugs that block viral entry by interacting with the target cell, e.g. hydroxychloroquine, or by binding to the spike glycoprotein, e.g. a neutralizing antibody (Li and Clercq, 2020). The second mode of action models antibodies that may be non-neutralizing but which bind to circulating virus particles and facilitate their clearance by phagocytic cells. The third mode of action corresponds for example to nucleoside analogues that prevent viral RNA replication (favipiravir, remdesivir), or to protease inhibitors (lopinavir/ritonavir) (Li and Clercq, 2020). The fourth mode of action would model the effect of SARS-CoV-2 specific antibodies (given as a drug) that bind to infected cells and induce antibody-dependent cellular cytoxicity or antibody-dependent cellular phagocytosis. It would also model immunomodulatory drugs that stimulate cell-mediated immune responses.
Subsequently, we will denote by εβ, εc, εp and εδ the efficacies of the antiviral drugs in targeting the viral infectivity, viral clearance, viral production and infected cell death, respectively. Their values range from 0 (no efficacy) to 1 (full suppression). We neglect variations in drug concentrations over time within the host and, to be conservative, assume a constant drug efficacy corresponding to the drug efficacy at the drug’s minimal concentration between doses.
4.1 Antiviral reducing viral infectivity
Antiviral drugs reducing viral infectivity leave the burst size N unchanged, but reduce the basic reproductive number, R0, by 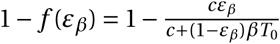 . If
. If 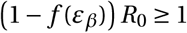 , the establishment probability changes to:
, the establishment probability changes to:
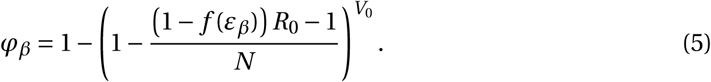
If (1 − f (εβ)) R0 is less than 1 the virus will almost surely go extinct and we have φβ = 0.
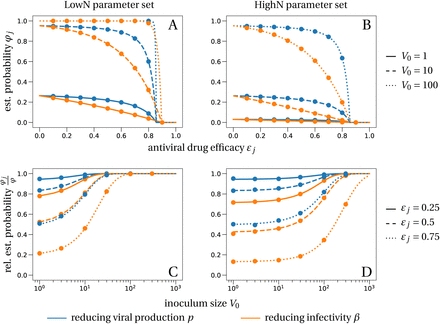
With a plausible inoculum size of 10 infectious virions (Leung et al., 2020), we find that an efficacy (εβ) of 73% (LowN parameter set) is necessary to reduce the establishment probability of a viral infection by 50% when compared to no treatment (see Fig. 2 panels A and C). Subsequently, when we mention the efficacy of an antiviral drug reducing viral infectivity, we always refer to εβ and not f (εβ).
Establishment probability of the virus under different antiviral drugs, efficacies and various inoculum sizes V0.
The lines in panels A and C correspond to the theoretical establishment probability under the assumption that target cell numbers are constant, adapted to the two modes of action (reducing viral infectivity (5) in orange and reducing viral production (6) in blue). The lines in the bottom panels represent the relative probability of establishment normalized by the establishment probability in the absence of treatment from (4), i.e. φj/φ. The theoretical predictions align well with the averages obtained from 100,000 individual based simulation of the within-host model described in system (3), in which target cell numbers are allowed to vary. Parameter values are given in Table 1.
4.2 Antiviral increasing viral clearance
Antiviral drugs that increase the clearance of extracellular virus particles reduce the average lifespan of a virus by a factor (1 − εc). This changes the clearance parameter c by a factor 1/(1 − εc). For εc = 0, the clearance rate remains unchanged; for εc = 1, virus particles are immediately cleared from the system. This reduces the reproductive number R0 by the same factor as a drug reducing infectivity: 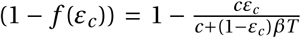 . This is an effect of our definition of efficacy. In our model, a fully efficacious drug will inhibit viral reproduction by fully suppressing the pathway it is targeting. For an antiviral drug targeting clearance, 100% efficacy means that free virions will be immediately cleared, so that no virus particle will infect a cell. This has the same effect as an antiviral drug reducing viral infectivity. The establishment probabilities therefore take the same form so that φc = φβ. Consequently, we will reduce our analysis to antiviral drugs that reduce viral infectivity, keeping in mind that results for the establishment probability are equally valid for drugs increasing viral clearance.
. This is an effect of our definition of efficacy. In our model, a fully efficacious drug will inhibit viral reproduction by fully suppressing the pathway it is targeting. For an antiviral drug targeting clearance, 100% efficacy means that free virions will be immediately cleared, so that no virus particle will infect a cell. This has the same effect as an antiviral drug reducing viral infectivity. The establishment probabilities therefore take the same form so that φc = φβ. Consequently, we will reduce our analysis to antiviral drugs that reduce viral infectivity, keeping in mind that results for the establishment probability are equally valid for drugs increasing viral clearance.
4.3 Antiviral reducing viral production
Antiviral drugs reducing the viral production (parameter p) reduce the burst size N by a factor (1 − εp). The basic reproductive number R0 is reduced by the same factor ((2)). If (1 − εp)R0 ≥ 1, such drugs alter the establishment probability as:

A reduction of 50% of the establishment probability compared to no treatment can be achieved with an efficacy of 82% (LowN parameter set, V0 = 10). The efficacy needed is greater than that for antivirals targeting infectivity or viral clearance (73%) (see Fig. 2 panels A and C). Thus, for imperfect drugs that do not totally prevent establishment, drugs targeting infectivity (or clearance) are more efficient than those targeting viral production. This effect emerges from the stochastic dynamics and the reduction in viral production variance mentioned above: in the early phase, it is more important for the virus to infect many host cells than to ensure the production of a large number of virions.
4.4 Antiviral increasing infected cell death
Increasing the rate of death of infected cells reduces the average lifespan by a factor (1 − εδ). This has the same effect on the burst size (and consequently on R0) as an antiviral drug reducing viral production, again due to our definition of efficacy. Therefore, the establishment probabilities are the same, φp = φδ. In our subsequent analysis of establishment probabilities, we thus exclusively study antivirals affecting viral production.
4.5 Critical efficacy
Above a critical treatment efficacy, the establishment of a viral infection is not possible. This is true for all modes of action and for high and low burst sizes (Fig. 2). The critical efficacy does not depend on the initial inoculum size. It is given by the condition R0 = 1, the limit when the viral population cannot grow in the deterministic model. Computing the critical efficacies for both modes of action with (5) and (6), we find:
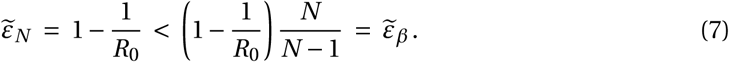
They differ for the two modes of action because reducing infectivity does not proportionally reduce R0 ((2)). Thus, drugs that reduce viral production result in a slightly lower critical efficacy, an effect that is small at low burst size and not discernible at high burst size (see Fig. 2). For example, in the LowN parameter set, we find a critical efficacy of 86% for drugs targeting viral production and 90% for drugs reducing viral infectivity.
In summary, in the range where drugs cannot totally prevent infection, drugs that target viral infectivity reduce the probability of establishment more strongly; drugs that reduce viral production can totally prevent infection at slightly lower efficacy, but this difference is extremely small when burst sizes are large.
5 Combination therapy
We analyze how the combination of two antiviral therapies could further impede establishment of the virus. We assume that two drugs that target different mechanisms of action lead to multiplicative effects on R0. The establishment probability and critical efficacies for the two drugs can be computed in the same way as for single drug treatments.
For example, a combination of two drugs reducing viral production p and infectivity β changes the establishment probability to
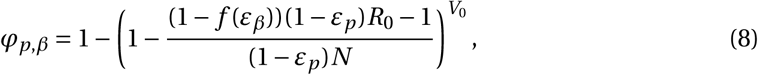 if (1 − f (εβ))(1 − εp)R0 ≥ 1.
if (1 − f (εβ))(1 − εp)R0 ≥ 1.
The corresponding critical pair of efficacies that prevent viral infection entirely can be computed as before by solving
 where the solution for
where the solution for 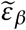 is given as a function of
is given as a function of 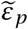 or vice versa. By the arguments from above we can replace εβ by εc and εp by εδ without changing the results. Similar calculations allow us to derive the analogous quantities if we combine drugs targeting the same mechanism of action, e.g. altering p and δ or c and β at the same time.
or vice versa. By the arguments from above we can replace εβ by εc and εp by εδ without changing the results. Similar calculations allow us to derive the analogous quantities if we combine drugs targeting the same mechanism of action, e.g. altering p and δ or c and β at the same time.
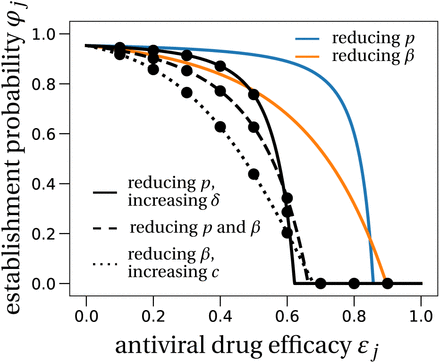
Using two drugs of limited efficacy in combination can largely reduce the establishment probability compared to the single or no treatment scenarios. For instance, two drugs with efficacies of 60% each reduce the establishment probability to 20 − 35% of the no treatment result, depending on the combination used (LowN parameter set, V0 = 10, Fig. 3). For comparison, a single drug with 60% efficacy can maximally reduce the establishment probability to ~ 70% of the no-treatment establishment probability (see Fig. 2A). We also find that, compared to the single drug cases, the critical efficacy is significantly reduced in all combinations studied.
The effect of prophylactic combination therapy on the establishment probability.
We compare different combination therapies (black lines) with the two single effect therapies (colored lines). The theoretical predictions for the combination therapies are variations of (8), adapted to the specific pair of modes of action considered. We assume that both modes of action are suppressed with the same efficacy, shown on the x-axis as εj. Dots are averages from 100,000 stochastic simulations using the LowN parameter set and V0 = 10. In Section S4 in the SI we study the effect of combination therapy in the HighN parameter set which overall leads to very similar results.
6 Time to detectable viral load and extinction time
Lastly, we quantify the timescales of viral establishment and extinction. If the virus establishes, we ask whether therapy slows down its spread and investigate how long it takes for the infection to reach the polymerase chain reaction (PCR) test detection threshold. Conversely, if the viral infection does not establish, we examine how long it takes for antiviral therapy to clear the virus. We study three drug modes of action: drugs that increase the infected cell death rate δ, and drugs reducing either viral production p or the infectivity β. Drugs promoting viral clearance c result in the same timescales as drugs reducing infectivity in the parameter set studied here (Section S5 in the SI).
6.1 Time to detectable viral load
Even if antivirals are not efficacious enough to prevent establishment of the infection, could they still mitigate the infection? We study the effect of antiviral therapy on the time to reach a detectable viral load within the host. For example, the detection threshold in (Young et al., 2020) is at 101.84 copies per mL. Assuming that the upper respiratory tract has a volume of about 30mL (Gonçalves et al., 2020), this corresponds to approximately 2,000 virus particles.
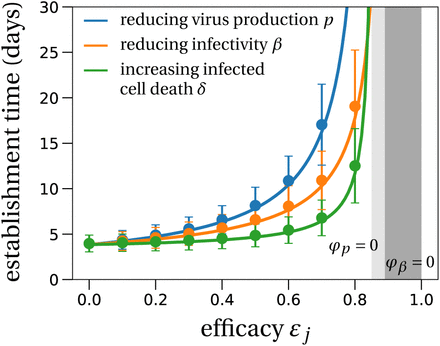
Without treatment, the viral population size reaches 2, 000 within four days (Fig. 4). Antiviral drugs can delay this time considerably. If establishment is likely, it is best to take antiviral drugs reducing the viral production p to delay the establishment of a viral infection as long as possible. This would reduce the peak viral load, which is presumably correlated with the severity of SARS-CoV-2 infection (Zheng et al., 2020). The time to reach a detectable viral load depends on the growth rate of the viral population, which is to the leading order 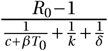 (see Section S6 in the SI for a derivation and (Bonhoeffer et al., 1997) for a similar result). The denominator is the average duration of a virus life cycle given by the sum of the phase when viruses are in the medium, the eclipse phase of infected cells, and the phase during which infected cells produce virions until their death.
(see Section S6 in the SI for a derivation and (Bonhoeffer et al., 1997) for a similar result). The denominator is the average duration of a virus life cycle given by the sum of the phase when viruses are in the medium, the eclipse phase of infected cells, and the phase during which infected cells produce virions until their death.
The mean time to reach a detectable viral load at the infection site.
Solid lines represent the theoretical prediction of the average time for the viral infection to arrive at 2,000 virions (see Section S6 in the SI for details). The light grey region depicts the parameter combinations where establishment is completely prevented by an antiviral drug reducing the burst size N (or a drug that increases infected cell death), i.e. φp = 0. The analogous region for an antiviral drug reducing viral infectivity (parameter β), i.e. φβ = 0, is colored in dark grey. We used the LowN parameter set to simulate 10,000 stochastic simulations that reached a viral load of 2,000 virus particles when starting with a single virus particle (V0 = 10). Dots are the average times calculated from these simulations, error bars represent approximately 95% of the simulated establishment times (mean ±2× standard deviation).
Importantly, the time to reach a detectable viral load is the earliest time when a patient should be tested to determine if therapy succeeded or failed to prevent infection. That time can be more than 30 days for drugs inhibiting viral production p (blue line in Fig. 4). Drugs reducing viral infectivity β also result in significant delays of 10 – 15 days in the time to establishment (orange line in Fig. 4). In contrast, drugs increasing the infected cell death rate δ do not delay the establishment timing much especially when they have low efficacy.
6.2 Extinction time
Extinction happens over a few days to weeks depending on the drug’s mode of action (Table 2). In Section S5 in the SI, we give an approximation for the distribution of the extinction time. We find that antiviral drugs that either reduce viral infectivity β or increase infected cell death δ show comparably low extinction times (Table 2). The extinction time is useful to determine the number of days a potentially infected person should take antiviral medication post-exposure. It is particularly relevant when the time to reach a detectable threshold is so long that treatment risks to be stopped before reliable detection of the virus is possible. For example in the LowN parameter set, with an antiviral drug reducing viral production p with 75% efficacy, the time to reach a detectable viral load is around 24 days on average (Table 2; V0 = 10). Yet, extinction, if it occurs, happens very quickly: the median extinction time is two days but can be longer than six days in 10% of individuals.
Establishment probabilities, extinction time statistics and establishment times for various sets of antiviral treatment. The first value in each cell gives the establishment probability, the second value denotes the median of the time to detection (days), the numbers in brackets are the 10 and 90-percentiles of the time to detection distribution (days), and the last line of numbers gives the median time to extinction (days) with the 10 and 90-percentiles in brackets. All times are rounded to half-day values if below 5 days, and to days if above. Missing values, denoted by dashes, are explained by the viral population either not going extinct or not to establish. Times which are larger than a month are just given as > 30. All values are estimated from 100,000 stochastic simulations for the establishment probability and 10,000 stochastic trajectories for the extinction and establishment times. The parameter sets for the lower and higher values of R0 are given in Table S3 in the SI.
7 Discussion and Conclusion
We propose that repurposed antiviral treatments can be used for prophylaxis to block infection by SARS-CoV-2. Using a stochastic model of within-host SARS-CoV-2 dynamics whose structure and parameters are informed by recent data (Gonçalves et al., 2020; Kim et al., 2020), we showed that in principle a combination of two drugs each with efficacy between 60% and 70% will almost certainly prevent infection (Fig. 3). For single drug treatment, we find that even intermediate efficacies can largely delay the within host establishment of the viral infection (Fig. 4). More generally, our stochastic model for the early phase of virus establishment within a host could be used to study the impact of prophylactic treatment on viral infections whose dynamics can be captured by the deterministic model in (1). A limitation of our model is that it encompasses a simplified version of events in which the effects of the innate immune responses are embedded in the parameter values of the model. For example, an early innate response, if not effectively subverted by the virus, might put some target cells into an antiviral state where they are refractory to infection, thus effectively reducing β (or equivalently, increasing c) (e.g. Pawelek et al., 2012). We neglect a potential adaptive immune response against the virus because we are interested in the early stages of the infection before the immune system develops a specific response to the viral infection. A specific immune response may in later stages enhance the ability of the body to eliminate the virus. Thus, the estimates of the drug efficacies needed to prevent establishment of infection are conservative and in reality may be overestimates. Further, even if the drugs being used do not have efficacies high enough to prevent infection on their own, they can lengthen the time needed to establish infection and hence allow time for the immune response to develop and assist in the clearance of the virus.
Our results on critical efficacy do not depend on the viral inoculum size, and correspond to a low burst size, which is the worst case scenario, in terms of infection prevention, according to (4). However, they depend on the intra-host basic reproduction number estimated at R0 = 7. This basic reproduction number was estimated from time series of viral load in 13 infected patients (Gonçalves et al., 2020). There are three main sources of uncertainty in that number, based on longitudinal viral load measurements in nasopharyngeal swabs (Young et al., 2020) and consistent with other results (Pan et al., 2020; Wölfel et al., 2020a). First, the number of virions may vary at different sites. Here we model the early phase of the infection in the upper respiratory tract, and neglect other compartments that may be more favorable to viral multiplication. For example, the number of virions in the sputum is 10 to 100 fold higher than in throat swabs (Pan et al., 2020). The upper respiratory tract may allow a small amount of virus to enter the lower respiratory tract. Modelling such complexities is difficult with current data, but would affect the establishment probability. Second, a fraction of the virions detected by a PCR assay may not be infectious (Wölfel et al., 2020b). Taking into account non-infectious virions would not change the model dynamics much but may affect the inference of parameter values on which our analysis builds. Third, the incubation time of all patients was assumed to be five days (Gonçalves et al., 2020). Varation in this value changes the timing of the peak viral load. Lower incubation times result in an earlier peak which increases the estimate of R0. Integrating fully these sources of uncertainty would require re-inferring parameter values based on corrected viral load time series and for different incubation times. While we cannot account for the first two uncertainties, we varied the incubation time from two to ten days. The corresponding parameter sets, with R0 values of 12.2 and 4.3, respectively, are analyzed in Section S8 in the SI. Our qualitative findings on the effectiveness of prophylactic therapy remain valid under these variations of R0 (see Fig. S6 in the SI). Of course, the quantitative predictions, which depend on R0, will change (Table 2). Considering the current uncertainty in the basic reproduction number and other parameters, we developed an online interactive application to compute and visualize the establishment probability and deterministic dynamics as a function of parameters. This application can be used to update our results as our knowledge of intra-host dynamics and treatment efficacies progresses (currently accessible at fdebarre.shinyapps.io/prophyiactic_antivirai_therapy). Lastly, we note that we measured efficacy as the degree of inhibition of a specific pathway (viral infectivity or production). As a consequence, drugs targeting for instance viral infectivity or production do not affect the basic reproductive number R0 in the same way. If for example the efficacies were defined such that they reduce R0 equally, critical efficacies would be the same for all modes of action.
Antiviral therapy with efficacy above a critical value can prevent infection entirely. The critical efficacies found in our stochastic model are obtained by solving R0 = 1 for different types of treatment. Solving this equation is equivalent to studying the critical efficacy in a deterministic modeling framework. However, the shape of the establishment probability can only be inferred by a stochastic analysis of the model. Below critical efficacy, drugs reducing infectivity or increasing viral clearance reduce the establishment probability the most. Importantly, drugs reducing viral production need to be close to critical efficacy to cause a marked reduction on the probability of establishment (Figs. 2 and 3).
The establishment probability increases with the size of the initial inoculum (Fig. 2). The number of virions of seasonal coronavirus in droplets and aerosol particles exhaled during 30 minutes could be in the range of 1 to 100 (Leung et al., 2020). The fact that infections are probably initiated by small numbers of viruses (a fraction of them only being infectious) justifies the stochastic analysis and explains why in most cases establishment of a viral infection is not ensured even with low-efficacy drugs.
If the inoculum size and drug efficacy are such that the virus almost always gets extinct, for how long should prophylactic treatment be taken to ensure that the virus indeed gets extinct? The answer to that question is strongly affected by the mode of action of the drug. When the drug is very efficacious and the initial inoculum is relatively large, antiviral drugs increasing infected cell death are best to quickly eradicate the virus within the host. With other drugs, however, full extinction could occur only after weeks or up to a month (Table 2, Fig. S3 in the SI).
If on the other hand, the delay between exposure and therapy and the available drug efficacy are such that establishment of the viral infection is almost certain, antiviral drugs that reduce viral production (parameter p) will slow down the exponential growth and flatten the within-host epidemic curve the most (Fig. 4). Repurposed antiviral drugs reducing viral production were recently proposed as good medication candidates against SARS-CoV-2 (Gordon et al., 2020). This prolonged period at low viral loads could give the immune system the necessary time to activate a specific response to the virus and develop temporary host-immunity against SARS-CoV-2. This might be especially important in groups that are frequently exposed to the virus, like for example health care workers.
Conclusion
Clinical trials are underway to test the efficacy of several antiviral drugs (Harrison, 2020; Li and Clercq, 2020; Belhadi et al., 2020; Sheahan et al., 2020; Maisonnasse et al., 2020), including lopinavir/ritonavir, (hydroxy) chloroquine, and remdesivir. The efficacy of these drugs is in a 20-70% range (Gonçalves et al., 2020). Thus, drugs at the high end of this interval could successfully be used in a prophylactic regime. More precise estimates of R0 and N will be available soon. The drug efficacy needed to block infection with these refined parameter estimates can be calculated with our online interactive tool, provided that viral within-host dynamics are correctly described by the model in (1). To the best of our current knowledge, prophylactic antiviral therapy can block (or at least delay) a viral infection, could be administered to people at risk such as health care workers, and alleviate the burden on the healthcare systems caused by the SARS-CoV-2 pandemic.
Data Availability
The codes and data to generate the figures are publicly available on a gitlab repository as stated in the manuscript.
Material and Methods
Simulations
The individual based simulations are encoded in C++ using the (standard) stochastic simulation algorithm for the reactions described in system (3). The code and the data used to generate the figures are available at: gitlab.com/pczuppon/virus_establishment.
Estimates for the establishment probabilities (depicted by dots in Figs. 2 and 3) are averages of 100,000 independent runs. Estimates for the time to reach a detectable viral load are obtained from 10,000 ‘successful’ stochastic simulations, i.e. 10,000 surviving trajectories. In the stochastic simulation algorithm, the viral infection is labeled as established once the number of virus particles exceeds 1,000 individuals. The time to detectable viral load was simulated with a threshold of 2,000 virions.
Acknowledgements
PC. has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement PolyPath 844369. The study received financial support of the national research agency (ANR) through the ANR-Flash calls for COVID-19 (TheraCoV ANR-20-C0VI-0018). O.T. and F.B. received funding from Grant Equipe Fondation pour la Recherche Médicale EQU201903007848. F.B. received funding from the Centre National de la Recherche Scientifique (Momentum grant). F.D. received funding from the national research agency (ANR) through the grant ANR-19-CE45-0009-01. Portions of this work were done under the auspices of the US Department of Energy under Contract 89233218CNA000001 (A.S.P.). This work was also supported by the Los Alamos National Laboratory LDRD program (A.S.P.). We are grateful to the INRA MIGALE bioinformatics facility (MIGALE, INRA, 2018. Migale bioinformatics Facility, doi: 10.15454/1.5572390655343293E12) for providing computational resources.