Abstract
The ongoing pandemic of SARS-CoV-2, a novel coronavirus, caused over 3 million reported cases of coronavirus disease 2019 (COVID-19) and 200,000 reported deaths between December 2019 and April 20201. Cases and deaths will increase as the virus continues its global march outward. In the absence of effective pharmaceutical interventions or a vaccine, wide-spread virological screening is required to inform where restrictive isolation measures should be targeted and when they can be lifted2–6. However, limitations on testing capacity have restricted the ability of governments and institutions to identify individual clinical cases, appropriately measure community prevalence, and mitigate transmission. Group testing offers a way to increase efficiency, by combining samples and testing a small number of pools7–9. Here, we evaluate the effectiveness of group testing designs for individual identification or prevalence estimation of SARS-CoV-2 infection when testing capacity is limited. To do this, we developed mathematical models for epidemic spread, incorporating empirically measured individual-level viral kinetics to simulate changing viral loads in a large population over the course of an epidemic. We used these to construct representative populations and assess pooling strategies for community screening, accounting for variability in viral load samples, dilution effects, changing prevalence and resource constraints. We confirmed our group testing framework through pooled tests on de-identified human nasopharyngeal specimens with viral loads representative of the larger population. We show that group testing designs can both accurately estimate overall prevalence using a small number of measurements and substantially increase the identification rate of infected individuals in resource-limited settings.
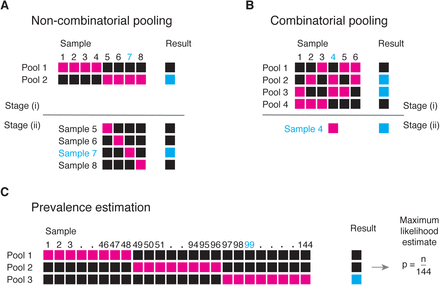
We aimed to evaluate the effectiveness of group testing for overall prevalence estimation and individual case identification. In the classical version of the identification problem7, samples from multiple individuals are combined and tested as a single pool (Fig. 1a). If the test is negative (which might be likely if the prevalence is low and the pool is not too large), then each of the individuals is assumed to have been negative. If the test is positive, it is assumed that at least one individual in the pool was positive; each of the pooled samples is then tested individually. This strategy leverages the low frequency of cases which would otherwise cause substantial inefficiency, as the majority of pools will test negative when prevalence is low. The simple pooling method can be expanded to combinatorial pooling (each sample represented in multiple pools) for direct sample identification8,9 (Fig. 1b) and to pooled testing for prevalence estimation10,11 (Fig. 1c).
In group testing, multiple samples are pooled and tests are run on one or more pools. The results of these tests can be used for identification of positive samples (A, B) or to estimate prevalence (C). (A) In the simplest design for sample identification, samples are partitioned into non-overlapping pools (magenta boxes). In stage (i) of testing, a negative result (Pool 1) indicates each sample in that pool was negative (Samples 1-4), while a positive result (Pool 2) indicates at least one sample in the pool was positive. These putatively positive samples (Samples 5-8) are subsequently individually tested in stage (ii) to identify positive results (Sample 7). (B) In a combinatorial design, samples are included in multiple pools. Putatively positive samples are those that were not included in any negative test (Sample 4). (C) In prevalence estimation, samples are partitioned into pools, and the (quantitative) results from each pool are used to estimate the fraction of samples that would have tested positive, had they been tested individually.
To deploy group testing in the current pandemic, we need designs that can account for the (i) prevalence of infection within the population, (ii) position along the epidemic curve, and (iii) within-host kinetics of viral infection. These designs should also be optimized for the use case: individual case identification (Fig. 1a,b) or overall prevalence estimation (Fig. 1c). Accounting for the within-host kinetics is important because during the course of an infection an individual’s viral load can vary by at least 6 orders of magnitude12–14 and this, along with the prevalence of infection will affect sensitivity to detect a positive sample once diluted in a pool. The position along the epidemic curve when the samples are collected (i.e., epidemic growth versus decline) is important because the population distribution of viral titers among those who are positive might (non-intuitively) vary depending on the stage of the epidemic. For example, during early phases, rapid growth of the epidemic implies that positive individuals are more likely to have been infected more recently, such that viral titers likely capture the viral growth phase. The contrast is true on the downside of the epidemic, where an increasing number of individuals will be in the recovery (low virus titer) stage of infection. The importance of this bias depends both on the epidemic growth rate and the relative duration of the within-host viral growth and waning phases.
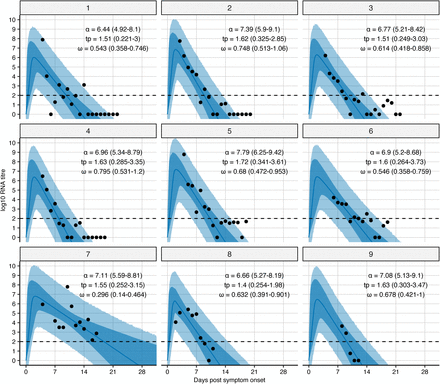
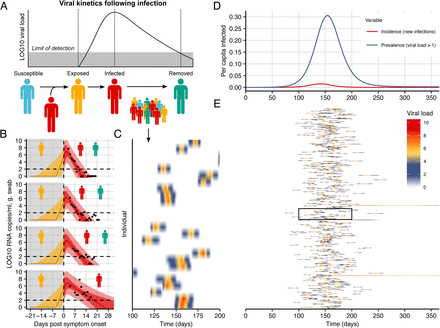
To explore optimal pooling strategies synthetically, we developed a population level mathematical model of SARS-CoV-2 transmission that incorporates realistic within-host virus kinetics (Fig. 2, Methods). We fit the model to published time-series viral load data14 to capture the variation of peak viral loads, delays from symptom onset to peak, virus decay rates and incubation periods (Fig. 2b, Extended Data Fig. 1, and Extended Data Table 1). We simulated infection prevalence under an epidemic growth and decay process, using a deterministic Susceptible-Exposed-Infected-Removed (SEIR) model of infection dynamics with parameters that reflect the natural history of SARS-CoV-2 (Fig. 2d, Extended Data Fig. 2, and Extended Data Table 1, Methods). For each simulated infection, an incubation period and virus titers over time were drawn at random from representative distributions of incubation periods15 and virus titer kinetics using the parameter fits for viral load over time described above. From these simulations, we generated a contrived realistic population of individuals, each with time-varying viral loads on each day of the outbreak (Fig. 2c,e) and used these to evaluate optimal group testing strategies in a simulated epidemic.
Note that data were extracted from (Wolfel et al. 2020). The black dots show observed log10 RNA copies/ml; solid lines show posterior median estimates; dark shaded regions show 95% credible intervals (CI) on model-predicted latent viral loads; light shaded regions show 95% CI on simulated viral loads with added observation noise. The horizontal dashed line shows the limit of detection. Inset text shows posterior median and 95% credible intervals for each of the fitted parameters. Note that these are the same fits/trajectories as in Fig 1, but with log10 viral loads assumed to start at 0 at the time of infection rather than the time of simulated infection. Because we are only inferring parameters post symptom onset (delay from symptom onset to peak viral load, peak viral load and waning rate), this change does not affect our estimates.
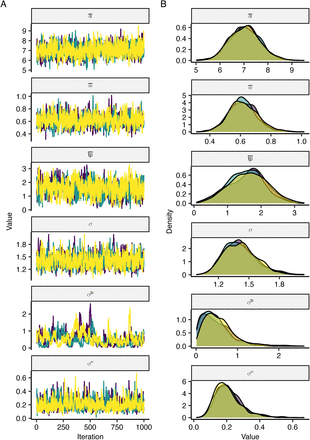
Each color shows an independent chain. (A) Trace plots showing the path of the Markov chain Monte Carlo sampler, demonstrating convergence to the same stationary distribution for all chains. (B) Estimated posterior distributions.
(A) Schematic of the viral kinetics and infection model. Individuals begin susceptible with no viral load, acquire the virus from another infectious individual (exposed), experience an increase in viral load and possibly develop symptoms (infected), and finally either recover following viral waning or die (removed). This process is simulated for many individuals. (B) Model fits to time-varying viral loads from 4 of the 9 individuals from the model fitting. The black dots show observed log10 RNA copies/ml; solid lines show posterior median estimates; dark shaded regions show 95% credible intervals (CI) on model-predicted latent viral loads; light shaded regions show 95% CI on simulated viral loads with added observation noise. The orange region shows viral loads before symptom onset (not included in model fitting), red region shows time after symptom onset (included in model fitting). The horizontal dashed line shows the limit of detection. (C) 25 simulated viral loads over time. The heatmap shows the viral load in each individual over time. (D) Simulated infection incidence and prevalence of virologically positive individuals from the SEIR model (Methods). Incidence was defined as the number of new infections per day divided by the population size. Prevalence was defined as the number of individuals with viral load > 1 (log10 viral load > 0) in the population divided by the population size. (F) As in (C), but for 500 individuals. The distribution of viral loads reflects the increase and subsequent decline of prevalence. We simulated from inferred distributions for the viral load parameters, thereby propagating substantial individual-level variability through the simulations.
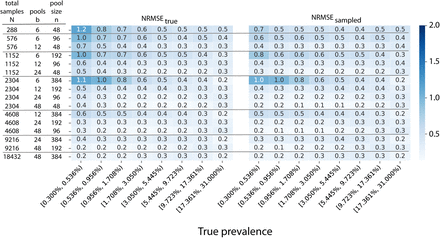
We first evaluated prevalence estimation with a range of possible pooling designs. We varied the pool size (n) of combined specimens (n=48, 96, 192, or 384) and the number of pools (b) to be evaluated (b=6, 12, 24, or 48), and (knowing the true simulated prevalence) estimated prevalence from pooled tests on random samples of individuals drawn during epidemic growth (days 20-150) and decline (days 150-300) phases of the epidemic (Methods).
Our results (Fig. 3) demonstrate it is possible to obtain accurate estimates of prevalence over at least four orders of magnitude, with up to 400-times less testing. For example, we find that a population prevalence study that collects 9,216 samples can very accurately capture the true prevalence of infection by performing only 48 PCR tests (b = 48 pools of n = 192 samples each) and that this accuracy holds for a wide range of true prevalences from 0.005% to 30% (Fig. 3b; Extended Data Fig. 3). As expected, the total number (N) of samples collected was important for accurate estimates depending on true prevalence. Specifically, estimates were most accurate when N is greater than one divided by prevalence (Fig. 3a). When this condition is not met, the estimates perform somewhat better in capturing the prevalence represented within the samples themselves, but we find that error in representative sampling may drive discrepancies away from the true population prevalence (Fig. 3c and Extended Data Fig. 3). For all values of N, partitioning the samples into more pools improves accuracy when N is greater than one divided by prevalence (see multiple rows with the same values for N in Fig. 3b,c and Extended Data Fig. 3). Thus, we find that with a sufficiently large number of total samples collected, very accurate estimates of prevalence can be measured using a small fraction of tests than would be needed in the absence of pooling.
Normalized root mean squared error (NRMSE, 
; greyscale and text in each box) between estimated prevalence and true prevalence (left) or between estimated prevalence and sampled prevalence (right) is shown for a variety of pooling designs (individual rows). Prevalence range shown in individual columns.
In prevalence estimation, a total of N individuals are sampled and partitioned into b pools (with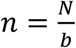 
samples per pool). The true prevalence in the entire population (x-axis in A; individual columns for prevalence ranges in B and C) varies over time with epidemic spread of viral infections. In (A), the prevalence in the sampled population (y-axis; red line depicts average, red shaded region is one standard deviation over 100 random trials at each point in time) and estimated prevalence (y-axis; blue line and shaded region) are plotted against true prevalence for three different pooling designs. (B and C) Normalized root mean squared error (NRMSE, 
; color and text in each box) between estimated prevalence and true prevalence (in B) or between estimated prevalence and sampled prevalence (in C) is shown for a variety of pooling designs (individual rows).
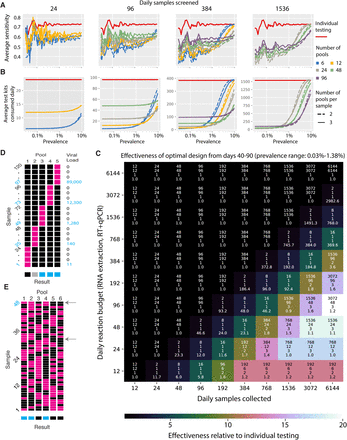
We next analyzed the effectiveness of group testing for determination of individual sample results (Fig. 1a,b). Because positive samples are diluted in a pool, usually with many negatives, we might intuit that the sensitivity of the assay would be reduced. However, it is worth noting that this is not always the case because a feature of pooled testing is that a sample that becomes diluted below the LOD may nonetheless be identified (‘rescued’) if the pools containing that sample also include at least one other sample that is sufficiently above the LOD. Based on our models of viral kinetics, we estimate the sensitivity of conventional (non-pooled) PCR testing to be ~70% (i.e., 30% of the time we sample an infected individual who has a viral load greater than 1 but below the LOD; here 100 viral copies per mL, Fig. 4a). This reflects a combination of either sampling during the incubation period of the virus (i.e., after infection but prior to the onset of symptoms) as well as a relatively long duration of low viral titers during viral clearance (Fig. 2b, Extended Data Fig. 1). In addition to affecting sensitivity, prevalence impacts testing efficiency. Here, we define testing efficiency as the total number of samples tested divided by the total number of tests performed. If there are no positive results, the total number of tests will be equal to the number of pools. As prevalence increases, testing efficiency will decrease because the number of tests needed to be performed in order to resolve exactly which samples are positive will increase.
Using a fixed population of 500,000 simulated individuals, a variety of group testing designs for sample identification (Supplementary Table 2) were evaluated on the basis of sensitivity (A), efficiency (B), and overall effectiveness in identifying positive samples relative to individual testing (C). (A and B) The average sensitivity (A, y-axis) and average number of tests needed to identify individual positive samples (B, y-axis) using different pooling designs (individual lines) were measured over days 40-120 in our simulated population, with results plotted against prevalence (x-axis, log-scale). Results show the average of 2,500 trials, with individuals selected at random on each day in each trial (fluctuations at low prevalence reflect random effects in the small number of infected individuals in fixed population at early times). Pooling designs are separated by the number of samples tested on a daily basis (individual panels); the number of pools (color); and the number of pools into which each sample is split (dashed versus solid line). Solid red line indicates results for individual testing. (C) Every design was evaluated under a pair of constraints on number of samples collected on a daily basis (columns) and number of reactions that can be run on a daily basis (rows) over days 40-90. Text in each box indicates the optimal design for a given set of constraints (arranged vertically: number of samples, number of pools, number of pools into which each sample is split, average number of times this design is run on a daily basis given the constraints). Color indicates the average number of positive samples identified on a daily basis using the optimal design, relative to the number of positive samples identified through individual testing with the same constraints. (D, E) Pooled testing of samples was validated experimentally. (D) Five pools (columns of matrix), each consisting of 24 nasopharyngeal swab samples (rows of matrix; 23 negative samples per pool and 1 positive, with viral load indicated in teal on right) were tested by viral extraction and RT+qPCR. Pooled results indicated as: negative (black), inconclusive (grey), or positive (teal). (E) Six combinatorial pools (columns) of 48 samples (rows; 47 negative and 1 positive with viral load of 12,300) were tested as above. Pools 1, 2, and 4 tested positive. Arrows indicate two samples that were in pools 1, 2, and 4: sample 32 (negative), and sample 48 (positive).
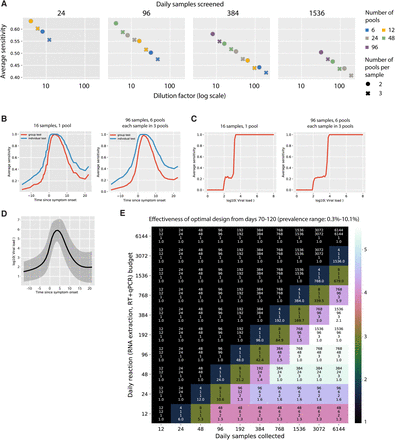
We used our simulated epidemic to generate contrived samples collected over time to estimate how both sensitivity and testing efficiency are affected by the number of pools and number of samples in each pool, throughout the course of the epidemic. We refer to the number of samples divided by the number of samples in each pool as the dilution factor. (Extended Data Fig. 4a, see Methods for a full description of the underlying group testing simulations).
(A) The sensitivity (y-axis) of different designs (individual points) is plotted against the dilution factor of each design (x-axis, log scale). Pooling designs are separated by the number of samples tested on a daily basis (individual panels); the number of pools (color); and the number of pools into which each sample is split (circle versus cross). (B) The sensitivity (y-axis) of two pooling designs (two panels; design indicated above plot) for individual case identification is plotted against time relative to onset of symptoms (x-axis). Red lines: sensitivity with the indicated group testing design; Blue lines: sensitivity with individual testing. (C) As in (B) with the same two pooling designs, but with sensitivity plotted as a function of viral load in our simulations (x-axis; log scale). (D) The mean (solid line) and standard deviation (shaded region) of viral load (y-axis, log scale) relative to the onset of symptoms (x-axis) in all positive samples in the simulated population. (E) Every design was evaluated under a pair of constraints on number of samples collected on a daily basis (columns) and number of reactions that can be run on a daily basis (rows) over days 70-120. Text in each box indicates the optimal design for a given set of constraints (arranged vertically: number of samples, number of pools, number of pools into which each sample is split, average number of times this design is run on a daily basis given the constraints). Color indicates the average number of positive samples identified on a daily basis using the optimal design, relative to the number of positive samples identified through individual testing with the same constraints.
Our simulations show how sensitivity is affected by both prevalence and the dilution factor. At early times in the epidemic, prevalence is low and sensitivity is decreased relative to individual testing for all pooling designs due to dilution. When prevalence is high (>10%), sensitivity of group testing approaches the sensitivity of individual testing as lower viral load samples are ‘rescued’ by higher viral load samples (Fig. 4a). Several aspects of the pooling design contribute to the decrease in sensitivity at earlier times. First, when more samples are tested, the dilution factor has the potential to be bigger. Second, for a given number of samples, the dilution factor will generally be larger when the number of pools is smaller. Third, for a given number of samples and pools, the dilution factor is bigger when each sample is split into more pools. Each of these effects is borne out in our results (Fig. 4a, Extended Data Fig. 4a), with sensitivity decreasing roughly linearly as the log of the dilution factor (Extended Data Fig. 4a). Importantly though, these lower sensitivities are due to failure to identify samples with low viral load (Extended Data Fig. 4b,c,d). Because viral titers peak early after viral infection while virus clearance is associated with a relatively long duration of low virus counts potentially for weeks afterwards (Extended Data Fig. 4b,d), the loss in sensitivity stems from a failure to detect low viral load specimens that might be less clinically relevant. The benefits gained, in terms of testing efficiency, must therefore be weighed against the loss in sensitivity, both for surveillance and with an eye towards the clinical importance of missing low viral load specimens.
Testing efficiency is partly determined by the number of pools, and partly determined by the prevalence of infection. When prevalence is low, efficiency is roughly the number of samples divided by the number of pools, since there are rarely putative positives to test in the validation stage (Fig. 4b). However, for any given pooling design, the number of test kits consumed on a daily basis will increase over time as the number of positive samples in the population grows. There are two aspects of the pooling design that mediate the increase in consumed tests. The first and most significant is that, for a given number of samples tested on a daily basis, the number of test kits consumed per day will increase more quickly when there are fewer pools (see different colored lines in Fig. 4b). This is because there will be more putative positives for the same number of true positives when the number of pools is small. For example, when there is only one pool, every sample is a putative positive and must be re-tested if the pool tests positive, whereas with several pools, if only a subset of pools tests positive, then only a subset of samples needs to be re-tested (Fig. 1a,b). For the same reason, with a given number of samples and pools, when each individual sample is split into fewer pools, the total number of tests will increase more quickly (dashed versus solid lines in Fig. 4b).
Thus, there are tradeoffs to consider between sensitivity and efficiency: testing more samples will potentially result in lower sensitivity but greater efficiency; having more pools will result in greater sensitivity and lower efficiency when prevalence is low, but higher efficiency when prevalence is high; and, splitting each sample into more pools results in lower sensitivity but greater efficiency. The appropriate balance between these may depend on the goal at hand.
In a setting of community screening, we may be ultimately interested in total recall (the total number of positive individuals that we are able to identify). While individual testing may have the highest sensitivity (because samples are not diluted), with limited resources it might be that individual testing identifies fewer positive samples than group testing, because fewer samples are being screened.
To systematically explore total recall in resource limited settings, we evaluated results averaged over days 40-90 (up to a prevalence of 1.3%, when most designs begin to rapidly lose efficiency; Fig. 4b) for individual testing and a wide array of group designs (Extended Data Table 2), under a variety of “budget” constraints on the number of samples collected daily, and the number of reactions that can be run on a daily basis. Across all constraints considered, effectiveness (total recall relative to individual testing) of the optimal design ranges from 1 (when testing every sample individually is optimal) to 20 (i.e., identifying 20x more positive samples on a daily basis compared with individual testing with the same budget). Examining the effectiveness of the design achieving the greatest total recall under each combination of budget constraints (Fig. 4c), shows that when sample collection is limiting, samples should always be screened individually (matching our intuitive understanding). When sample collection is in excess of reaction capacity, group testing becomes more effective, with single pool designs being most effective when samples are in slight excess (2-8x), and combinatorial designs being most effective when there is a large excess of samples relative to reaction capacity (see trends within rows as the number of samples increases in Fig. 4c). When prevalence is higher (e.g., over days 70-120, with prevalence from 0.3% to 10%) the optimal designs shift more towards combinatorial pooling and the overall effectiveness is reduced (up to 5.5x more effective than individual testing; Extended Data Fig. 4e).
Finally, we performed two pilot lab experiments for group testing of SARS-CoV-2. First, we assessed if testing pooled samples of variable viral loads behaves as expected with respect to dilution effects. Beginning with 5 nasopharyngeal clinical swab samples with previously determined viral loads (11, 140, 1,280, 12,300, and 89,000 viral copies per ml), we diluted each at equal volumes into 23 negative nasopharyngeal swab samples (dilution factor of 24), then extracted viral RNA and ran RT-qPCR on each pool (Methods). The results were consistent with a (diluted) LOD of 10: the first pool was negative, the second inconclusive (negative on N1, positive on N2), and the remaining three all positive (Fig. 4d, Extended Data Table 3). Next, we tested combinatorial pooling. Starting with 48 samples (47 negative and 1 positive with a viral load of 12,300) we created 6 pools, with each sample split into 3 pools (Fig. 4e, Extended Data Table 4, Methods). As anticipated, 3 pools tested positive and 3 negative, with the 3 positive pools corresponding to those including the single positive sample (Fig. 4e, Extended Data Table 5). One negative sample was included in the same 3 pools as the positive sample; thus, 8 total tests (6 pools + 2 validations) were needed to identify the single positive sample out of the 48.
Taken together, our results suggest that group testing for SARS-CoV-2 can be a highly effective tool for community screening. Our analysis suggests that a few dozen tests can be used to accurately infer prevalence, and we identify an array of designs for sample identification that optimize the rate at which infected individuals are identified under constraints on sample collection and reaction throughput. While our experimental tests suggest it might be possible to translate these results into practice, there are several reasons why theoretically optimized group testing designs might be limited in the practical context of SARS-CoV-2 epidemiology. First and foremost, there is little point in group testing when sample collection is limiting, as it has been during the current outbreak in some regions of the world due to limited availability of nasopharyngeal swabs. Moreover, even when swabs are not limiting and more samples could be collected, substantial logistical challenges in managing and tracking thousands of samples (potentially in multiple pools) must be overcome. In addition, while we assume that individuals are sampled from the population at random in our analysis, in practice samples that are processed together were also typically collected together. Substantial coordination will therefore be necessary to make group testing practical, but investing in these efforts could enable community screening where it is currently infeasible, and provide epidemiological insights that are urgently needed.
Data Availability
Raw data generated in this study are available in Extended Data Tables 3 and 5.
Author contributions
B.C. and J.H. performed the simulations and modeling. B.B. performed the pooled testing. B.C., J.H, A.R, and M.M. analyzed results and wrote the manuscript with input from all authors.
Competing interests
A.R. is a co-founder and equity holder of Celsius Therapeutics, an equity holder in Immunitas, and an SAB member of ThermoFisher Scientific, Syros Pharmaceuticals, Asimov, and Neogene Therapeutics.
Methods
Model of infection dynamics
We implemented a deterministic compartmental model to describe the increase and subsequent decline of SARS-CoV-2 infection incidence and prevalence. The model captured the following progression: individuals begin fully susceptible to infection (S); become exposed but not yet infectious (E); become infectious (I); and are finally removed (R). Our aim was to capture changes in incidence over time (increasing incidence rate before the peak and declining incidence thereafter) and the resulting population-level distribution of viral loads, and we therefore did not model additional complexity such as deaths, pre-symptomatic transmission or age-stratified outcomes. Although incorporating these mechanisms may alter the simulated epidemic dynamics for a given set of transmission parameters, we do not expect them to impact inference from the pooled testing analyses.
The model was defined by the following set of ordinary differential equations:
where β is the transmission rate, scaled to give a basic reproductive number R0 of 2.2; 1/σ is the incubation period, assumed to have a mean of 6.4 days; 1/γ is the infectious period assumed to have a mean of 7 days; and N is the population size, assumed to be 6,900,000 (the state of Massachusetts, USA). All model parameters and assumed values are described in Extended Data Table 1. Using this model, we simulated per capita daily infection probability (i.e., the daily incidence) and prevalence.
Viral load kinetics
Viral load was assumed to increase exponentially following infection, peaking soon after symptom onset, and subsequently undergoing exponential decay. These assumptions are equivalent to linear growth and decay on a log scale. The log10 viral load over time, ν(t), was given by:
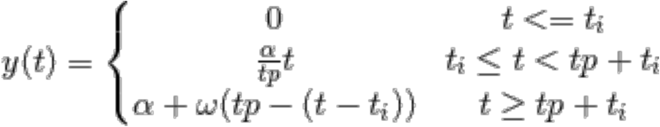where α is the peak viral load; tp is the time of peak viral load post infection; and ω is the waning rate post peak. For the purpose of simulation, tp was split into the incubation period (time from infection to symptom onset) and time from symptom onset to peak viral load.
Fitting the viral kinetics model
Time-series viral load data were obtained from a case series of 9 hospitalized COVID-19 patients from a single hospital in Munich, Germany14. These data provide regular measurements of log10 RNA copies per ml from nasal and nasopharyngeal swabs. Data were extracted using a web plot digitizer (https://automeris.io/WebPlotDigitizer/). We used a random-effects model to infer individual-level viral kinetics parameters alongside population-level distributions. Under this model, each individual had their own parameter value for peak viral load, time from symptom onset to peak and waning rate, drawn from normally distributed population-level averages with estimated means (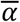
, 
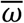and 
), and fixed or estimated standard deviations (σα σω and σtp) (Extended Data Table 1). Because all of the viral load measurements were taken after the onset of symptoms, we did not infer the timing of infection. Instead, we assumed that tp represented only the time from symptom onset to peak viral load and ti = 0. This did not affect our estimates for α, tp or ω.
The model was fit using a Markov chain Monte Carlo (MCMC) framework, using a likelihood that assumes normally distributed observation error with estimated standard deviation σobs. The likelihood function accounted for truncation at the lower limit of detection (LOD) by integrating over the left hand tail of the normal cumulative density function for model-predicted viral loads less than the LOD. All estimated parameters were given uniform priors with bounds shown in Extended Data Table 1. Individual-level viral kinetics parameters were given hyperpriors as described above. Code to regenerate the MCMC fitting is provided (see Code availability). Briefly, an adaptive Metropolis-Hastings algorithm was run for 300,000 iterations with the first 100,000 iterations discarded as burn in. Convergence was assessed visually based on trace plots of 3 independent chains (Extended Data Fig. 2). All estimates parameters had an effective sample size (ESS) greater than 200, other than σtp which had an ESS of 100.
Simulation framework
We combined the estimates from the transmission model and viral kinetics model above to simulate viral loads for a population of n individuals over time. For each individual, we simulated a time of infection (or no infection) from the time-varying probability of infection, p(t). For each infected individual, an incubation period was drawn from a log normal distribution with mean (of the natural log) = 1.57 and standard deviation (of the natural log) = 0.65 as estimated previously15. Next, we drew viral kinetics parameters for each individual from normal distributions with means of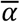 
, 
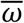and 
and standard deviations of σα, σω and σtp, respectively. Finally, we simulated the time-varying viral load of each infected individual, starting at the time of infection. These simulations provide a population of viral loads incorporating realistic variability in viral load kinetics and between-individual parameters.
Estimating prevalence from pooled test results
We adapted an inference framework developed for modeling HIV prevalence with pooled antibody tests10 to build a maximum likelihood estimate (MLE) of prevalence among N samples based on the results of b pooled tests, with each pool consisting of 
samples. Briefly, the MLE is determined by computing the conditional probability of the observed results given that there were k positive samples, and integrating over all values of k. To compute these conditional distributions, we estimate an empirical distribution of Ct values that follows from the distribution of viral loads in infected individuals. Notably, fitting empirical distributions allows our inference framework to be independent of the modeling choices made for epidemic spread and viral kinetics. The empirical distributions used here are derived from all of the simulated viral load measurements in a set of individuals selected as a training population. This is conceptually similar to using the empirical distribution of all real measurements from a population taken to date. We note that although these distributions may not be reflective of the true distribution of viral loads across the entire population on a given day (e.g., because the distributions on a given day will be different during epidemic growth or decline), we were nonetheless able to accurately infer the true underlying prevalence.
Let fk,n = P(Y|k, n) represent the conditional probability of the observed Ct values in each pool, Y = [y1,…,yb], given that there were k positive samples in the pool and n-k negative samples. Computing these distributions will be the central task of generating prevalence estimates.
To begin, we model Ct values as a function of the underlying viral loads:
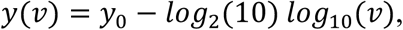where ν is the viral load (in copies per ml). To capture variance in the LOD between labs or across batches within a lab, we let the intercept, y0, be normally distributed with unknown mean and standard deviation. We assume uniform priors over each y0 (μ ~ Uniform(37,39), σ ~ Uniform(0.1,1)). These ranges and the log-linear relationship are based on a calibration of Ct values to a dilution curve of positive control SARS-CoV-2 RNA samples (data not shown), and are consistent with prior measurements calibrated to SARS coronavirus16.
fk,n depends not only on the distribution of Ct values arising from a given viral load, but also on the distribution of viral loads in infected and uninfected individuals. Here we assume that the viral load in uninfected individuals is always zero (we do, however, allow for false positive PCR results, as discussed below). Given access to the true distribution of viral loads, fk,n can be generated by the convolution of k density functions. Since we do not have access to the true distributions, we approximate fk,n through a kernel density estimate (KDE) of empirical convolutions. Specifically, for a given value of n and each value of k from 1 to n, we generate 10,000 random combinations of k viral loads,
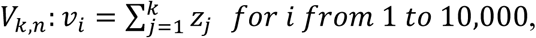where zj are the randomly sampled viral loads. For each i, we sample μ ~ Uniform(37,39), σ ~ Uniform(0.1,1) and y0 ~ N(μ,σ) and then generate Ct values:
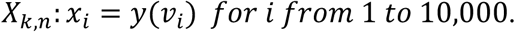
We then approximate fk,n = KDE(Xk,n) with a bandwidth parameter of 0.1.
Several adjustments to these density approximations are needed to account for false positives and undefined Ct values (i.e., undetected viral RNA). To allow for Ct values that might arise from false positives, we define f0,n = f1,n r, where r is an assumed false positive rate of PCR (here, we set r = 0.2% and allow this to be misspecified when simulating false positives below). When viral RNA is undetected and k > 1, we let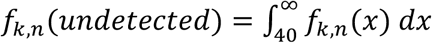 
, where a Ct value of 40 is used as a typical limit of detectable RNA. When k = 0, f0,n(undetected) = 1 − r.
Following the model of Zenios and Wein10 the MLE of prevalence, p, is defined as:
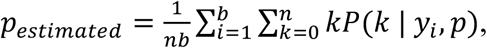where n is the number of samples per pool, b, is the number of pools, and yi is the Ct value observed in pool i. We calculate P(k | yi,p) using the conditional densities above:
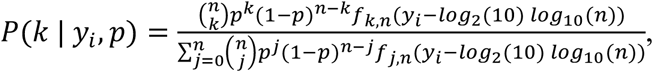substituting the appropriate values of f when the Ct value is undefined. Note that each of the observed Ct values is adjusted to account for n-fold dilution. Finally, we find pestimated through an iterative expectation-maximization algorithm, where at each iteration
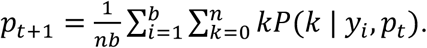
Using this model, we evaluated prevalence estimation across time in our simulated populations. We first partition the simulated population into training and testing sets. Observed viral loads in 20% of individuals (selected at random) are used to train the KDEs above. All remaining analyses are done on the testing population. We simulate viral loads in b pools of samples as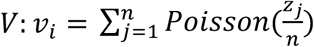 
for i from 1 to b, where Poisson sampling is used to model the sampling of a small volume from each swab. From these we simulate Ct values, Y. At each time point, we randomly select N individuals, partition them into b pools, and simulate the pooled viral loads and Ct values, Y, with y0 ~ N(38.5,1) sampled randomly in each trial and applying the transformation described previously. To capture false positive PCR results at a rate of 1%, with 1% probability in each pool we add a viral load of 
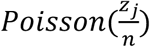, with zj selected at random from all positive samples with 
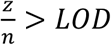on a given date. We then compute the true prevalence in the population, ptrue, the prevalence in the population of N samples, psampled, and the prevalence estimated from b tests, pestimated. To quantify accuracy we calculate the mean and standard deviation of these values at each time point across 100 random trials (Fig. 3a), and summarize differences between pestimated and either ptrue or psampled with the normalized root mean squared error (NRMSE; either 
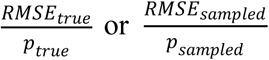; Fig. 3b,c and Extended Data Fig. 3).
Group testing for sample identification
In the classical version of group testing for sample identification, samples from multiple individuals are combined and tested as a single pool. If the test is negative (which might be likely if the frequency of positives is low and the pool is not too big), then each of the individuals is assumed to have been negative. If the test is positive, it is assumed that at least one individual in the pool was positive; each of the pooled samples is then tested individually (Fig. 1a). This strategy leverages the low frequency of cases which would otherwise cause substantial inefficiency, as the majority of pools will test negative when prevalence is low. A mathematical framework for determining optimal pooling sizes was originally applied to efficiently screen for syphilis during World War II7.
More recent applications involve combinatorial pooling strategies, where each sample is split into multiple, partially overlapping pools8,9 (Fig. 1b). Good designs ensure that each sample is represented in a unique combination of pools, where the number and composition of pools are adjusted depending on the prevalence and error rate. If there are no errors, and at most one sample in the population is positive, then the set of positive tests across the pools uniquely identifies the single positive sample (as in Fig. 1b). Such designs are typically used in non-adaptive group testing, where the goal is to exactly identify the positive samples using only results on a single round of pooled tests. In order to be able to exactly decode up to k positives in a population of N samples, the number of combinatorial pools needs to scale as 0(k2log(N))8,9 A class of matrices, called disjunct matrices, that are appropriately sized and allow for exact decoding are typically used in this context.
Here we consider a very simple form of adaptive group tests, where putative positive samples are individually tested in a validation stage. Because we perform this second stage of testing, we are not restricted to disjunct matrices (allowing for exact identification in stage (i)), and we can use fewer pools than are required for non-adaptive testing.
In this setting, a given pooling design is defined by several parameters: the total number of individuals, N; the total number of pools, b; and the number of pools, q, into which each individual sample is split (each sample will be split the same number of times—this constraint is imposed both for ease of laboratory workflow, and so that samples are treated equitably). For instance, if we have N=50 individuals with samples split randomly into q=2 out of b=4 pools, then on average, each pool would contain 25 samples, and thus be diluted 25-fold. We analyzed a large array of designs (with N between 2 and 6,144, b between 1 and 96, and q from 1 to 3; Extended Data Table 2) to understand effects on sensitivity, efficiency and total recall, and to identify optimal designs under different resource constraints.
For any given design we can simulate pooled testing results on the simulated population described above. For each time point, we randomly select N individuals from the population. Each individual is then randomly assigned to q out of b pools. For each pool, we then calculate the net sampled viral load,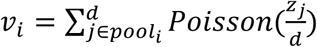 
using the viral loads zj for each individual included in pooli, where Poisson sampling is used to model a small volume sampled from each swab. If νi > LOD the pool is assigned a positive value, otherwise the pool is negative (here, with LOD=100). To allow for false positive PCR results at a rate of 1%, with probability 1% we set the result of the pool to be positive, regardless of the viral load.
Based on the results of b pooled tests and the assignments of samples to pools, we can infer putative positive samples. This is done using a simple decoding algorithm: any sample that was included in a negative test is eliminated as a negative; the remaining samples are putatively positive. This simple, yet highly effective algorithm can be easily implemented in a notebook or very simple Excel sheet.
Simulations are run by repeating the random pooling, pooled testing, and decoding procedures described above. At each point in time, 2,500 trials are run selecting N individuals at random in each trial. We then record the number of validation tests, s, in each trial, corresponding to the number of putative positive samples. Average efficiency at a point in time, t, is then calculated as A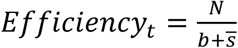
. Average sensitivity is calculated as 
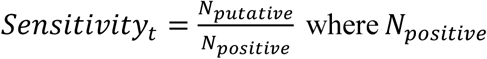where Npositive is the total number of infected individuals (viral load > 1) that were sampled across all trials and Nputative is the number of such individuals who were identified as putative positives. From these values we calculate Total Recallt = Efficiencyt Sensitivityt.
Based on these results we evaluated a large array of group testing designs (Extended Data Table 2) under a series of constraints on number of samples collected and number of reactions run per day (Fig. 4c). For a given design D: (N, b, q) we calculate the average number of tests run,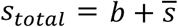 
, and the total number of times that D could be run on a daily basis, 
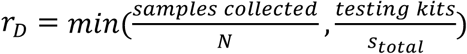. We then calculate the effective testing capacity on a daily basis, cD = N rD SensitivityD, and average this value over days 40 to 90 (Fig. 4c) or 70 to 120 (Extended Data Fig. 4e) of the simulated epidemic. Notably, when sample collection is limiting, CD = samples collected * Sensitivity(samples collected, samples collected,1), corresponding to individual testing. Finally, the optimal design for a given combination of constraints is the design with the greatest average effective testing capacity. In Fig. 4c and Extended Data Fig. 4e we show the relative effectiveness, corresponding to effective capacity relative to individual testing.
Sample collection
All samples used in this study were de-identified, discarded human nasopharyngeal specimens previously tested at the Broad Institute. Samples were pooled before RNA extraction and qPCR.
RT+qPCR of pooled samples
All pooled population samples were tested following the Broad Institute CRSP SARS-CoV-2 Real-time Reverse Transcriptase (RT)-PCR Diagnostic Assay as submitted for Emergency Use Authorization. Briefly, RNA is isolated from nasopharyngeal and oropharygneal specimens in 50ul VTM/UTM using MagMAX™-96 Viral RNA Isolation Kits (Thermo Fisher Scientific, AMB18365), performed on an Agilent Bravo Liquid Handling Platform running VWorks (Build 11.4.0.1233), and is reverse transcribed to cDNA and subsequently amplified in the Applied Biosystems® ViiA7 Real-Time PCR Instrument with QuantStudio version 1.3 software. In the process, the probe anneals to a specific target sequence located between the forward and reverse primers. During the extension phase of the PCR cycle, the 5’ nuclease activity of Taq polymerase degrades the probe, causing the reporter dye to separate from the quencher dye, generating a fluorescent signal. With each cycle, additional reporter dye molecules are cleaved from their respective probes, increasing the fluorescence intensity. Fluorescence intensity is monitored at each PCR cycle by Applied Biosystems® ViiA7 Real-Time PCR System with QuantStudio version 1.3 software. The software allows the fluorescence intensity to be monitored at each PCR cycle to allow for the qualitative detection of nucleic acid from SARS-CoV-2.
Code availability
The SEIR model, viral kinetics model and MCMC were implemented in R version 3.6.2. The remainder of the work was performed in Python version 3.7. The code used for the MCMC framework is available at: https://github.com/jameshay218/lazymcmc. All other code and data used are available at: https://github.com/cleary-lab/covid19-group-tests.
Data availability
Raw data generated in this study are available in Extended Data Tables 3 and 5.
Extended Data Tables
Values shown are posterior median estimates and 95% credible intervals or fixed values. Individual-level estimates are shown in Extended Data Fig. 1. Prior bounds show lower and upper bounds on uniform priors placed on estimated parameters when running the Markov chain Monte Carlo algorithm. Note that the upper bound on delay from symptom onset to peak viral load parameter is varied for each individual. This was taken as the first day post symptom onset for which an individual has an observation.
Five positive samples with variable viral loads (89,000, 12,300, 1,280, 140, and 11, for samples 1-5, respectively) were each pooled with 23 negative samples. Values in table show the Ct values for each of five pools for three primer pairs (N1, N2, and RP), along with a final call (positive, negative, or inconclusive).
Each of 48 samples was split in equal volume into 3 out of 6 pools. Sample 48 was positive (viral load 12,300), and all other samples were negative.
Ct values from qPCR on combinatorial pools. qPCR results for combinatorial pools in Extended Data Table 4. Values in table show the Ct values for each of six pools for three primer pairs (N1, N2, and RP), along with a final call (positive, negative, or inconclusive).
Acknowledgements
We thank Xihong Lin, Madikay Senghore, Benedicte Gnangnon, Abdul Sesay, Rounak Dey, David Hong, Edgar Doriban and Heather Shakerchi for useful discussions. Work was supported by the Merkin Institute Fellowship at the Broad Institute of MIT and Harvard (B.C.), by the National Institute of General Medical Sciences (#U54GM088558; JAH and MJM); and by an NIH DP5 grant (MJM).
References
