ABSTRACT
When actively taking measures to control an epidemic, an important indicator of success is crossing the ‘peak’ of daily new infections. The peak is a positive sign which marks the end of the exponential phase of infection spread and a transition into a phase that is a manageable. Most countries or provinces with similar but independent growth trajectories had taken drastic measures for containing the COVID-19 pandemic and are eagerly waiting to cross the peak. However, the data after many weeks of strict measures suggests that most provinces instead enter a phase where the infections are in a linear growth. While the transition out of an exponential phase is relieving, the roughly constant number of daily new infections differ widely, range from around 50 in Singapore to around 2000 just in Lombardy (Italy), and 7600 in Spain. The daily new infection rate of a region seems to depend heavily on the time point in the exponential evolution when the restrictive measures were adopted, rather than on the population of the region. It is not easy to point the critical source of these persistent infections. We attempt to interpret this data using a simple model of newer infections mediated by asymptomatic patients, which underscores the importance of actively identifying any potential leakages in the quarantine. Given the novelty of the virus, it is hard to predict too far into the future and one needs to be observant to see if a plan B is needed as a second round of interventions. So far, the peak achieved by most countries with the first round of intervention is extremely flat.
INTRODUCTION
SARS spread in around 29 countries, infecting around 8,096 individuals globally [1]. Quarantine strategies were implemented by several governments, and they were effective in reducing the number of newer infections [2]. The number of casualties from other epidemics such as Swine flu in 2009, MERS in 2015 were also similarly contained. However, the infections caused by the novel coronavirus (COVID-19) continue to increase. The World Health Organization has declared COVID-19 as a pandemic, the first one in the 21st century [3]. Since so far there is no known treatment or vaccine, after weighing the damages to the lives versus that to the economy, most governments across the world have implemented the nonpharmaceutical interventions such as strict measures of social distancing, or even lockdowns and curfews, guided by the historic response to the.
For an emerging pandemic such as COVID-19, a first natural scientific impulse is to model it via standard epidemiological models [4-5] such as the Susceptible-Infected-Recovered (SIR) model to predict how rapidly the infections can spread without an intervention or how quickly a lockdown program may be planned [6]. Governments and public health modelers are interested in understanding the effectiveness of various strategies [7-10] starting from a complete lockdown, or a reduced social contact [11] and a subsequent release of restrictions in a phased manner. Many such models have already been developed to model COVID-19, and have been guided by the past intuitions from modeling how the epidemic spread declines with changes in season or with active containment strategies, and the success of China which after 2 months of lockdown reports no new COVID-19 infection cases consistently for more than 3 weeks.
In the time of a pandemic, an important question asked on daily basis by public and policy makers is when the pandemic is going to ‘cross the peak’. Crossing the peak signifies that one may expect fewer cases of infection, compared to the previous day. It sends positive signals of pandemic containment to the people as well as to the economy and other aspects of the social life. It also indicates the time for lowering the guard is not too far. As such, a few weeks after these strict measures, and noting the reported success of China, governments of various provinces and countries are waiting for the new daily infections to cross over the peak. Because of the drastic measures, the number of daily new cases are no longer increasing in many places. However, it is worrying that they do not have clear signatures of a downward trend either. In this context, we perform a detailed analysis of the nature of this peak, and whether it has been achieved. As it turns out, most provinces and countries that implemented containment are no longer in an exponential growth phase, but rather enter a new, and possibly unexpected, linear growth phase which we discuss here.
RESULTS
Multiple hotspots make the growth multi-exponential
In the early stage of infection spread, each infected individual becomes a vector for transmission the infection. Thus, rate of increase infections can be captured by a simple model,
 where I is the number of infected individuals, R is the number of recovered individuals, P is the total population and rate of transmission is r. Specifically, with the current variant of COVID-19, where the median recovery time is 10-15 days, the exponential increase in I is always much faster than the slow growth of R. One can see from the data in the growth phase of the pandemic spread in any country that typically R < 10-15% of I, and I << P. In principle, one can also consider detailed models such as the SIR model, or even detailed agent-based models assuming a more realistic social contact structure. However, the simple phenomenological model
where I is the number of infected individuals, R is the number of recovered individuals, P is the total population and rate of transmission is r. Specifically, with the current variant of COVID-19, where the median recovery time is 10-15 days, the exponential increase in I is always much faster than the slow growth of R. One can see from the data in the growth phase of the pandemic spread in any country that typically R < 10-15% of I, and I << P. In principle, one can also consider detailed models such as the SIR model, or even detailed agent-based models assuming a more realistic social contact structure. However, the simple phenomenological model
 does capture the growth of I.
does capture the growth of I.
The number of infections in a well diffused society, community or a province would thus grow as I(t)=I0 exp(αt), where I0 is the number infections at t=0. However, the transmission across countries or less-frequented provinces, occurs much through a jump-diffusion process, with only occasional jumps over these boundaries, and a diffusion within the region. As a consequence, the trajectory of a country with two epicenters can be thought as two independent weakly interacting subsystems which leads to emergence of a multi-exponential I(t)= I0,1 exp(α1t)+ I0,2 exp(α2t) with the I0,1 and I0,2 being the number of infections in these two decoupled regions at t=0, and α1, α2 the rates in these two regions which may or may not be same depending on mobility in the cities, any other restrictions imposed by the local Governors. For administrative reasons, one may be interested in following the trajectory of the world, or of a specific country. But depending upon the lag between these multiple hotspots, the exponential nature of the growth gets masked. Thus, for detailed studies, one needs to unmask this data by decoupling these multiple exponentials and focusing on the individual provinces, which are possibly separated from other provinces by travel restrictions. After decoupling, it is clear that the different regions very similar exponential growth curves.
Decoupled data show a shift from exponential to linear growth
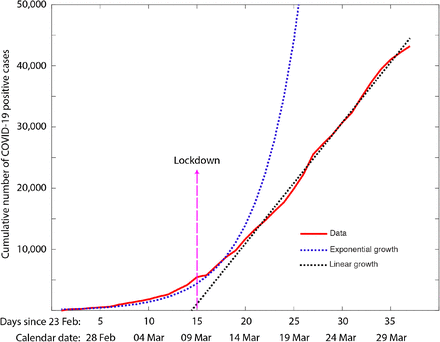
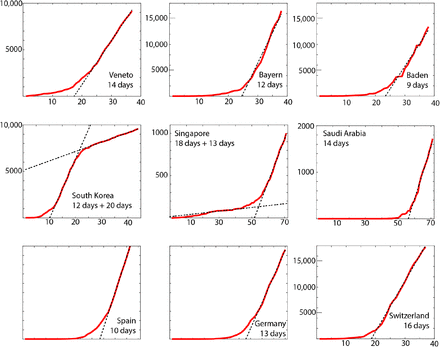
We first illustrate the qualitative change in the spread of infection using the data from the number of infected cases in Lombardy [13]. As Figure 1 shows, about a week after the lockdown, the growth in Lombardy transitioned from an exponential to a linear growth. In Figure 2, we study the growth in South Korea, Singapore, Saudi Arabia, Switzerland, Spain,[14] Germany and two of its states (Bayern, Baden) and another Italian province Venice. It is apparent from the data that the later part of the data from all these countries shows a clearly linear trend. Even the number of deaths recorded on a daily basis also show the same linear trend. Clearly a transition from the exponential regime is a relief. And this transition happens around 10 days from the day of the restrictive measure, possibly coinciding with the distribution of the incubation time.
The cumulative infections which show an exponential transition continue with an average of 1974 new COVID-19 positive cases. The date on which the lockdown was implemented is shown. Interestingly, the transition to linearity happens within around 10 days after the lockdown.
The plots show the infections by provinces or countries. As it can be seen the number of infections enters a linear regime for all these regions, and the corresponding slopes are given in Table 1. The data up to 1st of April was used in these analyses (the data from Germany and Spain is from the 3rd of April). The legends in the figures suggest that the number of days for which the growth continued in a linear regime. South Korea and Singapore have two distinct linear regimes, and the duration in both are indicated.
However, the slope of these curves, which indicate the number of new daily infections is very different for the different regions. South Korea’s response by contact tracing and extensive testing has been widely praised. Although the number of daily new cases has crossed a peak there are still an average of 100 cases every day from the 12th of March till the 3rd of April. While 100 new cases may be a manageable number in terms of resource allocation, several other countries or provinces are in a linear growth regime with much larger daily new cases: Switzerland (980), Italy (≈4200), Germany (≈5600), Spain (≈7600) despite the containment measures.
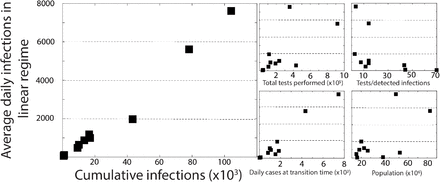
The number of daily infections is not the same for different provinces
To date, other than China which continues to report nearly zero new infected cases every day for the past few weeks, all other countries are either in an exponential phase or a linear growth phase. The daily new infected cases for the provinces and countries we analyzed in Figures 1, 2 are given in Table 1. The dependence of the daily new cases on various factors such as the extent of testing, the population of the region, etc was studied in Figure 3. A strong correlation was observed with the number of cumulative infections in the region, and the number of daily infections at the time when the containment measures were taken. Which seems to suggest that COVID-19 infections at this point are held in a pause. Looking back, if the quarantine or lockdown decision is taken later in time the average number of daily new cases would have been significantly higher. Of course, the same message applies for the future before relaxing the social restrictions that have helped contain the spread of the COVID-19.
Data showing the average number of daily new infections (slope in the linear regime) along with other relevant information for each country or province. *Estimated from the German national testing as of 1 April 2020. §The infection data from South Korea shows two different linear regimes. The first one which immediately follows the end of the exponential regime is considered. ¶Singapore also showed two linear regimes, a very short linear regime early on, followed by what appeared to be an exponential phase. However, since the absolute numbers are very low and noisy during the first linear regime in this work, the second linear regime was considered.
The slope from the linear regime was compared with several factors to see if any factor could potentially help interpret the linear regime. It is understood that all these factors are not entirely independent but some are connected. The cumulative infections and the number of daily cases around the time when the transition occurred are the most correlated. The number of tests performed per single detection is poorly correlated, and the other variables such as population of the region do not appear correlated. As much as the linear regime suggests the end of the exponential growth phase, a correlation of the daily cases with the average number of infections at the time of transition seems to suggest that the growth is only maintained in a “pause”, frozen at the state where the quarantines are implemented.
Model
There is now enough evidence that one main difference of COVID-19 has been the high rate of transmission by the asymptomatic individuals. In an attempt to model the observed transition from an exponential to a linear growth phase, we resort to simple rate equations by including A, which is the number of asymptomatic patients.


 λ is the infection rate via asymptomatic individuals, δ reflects the natural rate of reduction in the numbers of asymptomatic patients post-incubation period, β is the rate at which asymptotic individuals transmit to other individuals, ρ is the rate at which by performing tests one reduces the A by moving them to a quarantine. c is the rate of increase due to non-human sources such as aerosols or contact surfaces. We perform the simple analysis with μ=0, assuming the recovery rate is much slower than the rate of infection. A median hospitalization time of 3 weeks from the data does support this assumption, as in the exponential phase the increase in the number of infections in these 3 weeks is much higher. However, the following analysis should remain valid even if μ≠0.
λ is the infection rate via asymptomatic individuals, δ reflects the natural rate of reduction in the numbers of asymptomatic patients post-incubation period, β is the rate at which asymptotic individuals transmit to other individuals, ρ is the rate at which by performing tests one reduces the A by moving them to a quarantine. c is the rate of increase due to non-human sources such as aerosols or contact surfaces. We perform the simple analysis with μ=0, assuming the recovery rate is much slower than the rate of infection. A median hospitalization time of 3 weeks from the data does support this assumption, as in the exponential phase the increase in the number of infections in these 3 weeks is much higher. However, the following analysis should remain valid even if μ≠0.
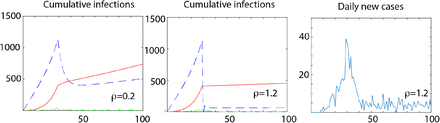
In Figure 4, we illustrate a simulation of these differential equations to show the transition to linear regime, the nature of the peak, constant rate of daily fluctuations and the reduction in the number of the daily infection rate with ρ.
The rate equations in Eq.(3) were simulated to see if the observations can be captured. The simulation was performed with parameters such as α=0.1, and the transmission via asymptomatic is individuals is much lesser with λ=0.01. At this growth stage of the pandemic since the data from most countries show a recovery rate of around 10%, we performed the simulation with μ=0. The asymptomatic (blue), and recorded infections (red) with two different testing rates ρ=0.2 and 1.2 initiated after the lockdown period (30 on axis which represents the days) are shown in panels A and B. As expected a transition from an exponential to linearity is observed. Panel C shows the daily new infections when ρ=1.2. Since the Eq.(3) is stochastic, we added an incubation period drawn randomly from a beta-distribution with a mean of 10 days. For this choice of parameters which were chosen to qualitatively emulate the peak observed in South Korea, a a low level of daily new infections persist. However, by varying ρ, it was seen that these average number of these daily new cases decreases with the ρ and increases with the time of lockdown (data not shown).
In Eq. 3a, the dependence of dI/dt on I is the main reason for the exponential growth. A quarantine of infected individuals removes this dependence with α=0, and turns the behavior to one of linear growth. The number of asymptomatic individuals in principle will reduce to zero after a strict implementation of quarantine, followed by the decay rate of infection in the individuals. However, assuming our model is realistic, a sustained increase in infections appears to be possible only through a leakage in the quarantine program. The lowest rate of spread of I will be in the steady state dA/dt=0, when
 where γ‘ is the growth in A, due to a leakage from I. Since the measures are already in place, this will be a weak coupling. As long as A≠0, the cumulative number of infected individuals will continue to increase until most or all of the susceptible individuals are infected (Eq.3a), which is quite undesirable considering the scale of devastation that has already been caused to even the developed countries by roughly 1 in 500 infections. According to this model, and not too far from common sense, a significantly high rate of testing ρ and keeping a check on the potential leakage from infected individuals even under a quarantine condition can reduce the number of asymptomatic individuals.
where γ‘ is the growth in A, due to a leakage from I. Since the measures are already in place, this will be a weak coupling. As long as A≠0, the cumulative number of infected individuals will continue to increase until most or all of the susceptible individuals are infected (Eq.3a), which is quite undesirable considering the scale of devastation that has already been caused to even the developed countries by roughly 1 in 500 infections. According to this model, and not too far from common sense, a significantly high rate of testing ρ and keeping a check on the potential leakage from infected individuals even under a quarantine condition can reduce the number of asymptomatic individuals.
DISCUSSION
Observation of a linear growth phase
In this work, we note by studying the COVID-19 infection data from several countries which implemented quarantine that the exponential growth phase ends, but it is followed by a linear growth phase. A deviation from an exponential growth phase is a relief to the population, and a sign of success of the containment measures. The significance of this is that there are no new infections caused by an individual who is understood be infected. However, via indirect route or secondary effects there is a still a constant rise in the cumulative number of infections, in many places with a very high daily rate.
The peak is flat
The unmoderated peak is understood at the population level using established SIR models, when most or all of the susceptible individuals develop infections and immunity. In the first week of April, the number of global COVID-19 infections reached 1 million. The hospital resources, health care personal, economies are already overwhelmed by the pandemic, when as little as 1 in 500 are infected in many developed countries. So, at this point in this work we do not attempt to project the dates when a much higher fraction of the society is infected, or evaluate the consequences of such mass scale infection, which may also come with several other assumptions such as the reduction of the virulence upon spreading, etc. Further, the definition of who is susceptible is not yet clear. In the initial months of COVID-19 infection, people over an age of 65, and with comorbidities were considered highly susceptible. However, although at a much lower rate, one begins to hear about healthy individuals in their 20s or 30s succumbing to COVID-19. Instead, we focus on the peak that is achievable by active interventions, such as the ones SARS, MERS had seen.
A peak explained in a lay language is the time when for the first time the number of new infections are lower than the previous day crossed. However, with stochastic fluctuations on a daily basis, this statement needs to be interpreted by observing consistent trends over a few days. However, the number of daily COVID-19 infections in many places has been roughly constant, at least for 3 to 4 weeks, after containment measures. Even if eventually the new infections do decline because of any reason, it must be understood that the high number of daily infections present a strange situation of having chronic and acute severity simultaneously for at least many weeks, if not longer.
However, if instead of following the trends in the daily fluctuations, if one fits a sigmod function to the cumulative infections it can lead to confusing interpretation. Extrapolating the slowing exponential trend in the early days following the quarantine, the sigmoid will predict a peak. However, this peak will shift when the same fit is repeated in the days later, with a dominant linear component, as in reality a linear graph does not have a peak.
Asymptomatic, but contagious?
We explore the possibility that the constant rate of new infections is a false signal from the constant rate of testing. If it is indeed the case, the screening tests are showing infections of people not just asymptomatic, but asymptomatic and not contagious. If there is a way of distinguishing the latter, it must be clarified to reduce the global panic levels. However, prima facie this possibility can be refuted because although the countries such as South Korea and Singapore on the one extreme are performing extensive screening tests (43 and 70 tests on average for every detected infection), countries such as Switzerland are performing tests only when there are significant symptoms, or pre-existing vulnerabilities, and of course for health care personnel. Thus, the new infections arising purely as an artefact of over testing does not seem like a possibility.
Hope and Plan B
So far, other than China, most countries have shown only a transition from an exponential to a linear growth phase. The hope is that eventually the linearity will fade out with an exponential decay of the numbers of asymptomatic and infected individuals or at least reduce in intensity as it did in South Korea, which showed a shift from a constant daily new infections of 600 to daily new infections of 100 (the second linear regime in Figure 2). The second linear regime from South Korea thus presents an interesting case study. South Korea had ramped up its testing capacity from about 1000 per day in early February to around 10,000 per day from February 25 till at least early April. Whether the reduced number of daily infections a few weeks after this ramp up is a consequence of the tests or of any contact tracing that allowed them to test and isolate the large number of asymptomatic individuals or purely depends on the decay time of the infection in the asymptomatic individuals which was has so far been underestimated to be around 10 days needs to be understood with an in-depth analysis of the policies and implementation, which we could not perform even after parsing through the information that is publicly available.
It is clear that the availability or implementation of newer resources such as mass-immunizations, therapeutic interventions or even the chance that the SARS-COV-2 reduces in lethality due to mutations or seasonal variations were not considered in our analyses. Several other models have made the predictions of the peak of the infection at the population level. When any of these possibilities arise, it is possible to adapt those models to predict the peak for a newer country or region which still did not implement those interventions.
However, the reality today is different and none of these options at our disposal. We instead focus on how this scenario is evolving, based on the real data rather than assumptions. Whether the number of daily new infections continue at the constant but very high daily rate or decline, should be tracked from the real data rather than making a prediction based on past experiences from other infections. If this hope does not get the support of the data, each country depending upon its current overload of active infections and health care resources needs to have a “plan B”.
Presently the only two interventions available are testing and isolation. Both of these are of course qualitative in nature. How extensively to perform the tests, how restrictive and privacy-limiting should the isolation be, has been interpreted differently by different countries.
SUMMARY AND OUTLOOK
In summary, we ask three questions: Has the implementation of these strategies been successful? The answer we find is that it is. From an exponential behavior, most countries transitioned to a linear behavior showing that the infected individuals are not causing new infections. And this happened roughly around 10 days after the implementation of the social distancing or quarantine policies.
While this is a moment of triumph and many may be wondering when is a good time to lower the guard and relax the restrictions, we ask the second question: if the goal of reducing the number of daily infections below a manageable level been achieved. From the data after 3 to 4 weeks of strict measures by many countries, it has not yet reached this level. This happens because instead of a decline in the number of daily cases, they saturate, and that too at very high values (7600 in Spain, 5600 in Germany, etc).
We then raise the third question for an open interpretation, not to be restricted by the limited understanding of the authors: Why this linear regime persists for so many weeks, and would it reduce in intensity naturally or require a newer intervention such as extensive testing or prevention of unexpected leakages in the system of isolation and quarantine through health care workers, essential services or any other means we cannot imagine today. If there are indeed such leakages, these are not the ones that can be predicted by following the overall number of infections of states or countries as was done in this work, but rather by taking a detailed audit, by tracking the need and rigor of implementation in each industry and segment of the society. We analyze the data using a simple model that seems to suggest that if the linearity persists, this may be due to leakages in the quarantine system, and can be partly compensated by increasing the rate of testing. Theoretically, it is possible that the measures adopted by China were much more stringent compared to other countries which allowed a reduction in the new infections. However, given the gravity of the situation, we present our observation, analysis and model in all its humility, for an open interpretation.
The aim of this work is mainly to point to existence of this new, and at least for us, linear growth phase with a very high number of daily new infections, which brings a very hard to manage mix of acute and chronic societal burden. Given the gravity of the situation the world is facing, the data of the linear phase needs an open interpretation by all the experts. With all good intentions, we wish the slope of this linearity to be reduced in a few weeks, and the linearity shown in this work is not relevant in longer term. However, the data is not currently in favor of such wishes. Thus, to understand if the existing interventions are working one needs to detach oneself from the notion of a peak followed by a decline or even the linear phase we propose in this work and monitor the true data needs to be regularly, and make policy decisions based on the data.
Data Availability
All data will be available on request
Conflict of Interest
The authors declare no conflict of interest.
Acknowledgements
S.A and M.K.P acknowledge the support of JNCASR for this research. M.K.P acknowledges the discussions with Nadia Ambrosi and Yousung Jung which were very helpful in understanding the ground realities in Europe and South Korea. S.A. and M.K.P acknowledge Prof. K. R. Sreenivas, Dr. Sunil Sherlekar for helpful discussions.