ABSTRACT
For an emergent disease, such as Covid-19, with no past epidemiological data to guide models, modelers struggle to make predictions of the course of the epidemic (1), and when predictions were made the results would vary widely. Yet much empirical information is already contained in the data of evolving epidemiological profiles. We show, for epidemics of low fatality rate, both empirically with data, and theoretically, how the ratio of daily infected and recovered cases can be used to track and predict the course of the epidemic. Ability to predict the turning points and the epidemic’s end is of crucial importance for fighting the epidemic and planning for a return to normalcy. The accuracy of the prediction of the peaks of the epidemic is validated using data in different regions in China showing the effects of different levels of quarantine. The validated tool can be applied to other countries where Covid-19 has spread, and generally to future epidemics. A preliminary prediction for South Korea is made with limited data, with end of the epidemic as early as the second week of April, surprisingly.
SIGNIFICANCE We offer a practical tool, as an alternative to traditional models, for tracking and predicting the course of an epidemic using the daily data on the infection and recovery. This data-driven tool can predict the turning points two weeks in advance, with an accuracy of 2-3 days, validated using data from various regions in China selected to show the effects of quarantine. It also gives information on how rapid the rise and fall of the case numbers are. Although empirical, this approach has a sound theoretical foundation; the main components of the results are validated after the epidemic is near an end, as is the case for China, and therefore generally applicable to future epidemics of low fatality rate.
Introduction
The current COVID-19 epidemic is caused by a novel corona virus, designated officially as SARS-CoV-2, spreading from Wuhan, the capital city of Hubei province in China (2-4). The new virus seems to have characteristics different from SARS (severe acute respiratory syndrome) (5, 6): it is less deadly but more virulent (7-10). Modeling the epidemic as it develops has been difficult (1). Depending on the model assumptions, predictions of when it “turns a corner” varies wildly (11-21), from now or until after 650 million people have been infected before peaking in the “worst-case scenario” (22). Now as the epidemic has spread beyond China (23, 24), a reliable prediction of the course of the outbreak in each region is critical for the management and containment of the epidemic, and reducing public anxiety and panic. China has instituted some of the strictest quarantine measures around Wuhan and Hubei, which may or may not be adoptable in other countries (25-27). It would be useful to extract the dependence of the epidemic’s evolution on the degree of quarantine to guide policy decisions, while also to characterize properties of Covid-19 that are applicable to other countries.
The turning point and the end of the epidemic are the two most watched markers on its development (28, 29). There are various definitions of the turning point. A common one defines the turning point of the epidemic as the reported daily number of newly infected reaching a peak and then declining. This is the one touted in the various news announcements, and also used by some research groups (22). The fact that the number of newly infected reaching a peak and then declining does not necessarily imply that the epidemic has “turned a corner”, because the total number of still-infected can still be rising with the associated urgent need for additional medical resources, such as hospital beds and isolation wards. Furthermore, locating this peak is highly susceptible to data glitches and change in diagnostic definition. For example, on 12 February, when Hubei changed its definition of confirmed infection from the gold standard of nucleic acid gene-sequencing tests to clinical observations and radiological chest scans, over 14,000 newly infected cases were added that day, creating a peak that has not been exceeded since. Overwhelmed doctors in Wuhan pleaded for the change so that they did not have to wait for the returned tests to confirm the infection. If the definition of the turning point based on the peak of newly infected were used, it would have given 12 February as the turning point for Hubei. Outside Hubei, there was no change in definition for the “infected”.
A more meaningful turning point should be based on the number of confirmed infected individuals, designated as the Existing Infected Cases (EIC)(15), reaching a peak and then starting to decline. EIC is in theory obtainable from data of the daily number of newly infected, N(t), and the daily number of newly recovered, R(t), by subtracting the accumulated sum of R(t) from the accumulated sum of N(t). Analysis of this accumulated quantity is sensitively affected by accumulation of poorer early data of reported cases, including under-reporting and under-detection of the number of infected caused by insufficient test kits, in addition to the history of changing diagnostic criteria. Moreover in practice its peak is often not detected until several weeks after it has occurred.
Since the maximum of EIC can be located by the zero of its derivative, we propose using a local-in-time metric of N(tp)=R(tp) at the peak of EIC, tp. We demonstrate that for the ongoing COVID-19 epidemic, this determination of the turning point is not sensitive to past data problems, including the rather dramatic increase in N(t), on 12 February, when Hubei changed its definition of “confirmed infected”. Also since it uses the newest diagnostics, with the testing facilities ramped up, hopefully the numbers are more accurate.
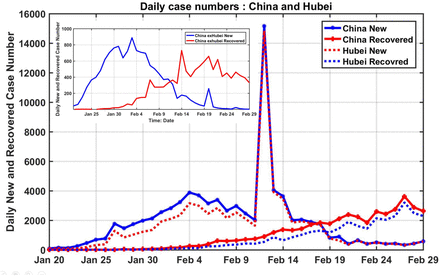
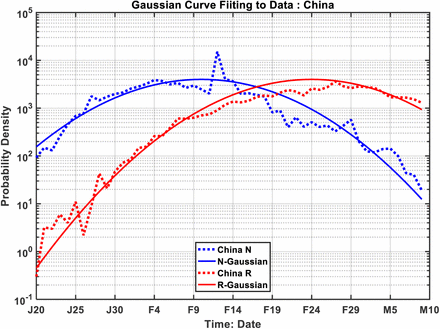
Fig. 1 shows how this turning point is empirically determined using daily time series of reported N(t) and R(t). For China as whole, tp is found to be February 18; for Hubei, the province of the epicenter Wuhan, tp is found to be 19 February, and for China outside Hubei (China exHubei), 12 February, coincidentally on the same day as the Hubei data spike. However there is no such bump in the data outside Hubei, and so is not likely the result of the data artifact. These results, even including that for Hubei, are not affected by the historical data problems because of our local-in-time method for determining the turning point.
The daily newly infected (in blue) and the daily newly recovered (in red), as a function of time for China as a whole (in solid lines) and Hubei (in dotted lines). The turning point is determined by when the red and blue curves cross. Inset For China outside Hubei.
The fact that the turning point for the epidemic in China exHubei occurred earlier than that for Hubei could reveal the effectiveness of the quarantine of Hubei. In Wuhan, with hospitals facing the number of infected far exceeding available hospital beds in the initial period, some infected patients were not adequately isolated.
Secondary and tertiary infections might have played a role in delaying the turning point. On the other hand, outside Hubei, hospitals were not as overwhelmed because of the strict quarantine placed on Hubei, which drastically reduced the import of the disease originating from Hubei. The infected were better isolated, reducing further spread, and treated in hospitals, resulting in shorter time to recovery (see Table S1).
EIC corresponds to I(t) in the traditional SIR (susceptible-infected-recovered) model(28), if deaths are not counted in R(t). Most predictions have used models similar to SIR, though some current ones are much more sophisticated (12-14, 17, 21), but they all rely on parameters, such as contact, infection rates, time between secondary and first infections, and case fatality rates. None of them are known with any certainty (1). Most model predictions of the turning point have the epicenter Hubei leading the rest of China by 1-2 weeks in its predicted turning point, the opposite of what the data show. In many SIR types of models, an epidemic would end after most people are infected and acquire immunity. These models tend to have the disease run its course sooner the earlier it started.
Can such a turning point be predicted before it happened, and if so by how many days in advance?
Determining the epidemiological characteristics
We define the N to R ratio as

At tp, NR=1.
We show in Figure 2, using the data of the epidemic for COVID-19, that the logarithm of NR(t) lies on a straight line, with small scatter, passing through the turning point tp. And data for various stages of the epidemic, from the initial exponential growth stage, to near the peak of EIC, and then past the peak, all lie on the same straight line. The intercept with logNR=0 yields the turning point. This line, obtained by linear-least-square fit in the semi-log plot, is little affected by the rather large artificial spike in the data on 12 February because of its short duration and the logarithmic value. That reporting problem is necessarily of short duration because, on the date of definition change, previous week’s cases of infected according to the new criteria were reported in one day. After that, the book is cleared, and N(t) returned to its normal range.
Logarithm of the ratio of daily newly infected to newly recovered. They lie on straight lines with some small scatter. The straight line obtained by linear-least squares fit is in dotted line. The slopes of the lines are almost the same but with different intercept; the trend lines cross zero (the black solid line) at different time for different regions indicating different peaking time for EIC. The epicenter Wuhan (green) has latest turning point than its province Hubei (pink), which has a later turning point than China as a whole (cyan).
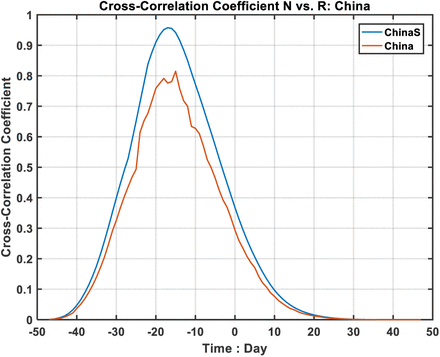
It would be interesting to understand why the empirically determined log NR(t) lies on a straight line, and what determines its slope. See Method for a theoretical support. For a disease with a low fatality rate, which COVID-19 is (30), most newly infected individuals would eventually recover after a hospital stay of T days. So R(t)∼N(t-T). This simple observation lies at the heart of our justification for the straight line for log(NR). In Figures S2 and S4, this relationship is validated using lagged correlation, at a very high value of 0.95. It is however not assumed in our Fig. 2, which is entirely empirical.
The theoretical result in Method suggests that the slope of the linear line is -T/σ22, where σ2 is the standard deviation of the R(t) profile. In general, the slope can be different for different regions with different levels of quarantine and epidemic characteristics. The hospital treatment efficacy would influence T directly, as we also found. The effect of quarantine would influence the value of σ1, the standard deviation of the newly infected, and so indirectly R(t) and σ2. Our empirical result from Fig. 2 however shows that the slope is the almost the same for different regions in China, implying that efficacy of treatment and level of quarantine affect T and σ2 proportionally.
Predictability
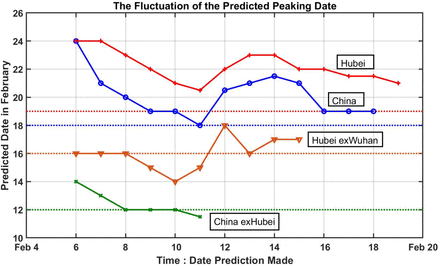
Since the logarithm of NR lies on a straight line passing through the turning point of EIC, it would be interesting to explore if the turning point can be predicted by extrapolation using data weeks before it happened (see Figure S1). How far in advance this can be done appears to be limited by the poor quality of the initial data. Fig. 3 shows the results of such predictions (See Method). The horizontal axis indicates the last date of the data used in the prediction. The beginning date of the data used is 24 January for all experiments. Prior to that day, data quality was poor and the newly recovered number was zero in some days, giving an infinite NR ratio.
Prediction of the turning point in EIC by extrapolating the trend in logarithm of NR (see Method). The horizontal axis indicates the date the prediction is made using data prior to that date. The vertical axis gives the dates of the predicted turning point. Dashed horizontal lines indicated the true dates for the turning point, as determined from Fig. 1.
For China outside Hubei, the prediction made on 6 February gives the turning point as 14 February, two days later than the truth. A prediction made on 8 February already converged to the truth of 12 February, and stays near the truth, differing by no more than fractions of a day with more data.
The huge data glitch on 12 February in Hubei affected the prediction for Hubei, for China as whole, and for Hubei-exWuhan. These three curves all show a bump up starting 12 February, as the slope of N(t) is artificially lifted. Ironically, predictions made earlier than 12 February are actually better. For example, for China as a whole, predictions made on 9 February and 10 February both give 19 February as the turning point, only one day off the truth of 18 February. A prediction made on 11 February actually gives the correct turning point that would occur one week later.
At the time these predictions are made, the newly infected cases were rising rapidly, by over 2,000 each day, and later by over 14,000. It would have been incredulous if one were to announce at that time that the epidemic would turn the corner a week later.
Even with the huge spike for the regions affected by the Hubei’s changing of diagnosis criteria, because of its short duration the artifact affects the predicted value by no more than 3 days, and the prediction accuracy soon recovers for China as a whole. For Hubei, the prediction never converges to the true value, but the over-prediction is only 2 days. This smallness of the error is remarkable given that other model predictions differ by weeks or months.
Table S1 lists the mean and standard deviation of the predictions. For applications to other countries and to future epidemics without a change in the definition of the “infection” to such a large extent, we expect even better prediction accuracy.
Inferring statistical characteristics of the epidemic
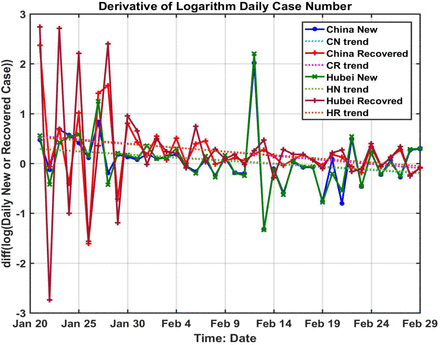
Interestingly, the derivative of log N(t) or log R(t) also lies on a straight line, as shown in Fig. 4 (although the scatter is larger as to be expected for any differentiation of empirical data). The positive and negative outliers one day before and after 12 Feb are caused by the spike up and then down, with little effect on the fitted linear trend (but increases its variance and therefore uncertainty). Moreover, the straight line extends without appreciable change in slope beyond the peak of N(t), suggesting that the distribution of the newly infected number is approximately Gaussian. For an exponential function, the derivative of its logarithm being a linear function of time is highly suggestive of a general type of distribution including Gaussian and Rayleigh. The recovery time T can be determined as t1-t0, where t1 is the peak of R(t) and t0 is the peak of N(t). These two peak times can be obtained by extending the straight line in Fig. 4 to intersect the zero line. This predicted result can be verified statistically after the fact by the lagged correlation of R(t) and N(t). If the distribution is indeed Gaussian or even approximately so, the slope in Fig. 4 would be proportional to the reciprocal of the square of its standard deviation, σ, as:
The derivative of the logarithm of daily newly infected or recovered. Notice the clear separation of the new and recovered cases and also the subtle difference of their slopes. The zero crossings of the trend line give the peak dates of the new and recovered case respectively. And the slopes give an estimate of σ values. In this Figure, the following abbreviations are used: C=China; H=Hubei; N=New Case; R=Recovered.
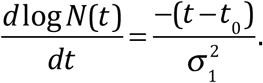
Similarly result holds for the daily number of recovered, R(t).
The inferred statistical characteristics of the Covid-19 epidemic are summarized in Table S2 for various regions. The mean recovery time T, is about 13 days for China as a whole. For Wuhan, the city at the epicenter whose hospitals were more overwhelmed and the patients admitted into hospitals more seriously ill than those in other provinces, T ∼16 days, while that for Hubei is 14 days. The standard deviation, σ, is found to be around 8 days, with slight difference between that for N(t) and for R(t), with one exception for Hubei outside Wuhan. Such a fine subdivision may not be practical for the data quality we have. The σ tends to be smaller for China as a whole than Wuhan. One can see that T and σ2 indeed varying approximately in proportion.
Estimate of “all clear” declaration
We can now estimate a time for a declaration of “all clear”. No verification is yet possible as the predicted date has not occurred. At the turning point, the EIC is still at its peak. For the disease to have run its course, and an “all clear” declaration can be announced, we require that the newly infected case number to drop to zero, for prediction practice measured by three standard deviations from the peak of N(t). Then we wait for two incubation periods, each 14 days, to pass, before we declare “all clear”. Using the inferred disease characteristics in Table S1, our prediction is, for China outside Hubei: the last week of March. For China as a whole: the first week of April, barring “imports” of infected from abroad. At this point there may still be some patients in the hospital who are infected with the virus. The “all clear” call assumes that these patients are not roaming freely to cause new infections.
South Korea
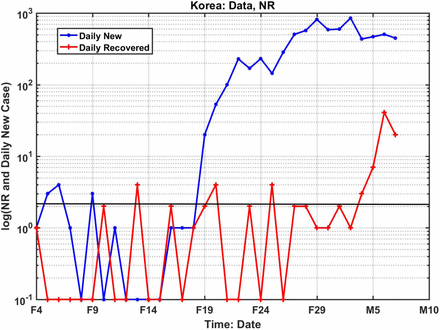
Finally, we apply the present approach the still expanding outbreak in South Korea, with very limited data. We estimate that the turning point for EIC is on March 11. See Method. An estimate of the end of the epidemic can be given as the second week of April, using the estimated value for t0= 3 March, σ=4.5 days. Remarkably, this date is around the same time as for Wuhan, China. South Korea owes its quick turning point and end of the epidemic date to its ability to identity the first infection and the secondary infections at Shincheonji Church (31), where most of the infected were concentrated. This is reflected in the data: σ for South Korea is only half that of China, with a more rapid rise and fall of the newly infected. Its data for the newly infected are probably more accurate compared to other countries in similar stage of the epidemic, due to its massive and speedy (within 6 hours) testing of the population in its “trace, test and treat” policy.
Conclusion
We offer an alternative data-driven approach to track and predict the course of the epidemic. Many parameters characterizing an epidemic can be determined from local-in-time data. Validated by real data, we suggest that our approach could be applied not just to the current Covid-19 epidemic, but also generally to future epidemics of low fatality rates. It could also be used as a practical tool for epidemic management decisions such as quarantine institution and medical resource planning and allocations (32-35).
METHOD
Theoretical support
The NR ratio is defined as:
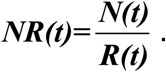
For an epidemic like COVID-19, where the case fatality rate is low (at around 1%), most of the infected would eventually recover; therefore, we have, as will be verified later:
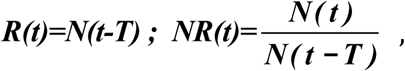 where T is the hospital stay period before recovery, with its value governed by the efficacy of the treatment. Using real data, we show that this ratio follows a straight-line trend. To explain this intriguing feature, we find theoretical support based on Gaussian distributions for the daily new and recovered case numbers. Gaussian distribution is a simple and reasonable form for a distribution that has a single peak, with rapid rise, plateauing near the peak and then declining rapidly. Later, we will verify using actual data for China that they are indeed very close to Gaussian.
where T is the hospital stay period before recovery, with its value governed by the efficacy of the treatment. Using real data, we show that this ratio follows a straight-line trend. To explain this intriguing feature, we find theoretical support based on Gaussian distributions for the daily new and recovered case numbers. Gaussian distribution is a simple and reasonable form for a distribution that has a single peak, with rapid rise, plateauing near the peak and then declining rapidly. Later, we will verify using actual data for China that they are indeed very close to Gaussian.
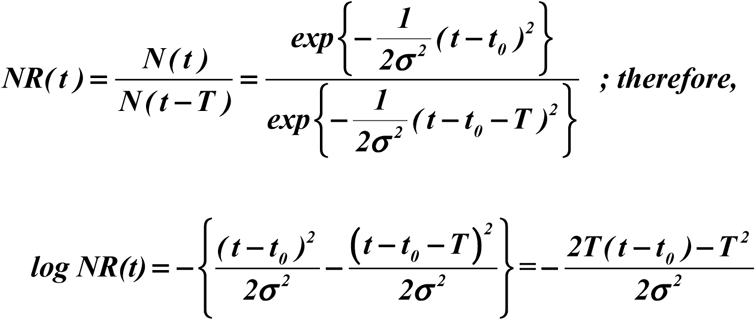 a linear function of t. The intercept with 0 yields
a linear function of t. The intercept with 0 yields 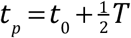 .
.
In reality, the distribution is only approximately Gaussian, of course. But the approximation is very close for the central part of the distribution near the peak. In fact, central limit theory would favor a Gaussian distribution when the data base is large.
Empirically, we find that the σ value for N(t) and R(t) are close to each other but slight differences exist, as shown in Table S2. This is to be expected, for even though the new and recovered case happen in tandem with former leading the latter, the hospital treatment and stay constitute effectively a smoothing filter on N(t) to produce R(t). The hospital process tends to spread the R(t) distribution wider, thus yield a slightly larger σ values. Given the scatter of the differentiation done for Figure 4 to infer individual distribution characteristics, the difference may or may not be significant. More data from various regions under different conditions may resolve this problem in the future. Taking this difference into account the form of real NR should be modified to be:
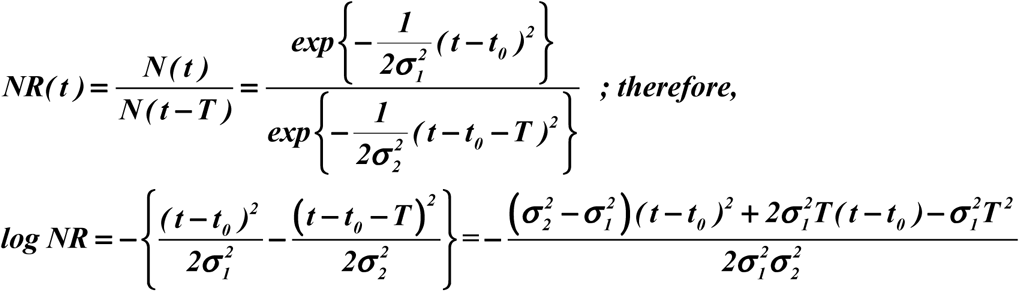
As the values of σ1 and σ2 are very close based on the empirical data, the quadratic term is always small comparing to the other terms for the length of time we are considering here. Hence.
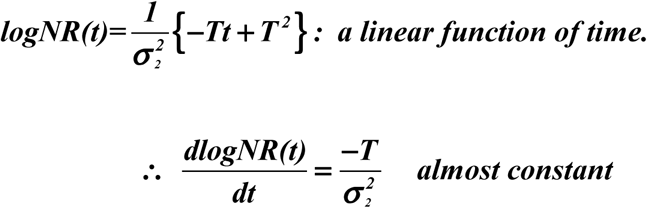
The turning point is still determined by log NR=0, yielding a theoretical value of tp=t0+T /2. This theoretical value can be used when the data on R(t) is not available.
If the daily data is indeed near Gaussian, then for the daily newly infected cases, we should have approximately,
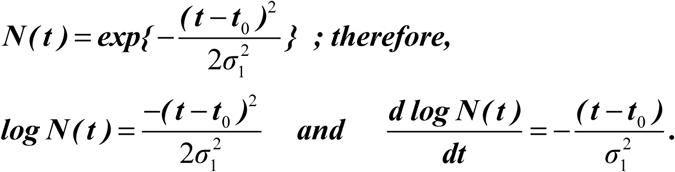
The same is true for the recovered cases, except with t1 replacing t0 and σ 2 replacing σ 1.
Importantly, the real data indeed validate a near-straight line function for NR throughout all phase of the epidemic, and the near-Gaussian distributions for both N(t) and R(t). Straight line functions are easy to extend and making predictions easy and robust. These properties also enable us to infer many of the key statistical characteristics of the epidemic from empirical data, such as the turning point, peaking times t0 and t1 and the σ of the distributions from the formulas given above.
There are some subtle points that need to be discussed further. Comparing the NR ratio approach and the derivative of individual distribution approach, we can see that the NR ratio is much smoother; however, the derivative of individual distribution is richer in information for predicting the ‘all clear’ time shown later.
Validation
a. Lagged correlation
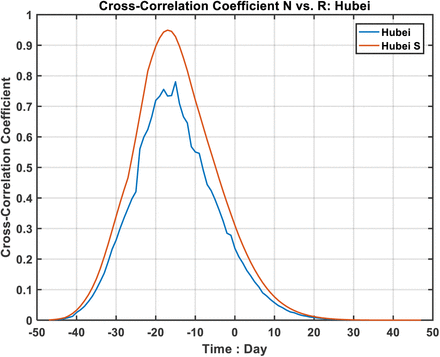
First, we validate statistically using lagged correlation between N(t) and R(t) the relationship between the two. Figures S2 and S4 show that they are highly correlated: with correlation coefficient of 0.95 when both distributions are smoothed with 5-point box car. The unsmoothed daily data also yield a high correlation coefficient of 0.80, with R(t) lags N(t) by T∼15 days. Both of the correlation coefficients are statistically significant. The result on T is consistent with that estimated or predicted using the slope of the distribution in Figure 4. The latter, obtained by the intercept of the straight line, is less accurate because of the slope is rather shallow.
b. Gaussian distribution
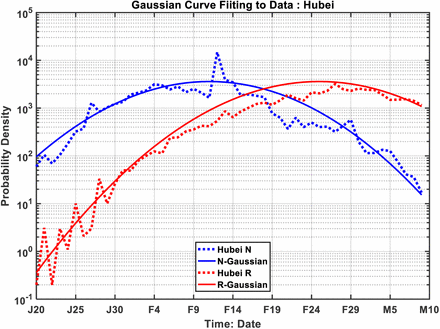
A Gaussian distribution is completely characterized by the location of the peak and the standard deviation. These quantities are determined from the slopes in Figure 4, and therefore there are no free parameters. Even without the use of disposable parameters, the fit of Gaussian to the actual distribution is adequate, as can be seen in Figure S3. The corresponding correlation and Gaussian fits for Hubei province are given in Figures S4 and S5.
c. EIC
EIC is the accumulated newly infected minus the accumulated recovered. Given the result in a, a simpler calculation can be performed which avoids the early poor data:
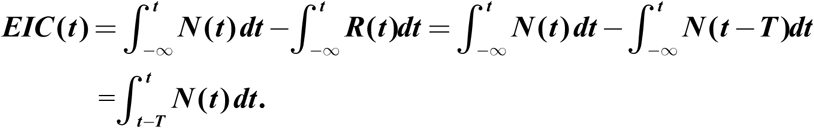
That is, to find EIC at time t, one only needs to add up the daily newly infected case numbers for a period of T preceding t. This is an almost local-in-time property even for this accumulated quantity. For validation, we estimate the peak of the EIC number on 18 February by computing the sum of daily newly infected case numbers for 15 days, from February 4 to February 18, which yields an EIC on 18 February of 54,747. This is within 10% of the actual number of 57, 805, even after taking into account the deaths (by subtracting the accumulated deaths of 2,004 from our estimate).
Estimating the end date of the epidemic
From the σ and T numbers, one can make predictions on the end of the epidemic as follows. There are two different definitions:\
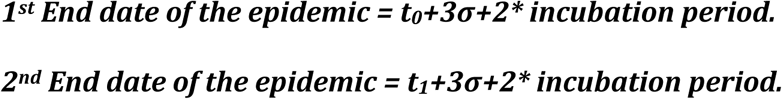
The first one depends on the newly infected case, the second one, on the daily cured cases. If we take the incubation time as 14 days, the end of the epidemic outbreak can be calculated easily from the data given in Table S1. Based on our analysis, Wuhan would come out of the epidemic the latest, long after the rest of the country, at around

The estimate based on the first definition is reported in the main text..
South Korea
Finally, we will show how this method is applied to the expanding outbreak in South Korea. Figure S6 summarized the available data at the present. The recovered case numbers hovered around 1 and 2 daily up to March 1st. It only picked up toward the end. Starting from 19 February, there seems to be enough new daily infected cases. All these phenomena are not random events, for the South Korea Government has identified that the epic center of the epidemic is at church gathering in the city of Daegu and North Gyeongsang province, where 90% of the cases are found. Specifically, a confirmed COVID-19 patient was reported to have attend the Shincheonji Church of Jesus services twice on February 9th and 16th. Given the incubation period of 7 to 14 days, the initial explosion at February 19th and the first peak value around February 24th are not accidents.
If we use the available daily new cases data, we can get the statistical characteristics of the distribution of the daily new cases from Figure S7, which gives the t0 as March 3rd and a σ value of 4.5 days. If we further use the turning point as approximately t0+T/2, then the turning point should fall on March 10, assuming T as 14 days based on the over all mean from different regions in China.
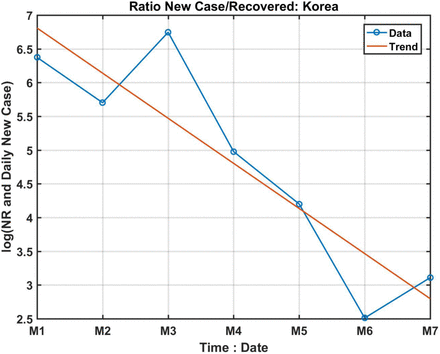
For the NR ratio, it is limited by the availability of recovered case number. If we use the limited recovered cases starting from March 1st, we have 7 days of data. The computed the NR ratio together with the trend is given in Figure S8. The turning point, at the zero-crossing of the extended trend line, would occur between March 11th and 12th. This approach does not need to use a value for T.
It should be pointed out that the Korean data available is only marginal. The predicted date of turning point by NR ratio would be between March 11th and 12th; by the derivative of distribution it would be March 10th. The result is not only consistent, but also validated by real data showing the turning point on March 12th, a pleasant surprise.
Data Availability
All data used in this study are publicly available.
Competing Interests
The authors declare no competing interests.
Data Availability
All data in this study are publicly available from World Health Organization (WHO) at https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/ and on the Daily Brief site of the China’s National Health Commission at http://en.nhc.gov.cn/
The Korean data is available at https://sa.sogou.com/new-weball/page/sgs/epidemic
Coronavirus COVID-19 Global Cases by Johns Hopkins CSSE https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6
Supplementary Information
Prediction of the turning point of EIC using linear least-squares trends using various data lengths for China exHubei. All data used start from 24 January. Different colored straight lines show the linear trend calculated from 24 January to a particular date. The spread is over a very small range. Then these trends are extrapolated (extrapolations not shown) to intersect the zero line to yield a prediction for the turning point. The blue dots are the data.
Lagged correlation of R(t) with N(t) for China as a whole.
Gaussian fit of N(t) and R(t), for China as a whole.
Lagged correlation of R(t) with N(t) for Hubei province.
Gaussian fit of N(t) and R(t), for Hubei Province.
Predicted turning point dates. Shown are the mean and standard deviation of the predictions over the prediction period, using the NR ratio method
Statistical characteristics of the COVID-19 epidemic in different regions in China inferred from data, for N(t), the daily number of newly infected and for R(t), the daily number of recovered.
The available data from South Korea (as of March 7th). The sporadic recovered case numbers are mostly in the single digit. If we use the sudden increase of recovered case matching with the sudden explosive increase of new infected, the distance is approximately 14 days, a reasonable T value when compared to the mean value in China. For our data analysis, we used daily newly cases starting February 19th, for the derivative of individual distribution study; we used data case from March 1st, for the NR ratio study, in order to have enough recovered cases.
The derivative of the logarithmic value of daily new infected case distribution.
The NR ratio from 7 days of data from March 1st to 7th. The estimated zero-crossing time would occur between March 11th and 12th, a value consistent with the statistics from the daily new case distribution on March 10th.
Acknowledgements
NEH and FQ are supported by the National Natural Science Foundation of China under Grant 41821004. KKT’s research is supported by the Frederic and Julia Wan Endowed Professorship.