Abstract
In March 2020, Coronavirus Disease 2019 originating from Wuhan, China, has become pandemic. Based on epidemic data from China we constructed and constrained a simple Susceptible–Infected– Infectious–Excluded (SIIE) model. The model is characterized by only three parameters: average incubation period, contact rate rC, and exclusion rate rE. These two rates control the daily multiplication coefficient β describing epidemic growth in its early exponential phase, during which the number of excluded (confirmed) individuals grows as E = E0 exp(α t) with α = ln β. The rates can be modified by non-therapeutic interventions: rC can be reduced by quarantine, while rE can be increased by efficient testing, enabling isolation of infectious individuals. In order to contain exponential epidemic growth, quotient rC/rE has to be reduced to 1. Based on the model, we estimate that the quarantine imposed in China on January 23, 2020 resulted in about 50-fold reduction of this quotient, allowing to terminate the exponential growth phase and enter the phase of exponential regression of daily new cases. In contrast, quarantine imposed in northern, most affected, Italian provinces on February 21 resulted in about 3-fold reduction of rC/rE and corresponding decrease of β from about 1.5 to about 1.2; further 5-fold reduction is necessary to terminate exponential growth. Even higher reduction should take place in France, Germany and Spain for which β > 1.3 (as of March 10, 2020). Considering longer-term dynamics in the case when the initial exponential growth is not contained by quarantine, we analyzed a scenario in which rE decreases in response to the surge of daily new cases which convinces people to isolate themselves. In such case, initial abrupt epidemic growth is followed by a slow decrease over years. This scenario, although economically and socially devastating, grants time to develop, produce, and distribute vaccine.
INTRODUCTION
On March 11, 2020 the World Health Organization (WHO) declared Coronavirus Disease 2019 (COVID-19) a pandemic. The disease is caused by a novel coronavirus, SARS-CoV-2, that is transmitted between people via respiratory droplets. Typical symptoms are fever, cough, and shortness of breath. In severe cases, infection leads to pneumonia and acute respiratory distress syndrome. There is currently no vaccine or specific antiviral treatment. The virus was first reported in Wuhan, Hubei, China, in December 2019. The disease had spread widely over the province of Hubei, but was contained as a result of a strict quarantine imposed on January 23, 2020. The peak of daily confirmed cases of about 4000 was reached on March 3, 2020, ten days after the quarantine had been imposed, and then it decreased below 100 daily new cases as observed in the beginning of March, 2020. Currently (March 12, 2020), despite some efforts, nearly exponential growth is observed in European countries, including Italy (with more than 15 000 cumulative cases), France, Germany, and Spain, recording more than 2000 cumulative cases each, and in the US with more than 1000 cases. In contrast, South Korea, having nearly 8000 cumulative cases, appears to be exiting the exponential phase due to the effective contact tracing and extensive testing.
In order to interpret data from China, Korea, Europe, and the US, we developed a simple Susceptible–Infected– Infectious–Excluded model. The model has only 3 parameters: average incubation period (known to be approximately 5 days [1, 2]) and two parameters that can be modified by applied protective measures: the contact rate and the exclusion rate. The quarantine reduces the contact rate, while testing increases the exclusion rate at which infectious individuals are put under treatment or isolated. The model is then applied to estimate the fold change of ratio of the contact rate to the exclusion rate required to contain the epidemic. The proposed model allows also to put forward longer-term scenarios, assuming either constant or varied contact rate.
RESULTS
Model
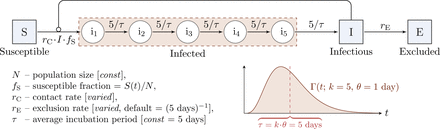
We consider the Susceptible–Infected–Infectious– Excluded (SIIE) model shown in Fig. 1, that is similar to a commonly used SIR model [3]. Our model assumes that an individual can be in one of the following states: susceptible (S), infected (i1, …, i5), infectious (I), or excluded (E). Susceptible individuals get infected by contact with infectious individuals with the rate proportional to the contact rate, rC. Multiple infected states are introduced to account for the average incubation period, τ. With k = 5 infected states such representation is equivalent to the assumption that the incubation period is distributed according to Γ(t; k = 5, θ = τ/k). Infectious individuals may become excluded with the exclusion rate rE. Excluded individuals include the confirmed cases currently handled by the healthcare system, those recovered with acquired resistance, and the deceased. Excluded individuals cannot infect. As we are interested in relatively short-term dynamics, we assume that excluded individuals maintain resistance to the disease. The dynamics is governed by the system of 8 differential equations provided and analyzed in Methods.
The incubation period, resulting from inclusion of k = 5 five intermediate infected states follows the □ distribution with average τ = 5 days, in agreement with data [1, 2]. The model is fully characterized by three parameters: rC, rE, and τ.
The exponential phase of the epidemic growth, in which the number of excluded (confirmed) individuals grows as E = E(t = 0) × exp(αt), can be analyzed based on an implicit formula following from Eq. (6) (derived in Methods):
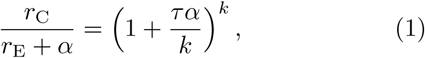 which with the number of intermediate steps k → ∞ can be replaced by
which with the number of intermediate steps k → ∞ can be replaced by

Dynamics of infection spread with respect to the contact rate and the exclusion rate
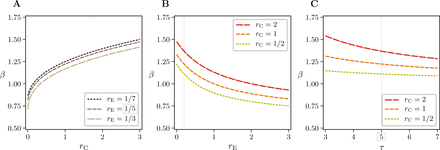
We use Eq. (1) to calculate the dependence of daily multiplication coefficient β = exp(α) on rC, rE, and τ (Fig. 2). Either a decrease of the contact rate rC or increase of the exclusion rate rE may result in reduction of β below 1 and containment of the epidemic. Practically, the contact rate is reduced by quarantine or by isolation of individuals, that both lower the potential number of contacts per individual per day, while the exclusion rate is increased by performing more diagnostic tests, that reduces the expected time for which an infected individual may infect others. Figure 2C shows also that β decreases with increasing the average incubation time, but this parameter is not controllable by protective measures.
(A) contact rate, rC, (B) exclusion rate, rE, and (C) average incubation period, τ. Default parameter vales are marked with dotted rectangles.
Equations (1) and (2) imply that
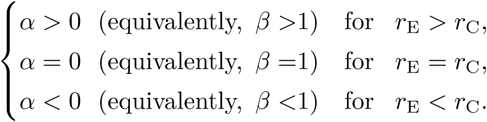
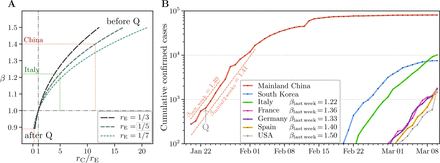
Although the daily multiplication coefficient β is not solely a function of quotient rC/rE, reduction of this quotient to 1 is equivalent to reducing β to 1, and thus containment of the epidemic. In Fig. 3A we show β(rC/rE) for three values of rE: 1/3, 1/5, and 1/7. Based on the plot for the default value of rE = 1/5, the epidemic data from China (Fig. 3B) can be interpreted as follows. Initially, the ratio rC/rE = 11.5, which corresponds to βinit(rC/rE) = 1.4 estimated for the exponential phase (Fig. 3B). Thus, to stabilize the epidemic, China had to reduce rC/rE to 1, i.e., by a factor 11.5. However as indicated by the regression of daily cases, China reduced β to approximately 0.88 = βR, which implies rC/rE = 0.22. It should be noticed that as long as the epidemic progresses exponentially, coefficient β calculated from the increase of cumulative cases E(t), and coefficient β calculated based on daily cases, E(t) − E(t − 1 day), should be equal (which can be obscured by unavoidable fluctuations in daily data). However, when the epidemic ceases, β calculated based on E(t) reaches 1, while βR based on E(t) − E(t − 1 day) becomes smaller than 1, reflecting the exponential regression of the daily as well as the active cases. Reduction of β from the initial value βinit = 1.4 to βR = 0.88 implies reduction of quotient rC/rE form 11.5 to 0.22, i.e., about 50 times. We expect that in the case of China the decrease of coefficient rC/rE resulted mainly from very strict quarantine, in which more than 50 million people in the most affected province of Hubei were forced to remain at home, with one person per household allowed to leave every few days. The 10-day time lag between introduction of the quarantine and the time of the peak number of daily new cases can be attributed to: (1) the incubation period that causes that infected individuals are registered about 5 days after infection and (2) the fact that the quarantine does not prevent mixing of infectious and susceptible individuals in households, adding next 5 days to the onset of the disease among family members. Unfortunately, this implies that even if strict quarantine is applied immediately, in European countries it will have a delayed effect.
(A) Dependence of the daily multiplication coefficient, β, on the ratio of contact vs. exclusion rate, rC/rE. Dotted lines guide the eye to relate rC/rE quotient with β coming from data for China before and after quarantine (marked with ‘Q’) and for Italy in the last week. (B) Epidemic dynamics in selected countries with high number of cumulative cases of COVID-19 based on data from Johns Hopkins University [4]. Value of βinit for China is estimated based on 7 or 14 days of early exponential phase; current β is estimated for countries being in the exponential phase based on last-week data (7 days from March 4 to March 10, 2020).
In the case of Italy, the soft quarantine imposed on Feb 21, 2020 in the most affected Italian province, Lombardy, allowed to reduce β from the initial value βinit = 1.5 (calculated based on the week February 23–29, 2020) to the current value calculated based on the last week (March 4–10, 2020) βlast week = 1.22. This implies reduction of rC/rE from about 17 to 5, i.e., only about 3.5 times. To just contain the epidemic, that is, reduce β to 1 and stabilize the number of daily cases, Italy should further reduce the contact rate 5-fold. Figure 3A indicates that 3 other European countries (Germany, France, and Spain) having more than 2000 cases and βlast week > 1.3, to contain the epidemic, should reduce the contact rate by a factor of at least 7. According to available data, a more severe situation appears to be in the US, where the value of βlast week = 1.5, which requires at least 17-fold reduction of the contact rate in order to achieve epidemic containment.
A much different dynamics can be observed in South Korea, which is exiting from the exponential phase (Fig. 3B). Among many preventive countermeasures, until March 10 South Korea performed 3.5 times more tests than Italy (210 000 vs 60 000) [5], likely substantially increasing the exclusion rate. The example of Korea is promising as it suggests that development of easily accessible, fast, and accurate tests may help to contain the spread of the disease.
Hypothetical long-term scenarios
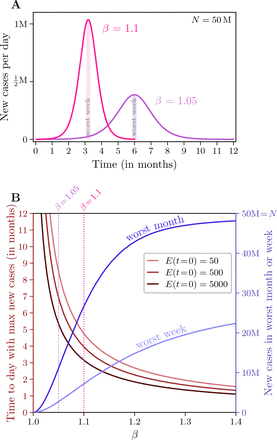
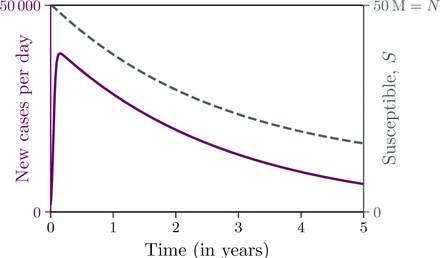
The epidemiological situation in Europe and the US may suggest that the epidemic will not be contained soon. In the long term, the cumulative number of excluded cases, E, becomes comparable to population size, N, substantially decreasing the susceptible fraction, fS, over time. As a result, the initial exponential growth ceases and the number of daily new cases reaches its maximum (Fig. 4A).
(A) Daily new cases for two values of the initial daily multiplication coefficient, β. (B) New cases in the worst week and month and time to the worst day for three initial numbers of confirmed cases. In both panels, population size N = 50 million.
The maximum number of new daily cases is higher for higher initial β, exceeding 0.3 million daily new cases for β = 1.05 and 1 million cases for β = 1.1 in the population of N = 50 million people. It is clear that even this smaller number exceeds the healthcare capacity of a country of tens of millions inhabitants such as Italy (∼60 million) or Poland (∼40 million). This, in turn, implies higher case fatality rate, which may approach the rate of severe cases (10–15% [6]). Correspondingly, with β changing from 1.05 to 1.1, time to reach the maximum daily new cases shortens twice: from 6 to 3 months, assuming the initial number of excluded (confirmed) cases, E(t = 0), equal 5000. We should notice that β = 1.05 as well as β = 1.1 require quarantine; in non-quarantined countries, such as currently France, German, Spain, and the US, parameter β exceeds 1.3 (Fig. 3B).
In Fig. 4B, we simultaneously show the number of the maximum weekly and monthly new cases and the time to reach the maximum. Parameter β > 1.1 implies that within one (worst) month more than half of population will be infected, whereas β < 1.1 require long-term quarantine.
Heretofore, we assumed that both the contact and exclusion rates, rC and rE, remain constant during the epidemic spread. Initially, when the number of cases is relatively low, the only way to reduce the contact rate is the administratively-imposed quarantine. However, one could expect that when the number of daily new cases exceeds a threshold, people will begin reducing their contacts voluntarily. To account for this behavioral aspect, we assume that the contact rate is a decreasing function of daily new cases. We propose to assume that rC = rC0 × H/ (H + (daily new cases)). This simple formula implies, in particular, that when the number of daily new cases equals H, people reduce their contacts twice. It is hard to predict the value of H, as it can be possibly culture-dependent. In Fig. 5 we show long-term epidemic dynamics assuming H = 10 000. In the considered scenario, the number of daily new cases relatively quickly approaches 40 000 and then decreases slowly over years with decreasing susceptible fraction fS. Higher H would imply higher peak followed by faster decrease. The scenario depicted in Fig. 5 results in a manageable number of new cases and grants time to develop, produce, and distribute vaccine.
Population size N = 50 million, initial β = 1.22.
DISCUSSION
In this study, we proposed a Susceptible--Infected-- Infectious–Excluded model to analyze how the dynamics of the COVID-19 spread depends on the contact rate, rC, and the exclusion rate, rE—two model parameters that can be modulated by non-therapeutic interventions. The remaining model parameter is the average incubation period, assumed equal 5 days [1, 2]. A decrease of the contact rate, which can be achieved by imposing quarantine, results in a decreases of the multiplication coefficient β that describes growth of the cumulative as well as the daily new cases in the exponential phase. Coefficient β can be decreases also by an increase of the exclusion rate, which in turn depends on efficiency of the health systems. Large exclusion rate is achieved by fast identification and isolation of infectious individuals. The critical importance has the quotient rC/rE that has to be reduced to 1 in order to contain the spread of the epidemic (increase of the number of daily new cases), and reduced further below 1 in order to eliminate the disease.
We used the developed model to analyze data from China, and found that due to very strict quarantine and other preventive efforts [7] imposed in the most affected China province, Hubei, the quotient rC/rE was reduced about 50 fold (on par with the estimated reduction of transmissibility of 97–100% [8]). This allowed to reduce coefficient β from about 1.4 in the exponential growth phase to about βR = 0.9 in the regression phase, for which βR was estimated by the decrease of daily cases in the month following the peak of epidemic. In Italy, however, in response to the mild quarantine, β was reduced from about 1.5 in the early phase (February 23–29, 2020) to 1.22 observed in the last-week period (March 4–10, 2020), which corresponds to the reduction of the quotient rC/rE from about 17 to 5; thus, further 5-fold reduction is necessary to contain the exponential spread. The 3 other European countries with the number of cases exceeding 2000—France, Germany and Spain—have coefficients β exceeding 1.3 (March 4–10, 2020), which requires at least 7-fold reduction of their rC/rE quotients. Even higher β = 1.5 is suggested by data in the US (March 4–10, 2020), which requires about 17-fold reduction of rC/rE; reduction by 70 times would bring the epidemic to the regression phase with βR = 0.9, as was done in Hubei. Higher βR ∈ (0.9, 1.0) may also allow to eliminate the disease, but the required quarantine time would be much longer. Data from South Korea suggest that this country is exiting from the exponential phase. This is possibly the consequence of effective contact tracing and extensive testing: as of March 10, the number of tests exceeds 200 000, which is 3 times more than in Italy [5].
Since the current data in Europe, US, and Iran may suggest that the epidemic will not be contained in its early phase, we have analyzed longer-term scenarios. The model with the constant contact and exclusion rates predicts that even for a relatively small exponential growth phase coefficient β = 1.05, the number of daily new cases (in a 50-million population) will exceed 0.3 million, well above the capacity of the healthcare system. Additionally, keeping the coefficient β at this low level requires rigorous limitation of personal contacts, while the time to the peak of the epidemic would be about 6 months. One of potential consequences of exceeding capacity of healthcare system is the increase of case fatality rate due to the lack of necessary medical equipment.
At this point it is worth to comment about the WHO definition of the case fatality rate, which is the ratio of deaths to confirmed cases. This definition works well in the steady state when the number of active cases remains constant or when historical data of previous epidemics are analyzed. However, in the exponential growth phase, case fatality rate understates the real rate. When, for example, the average time between the onset of symptoms or positive test and death is just four days and β = 1.2, which implies doubling of cases within four days, the number of deaths should be divided by the number of cases recorded four days before, not by the current number. This would imply doubling of the growth rate, and this suggests that the actual case fatality rate in Italy is higher than 6.6% (827/12 465, based on WHO definition and data from March 12, 2020).
Possibly, the more realistic scenario (assuming that the epidemic is not contained in the early phase) is the one in which the contact rate varies over time. As in early cases, the contact rate may be reduced only by forcing people to remain at home; in the latter phase, when the number of daily cases exceeds a threshold, people will isolate themselves in order to reduce the risk. It is intuitive to assume that contact rate is a decreasing function of daily cases in the form rC = rC0 × H/ (H + (daily new cases)), where H is the number of daily new cases for which people decide to reduce their contacts twice. In such case the number of daily new cases reaches the value roughly proportional to H and then slowly decreases due to the decreasing fraction of susceptible individuals. Such scenario seems the most realistic and, although devastating for economy and social life, grants time to develop and administer vaccine. Obviously, the more plausible is termination of exponential growth by organized quarantine and efficient testing. Based on termination of epidemic progression in China as well as in South Korea, such scenario seems to be within reach of developed countries but requires political uneasy decision.
METHODS
Model equations
The dynamics of the system depicted in Fig. 1 is governed by the following system of 8 ordinary differential equations:

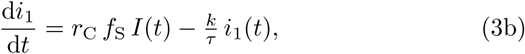
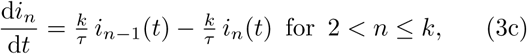


Where
 and k = 5 is the assumed number of intermediate infected states.
and k = 5 is the assumed number of intermediate infected states.
In the early phase, as long as E < N, where N = const. is the population size (with included dead cases), the susceptible fraction f = (N − E)/N ≈ 1. Under the assumption that fS = 1, the systems has the exponential solution:
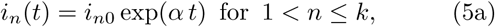

 with α satisfying
with α satisfying

When E ≪ N is not satisfied, the system becomes nonlinear, has no analytical solutions, and is solved numerically using Wolfram Mathematica (notebook is available online [9]). All numerical simulations start from an initial condition in which S(t = 0) = S0 = N − E0, in(t = 0) = in0, I(t = 0) = I0, E(t = 0) = E0, where E0 is the initial cumulative number of known cases and in0(E), I0(E), are such that the initial condition lies on the exponential trajectory.
In the model variant with varied contact rate, rC = rC0 H/ (H + (daily new cases)), daily new cases as computed as rE I(t).
It is worth noting that in the growth phase, the considered model is equivalent to the following 3-compartment model with delay τ:
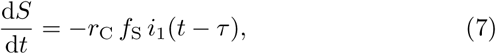
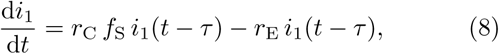

Estimation of β
Parameter β for the initial exponential growth case is estimated based on JHU data [4] of cumulative cases as:
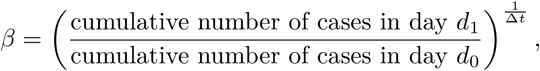 where for China day d0 is Jan 20 and day d1 is Jan 26 or Feb 02, 2020, with Δt = d1 − d0 − 1 = 6 or 13, respectively. For other countries, last-week data are used: d0 is March 4 and d1 is March 10, 2020; Δt = 6.
where for China day d0 is Jan 20 and day d1 is Jan 26 or Feb 02, 2020, with Δt = d1 − d0 − 1 = 6 or 13, respectively. For other countries, last-week data are used: d0 is March 4 and d1 is March 10, 2020; Δt = 6.
Parameter β in the epidemic regression phase in China has been estimated as the decay rate of the daily new cases in the time span from February 2 to March 2, 2020.
Data Availability
Data referred in the manuscript are available at JHU CSSE, https://systems.jhu.edu/research/ public-health/ncov, accessed: 2020-03-11 and https://www.worldometers.info/coronavirus/ covid-19-testing, accessed: 2020-03-12